unavoidable set はこんなにも複雑なのさ

　ナンプレのヒント最少個数問題には付き物の unavoidable set。
　その複雑さをちょいと紹介します。

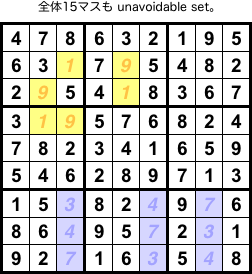
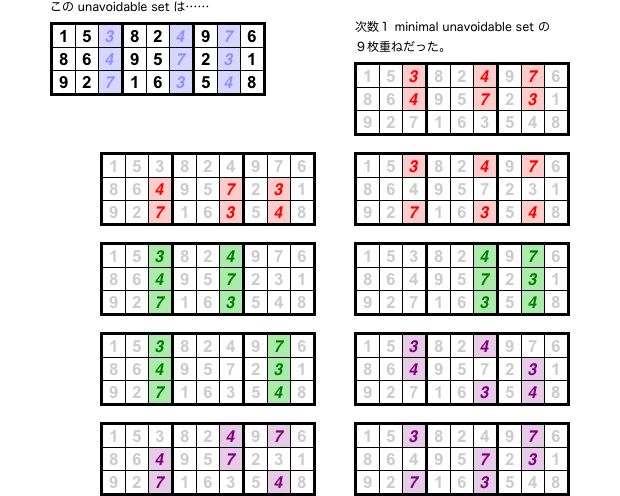
１．次数というものがある

　ナンプレが唯一解を持つためには、unavoidable set にヒント数字が必要です。
　ただ、「１個だけで良い」というわけではないのが複雑でして……。

図 1-1

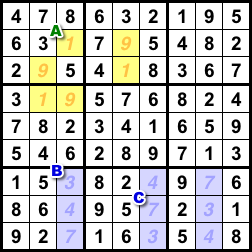
　図1-1 で説明しましょう。
　黄色 unavoidable set では、例えばマスＡの１をヒント数字にするだけで他の黄色５マスも自動的に数字が決まってくれますね。
　だから、ヒント数字１個だけで複数解を解消できます。

　しかし、青色の方は１個だけでは足りません。
　例えば、マスＢの３をヒント数字にしても、数字４と７が交換可能ですもんね。
　マスＣの７もヒント数字にして初めて複数解を解消できます。
　ヒント数字は最低２個必要なんです。

　もちろん、最低３個、最低４個、……の unavoidable set も存在します。
　必要最低個数は set によってマチマチなんですね。

　この「ヒント数字の必要最低個数」のことを 次数 といいます。
　図1-1 の黄色６マスは「次数１の unavoidable set」です。
　青色９マスは「次数２の unavoidable set」ですね。

２．minimal というものがある

　ナンプレが唯一解を持つためには、unavoidable set にヒント数字が必要です。
　ただ、「どこに置いても良い」というわけではないのがまた複雑でして……。

　minimal の定義はややこしいので、まずは次数１の minimal unavoidable set を説明しましょう。

図 2-1

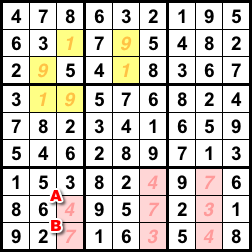
　セクション１の 図1-1 で述べた黄色６マス、これは次数１の unavoidable set でした。
　実は、この６マスにはもう１つ特徴があります。
　どの黄色１マスにヒント数字を置いても他の５マスが自動的に数字が決まり、複数解が解消されるんです。
　この「どの黄色１マスにヒント数字を置いても」が重要です。

　対して、赤色の方はちょっと違います。
　これの次数は１です。右下の赤色マスの４をヒント数字にすれば複数解が解消されますもんね。
　しかし、２マスＡ, Ｂにヒント数字を置いても、残り６マスでは未だに複数解が生じたままなんです。
　「どの赤色１マスにヒント数字を置いても複数解が解消される」というわけではないんですね。

　どの１マスにヒント数字を置いても複数解を解消できる時、その unavoidable set は minimal である といいます。
　図2-1 の黄色６マスは minimal です。
　赤色８マスは minimal ではありません。

　原論文では、「どの真部分集合も unavoidable set ではない時、（次数１の）minimal である」という定義をしています。
　これは、「これ以上マスが減ると unavoidable set ではなくなる時、minimal である」と解釈しちゃってください。
　確かに、図2-1 の黄色領域はこれ以上マスが減ると unavoidable set ではなくなります。
　minimal の意味通り、まさに「最小限の unavoidable set」と言えますね。

　次数２の場合は、次数１を使って定義します。
　こんな感じで。

　一般の場合（ｋ≧２）はこんな感じ。

　んもぅややっこしい😅
　一発でイメージしにくいですよね。
　例えば次数５を理解しようにも、４, ３, ２, １……と次数を１にまで下げてやっとイメージできますもんね。
　いやもぅ、理解するのが大変さ😞

　上記のように、１段階前の概念を用いた定義方法を再帰的定義（または帰納的定義）といいます。
　数列の漸化式などで見られる方法ですね。
　原論文ではこの定義方法を使っています。

　なお、本編のセクション4-1で定義した minimal unavoidable set は次数１の物です。
　本編では minimal unavoidable set の次数には触れていませんのでご注意ください。

３．合成したものがある

　次数、そして、minimal。
　この２つだけでも unavoidable set の複雑さが垣間見えるというもの。
　しかも、「合成できる」というんだから、それに輪をかけて複雑でして……。

図 3-1

　図1-1 をもう一度（図3-1）。
　黄色は次数１、青色は次数２の unavoidable set でした。

　この２つは個々でも unavoidable set です。
　では、黄色＋青色の15マス全体ではどうでしょうか？
　実は、それも unavoidable set なんです。
　次数は３（３＝１＋２）です。

　複数の unavoidable set を合体させても unavoidable set になるんですね。
　これが成り立つもんだから、おびただしい数の unavoidable set が完成図の中に隠れているということが想像できますね。

　まだ、図3-1 は ２つの unavoidable set が重なっていない から、例としては簡単でした。
　ところが、そうではない物もあるんです。
　図3-1 の青色 unavoidable set で説明しましょう。

　実は、この青色 unavoidable set は、次数１の minimal unavoidable set を９個も内包しているんです。
　青色は次数２でたった９マスなんだけど、「minimal の９枚重ね」というとんでもないシロモノだったわけです。

　も〜とにかく、ありとあらゆる unavoidable set を合成しちゃえば新しい物を作れてしまう。
　完成図の中に隠れている unavoidable set の個数たるや、想像を絶するものがあるんです。
　原論文によると、１つの完成図には12マス以下の次数１の minimal unavoidable set が約360個隠れているそう。
　ということは、minimal でない物も数えれば、unavoidable set の総数は……単純計算で 2360個 程度あるということになります。
　ちなみに、2360 は109桁の数です。
　１無量大数の１億倍の１億倍の１億倍の１億倍の１億倍です😅

　原論文のチームは問題解決のために次数１の minimal unavoidable set だけに注目し、一般の unavoidable set を相手にはしませんでしたが、もぅもぅもぅ当たり前だとしか言いようがない。
　2360個の処理なんて、コンピュータがパンクするどころじゃない。
　宇宙が終わってしまう！！

　……まぁ、2360個は実は冗談です😅
　盤面は81マスしかないので、マスの集合は全部で (281－1) 個しかありません（空集合を除くので１減ります）。
　unavoidable set の個数が 281－1 を超えることはないですが、まぁ、それでも想像を絶する数にはなるだろうと推測できます。
　ちなみに、281 は25桁の数です。
　もぅもぅもぅ数が多すぎちゃって、まともに相手にするのは無理でしょう😅