1.グラフとは何ぞや?
一筆書き。
まぁ、言うまでもなく有名なパズルですよね。
『ケーニヒスベルクの橋』に始まり、300年ほどの長い歴史を誇るパズルです。
中世の都市・ケーニヒスベルクにはプレーゲル川が流れ、その川を取り巻く4つの陸地には7つの橋が架かっている。
この橋たちが主人公の問題です。
数学者オイラーが解決したことで有名ですね。
ただし、どこから出発しても良い。
皆さんご存じの通り、この問題は「一筆書きは不可能」と否定的に解決されました。
一筆書きができる条件も皆さんはご存じでしょう。
- 一筆書きができる条件は「奇頂点が0個または2個存在する」である。
奇数本の線が一点に集まっている時、その点を 奇頂点 と呼びます。
偶数本なら 偶頂点 です。
奇頂点の個数がカギを握っているわけですね。
一筆書きと関わりが深い物と言えば、やっぱり数学の「グラフ理論」ですよね。
そこで、当ページではグラフ理論の視点から一筆書きを見てみようと思います。
というわけで、まずは「グラフ」という物を説明しましょう。
あ、以降の説明は当サイトの『迷路パズルでもグラフ理論が大活躍さ!』のページと同じです。
ご存じの方々は読み飛ばしてかまいません。
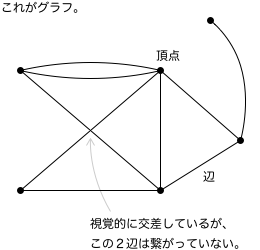
まず最初に、いくつかの点が置かれている。
そして、2つの点に繫がりがあれば線で結ばれる。繫がりがなければ線で結ばれない。
時には二重三重に線で結ばれたりする。
それらの点をいろいろと線で結んでいくと1つの構造ができあがる。
この構造を グラフ と呼びます。
グラフを構成しているものは点と線の2種類だけです。
点のことを 頂点 と呼び、線のことを 辺 と呼びます。
辺は頂点の結びつきを示す物なので、辺の両端には必ず頂点があります。
辺が繋がる時は必ず頂点を経由するので、辺同士が視覚的に交差していても「その2辺が繋がっている」ことを示しているわけではありません。
そこはご注意ください。
立体交差していると考えると良いでしょう。
『ケーニヒスベルクの橋』の地理関係をグラフで表してみましょう。
4つの陸地を頂点A〜Dとして、橋が架かっている時は2点が辺で結ばれています。
AB間が二重に結ばれているのは、AB間に橋が2本架かっているからですね。
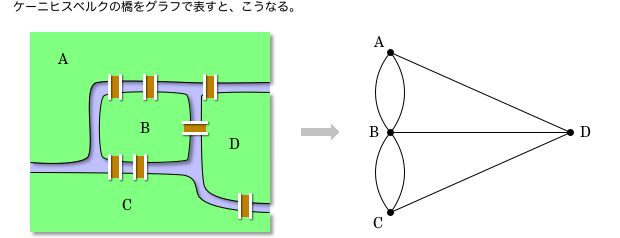
ここで、陸地や橋の形状などはまったく考慮されていないことに注意しましょう。
グラフにおいて重要なのは「各頂点の繫がり具合」、たったこれだけです。
だから、頂点や辺の視覚的な位置関係を考える必要はありません。「頂点Dは一番右にある」などの情報は無視できるんです。
もちろん、辺の形状や長さも無意味です。
陸地間の接続だけが重要なのだから、陸地は頂点で済ます。橋は辺で済ます。
余計な情報を削ぎ落とせば構造がシンプルになり、複雑な事象を把握しやすくなるんですね。
2.すべての線を通過せよ! オイラーグラフ
グラフの説明を済ませたところで、ここからは2つの視点でグラフを考察していきましょう!
「すべての辺を通る」「すべての頂点を通る」の2つです。
まずは前者から。
いわゆる「一筆書き」です。
2-1.あの法則をグラフ理論用語でおさらい
……考察と言っても、まぁ、皆さんはあの法則を既にご存じですよね😓
グラフ理論用語を交えて、その法則を軽く説明しましょう。
まず、頂点は大きく2種類に分かれます。
頂点Aから奇数本の辺が出ている時、Aを 奇頂点 と呼びます。偶数本ならAは 偶頂点 です。
こういう定義をすると、一筆書きの有名な法則はこう言い表せますね。
- グラフが一筆書きができるための条件は「グラフが奇頂点を0個または2個持つ」である。
この法則に関連して、一筆書きに関わりの深いグラフを2つ紹介しましょう。
頂点Aからスタートして、すべての辺を1回ずつたどってAに戻って来た時、そのグラフを オイラーグラフ と呼びます。
すべての辺を1回ずつたどってA以外の頂点に着いた時、そのグラフを 半オイラーグラフ と呼びます。
例えば、こんな感じ。
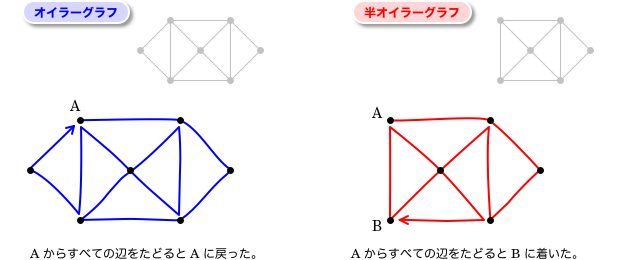
おそらく「一筆書きの法則をオイラーが証明した」ということに由来するのでしょう。実にわかりやすい用語ですよね。
奇頂点に関連して、次のことが成り立ちます。
- 奇頂点を持たないグラフはオイラーグラフである。
- 奇頂点を2個持つグラフは半オイラーグラフである。
オイラーグラフ&半オイラーグラフの2つ。
これが一筆書きのすべてです。
そういや、『ケーニヒスベルクの橋』問題のグラフはセクション1で示しましたっけ。
このグラフの奇頂点はいくつあるでしょう?
4つですね。実はすべて奇頂点です。
ということは、このグラフはオイラーグラフでも半オイラーグラフでもないわけですね。
もちろん、一筆書きは不可能です。
2-2.輪を使って一筆書きができる
さ、よく知られた法則の話はここまで。
このセクションでは、奇頂点/偶頂点 から離れて「輪」という視点で話をすることにしましょう。
オイラーグラフを対象に話をしていきます。
オイラーグラフ上のとある頂点Aから辺をたどっていくと、同じ頂点を二度通らず少し転々としてAに戻ってくることができます。
この時、その軌跡は小さな輪になっていますよね。
この輪を 閉路 と呼びます。
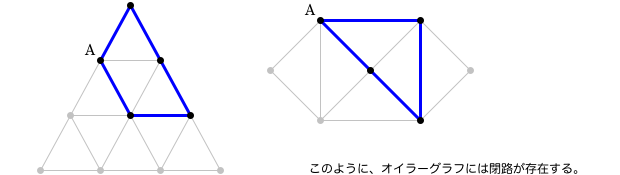
実は、閉路に関する性質がオイラーグラフにはあるんです。
こういう定理がある!
連結グラフがオイラー・グラフであるための必要十分条件は,その辺集合が互いに素な閉路に分割できることである.『グラフ理論入門 原書第4版』p.44 より
グラフ理論用語が散在していてわかりにくいので、少し大雑把に言い換えましょう。
オイラーグラフはこういうことができるんです。
- オイラーグラフは、辺を共有しない閉路に分割できる。
(頂点は共有しても良い)
例えば、下図のような感じ。
ただ、分割方法は一意ではないから、方法に応じて閉路の形と個数はさまざまです。
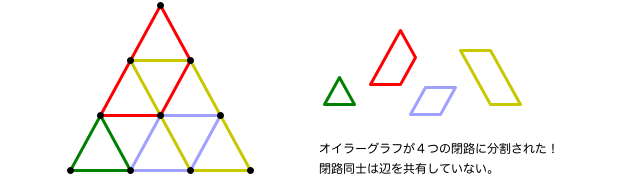
オイラーグラフは一繋がりのグラフなので、孤立した閉路はありません。
だから、分割された閉路たちは頂点をあちこち共有し合って、全体で一繋がりになっています。
その共有点を利用して、一筆書きの道筋を作れるんです。
こういう方法で。
頂点を共有している2つの閉路を融合させちゃえ〜!
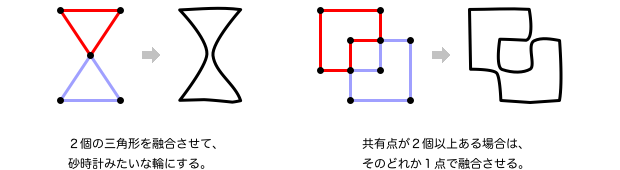
閉路を融合させると、少し大きな輪が誕生し、輪が1個減る。
輪が複数ある限り共有点は必ずどこかにあるから、その共有点で輪をどんどん融合できる。
そうすると、最終的に1つの大きな輪ができあがる。
これが、オイラーグラフをたどる道筋になっているんですね。
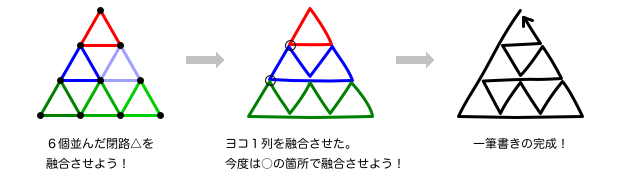
これは、一筆書きの道筋を見つける方法の1つです。
ただ……思ったけど、結構メンドウだねこれ😅
わざわざ閉路に分割してから融合させて……、と二度手間😅
ま、一筆書きにはこういうやり方もありますよ、ということで許してください😅
2-3.Fleury のアルゴリズム
お口直し。
実は、オイラーグラフを一筆書きするための確実な方法が既に存在します。
Fleury のアルゴリズム と呼ばれる方法です。
原則として、任意の頂点から出発して自由に辺をたどれば良い。
ただし、次の規則に従うこと。
《1》たどった辺は除去する。もし孤立点が生じたらそれも除去する。
《2》他にたどれる辺がある限り、橋を渡ってはいけない。
孤立点とか橋とか、またグラフ理論用語が出てきたぞ😅
それらの用語も説明しながら、実際に Fleury のアルゴリズムで一筆書きをしてみましょう。
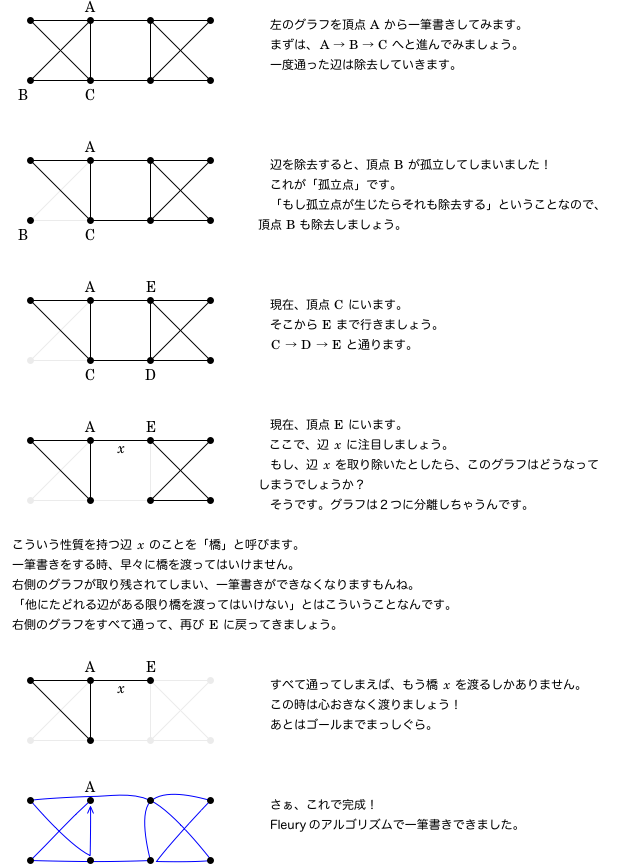
橋さえ注意していれば、Fleury のアルゴリズムは難しくありません。
一筆書き問題を解く際は、この方法を思い出してチャチャッと解いちゃってくださいね😊
2-4.一筆でダメならn筆は……?
一筆書きの法則は世の中に知れ渡っています。
しかし、当然ながら、世の中には一筆で描けない図形も山ほどあります。
じゃぁ、一筆でダメなら何筆で描けるのか?
その法則について軽く説明しましょう。
ちょいと例をいくつか挙げてみます。
下図の3つのグラフ、奇頂点はそれぞれ4個, 6個, 8個です。
それぞれ何筆で描けたかというと……2筆, 3筆, 4筆。
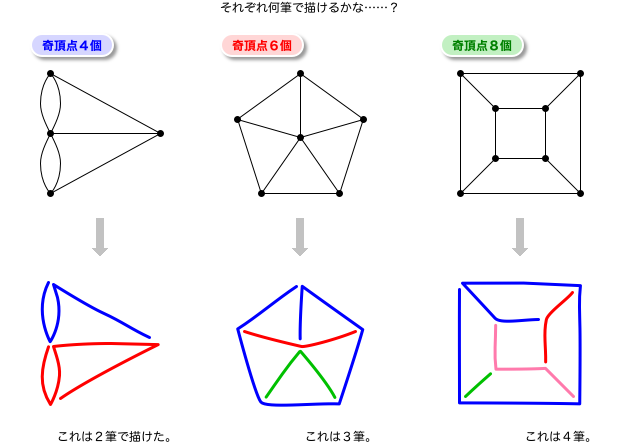
なんかもぅ、あまりにも法則がわかりやすい😅
奇頂点の半分だね!
実は、グラフと筆数の関係について簡単な定理があるんです。
逆に、グラフがn筆書き可能である時、そのグラフは奇頂点を 2n 個持っている。
奇頂点の個数 2n とn筆書き、両者は必要十分条件の関係にあるということなんですね。
あっ、どのグラフも奇頂点は必ず偶数個持っています。
奇数個はあり得ないことに注意してください。
定理が成り立つ理由を簡単に説明しましょう。
頂点の立場から一筆書きを見ると、「ペンが訪れては去って行く」と言えますね。
この「訪れる&去る」をワンセットとして頂点周りの辺を2本ずつ消費していくから、奇頂点周りの辺は最終的に1本だけ残ります。
その1本は線描の 開始/終了 にならざるを得ません。
言い換えると、奇頂点は必ず線描の 始点/終点 にならざるを得ないわけですね。
だから、奇頂点が多くなると筆数も増えていくことになります。
例えば、グラフに奇頂点6個A〜Fがあったとしましょう。
この場合、奇頂点を2個ずつペアにして「AからBへ描く」「CからDへ描く」「EからFへ描く」といった3筆が最低でも必要になるわけです。
一般の場合も同様で、奇頂点 2n 個に対してはn筆が必要になるんですね。
最少筆数で済ませるコツは、奇頂点から別の奇頂点へ一筆で描くことです。
上図のグラフは、どれもそういうふうに描いていますね。
テキトーに描いたら筆数が無駄に増えちゃうから、うまく描くようにしましょう!
3.すべての点を通過せよ! ハミルトングラフ
前セクションでは「すべての辺を通る」ことに注目してオイラーグラフの話をしましたね。
今度は「すべての頂点を通る」ことに注目してグラフを考察していきましょう!
3-1.ハミルトングラフとは何ぞや?
セクション2ではオイラーグラフと半オイラーグラフの2種類を紹介しました。
実は、ハミルトングラフも同様に2種類あります。
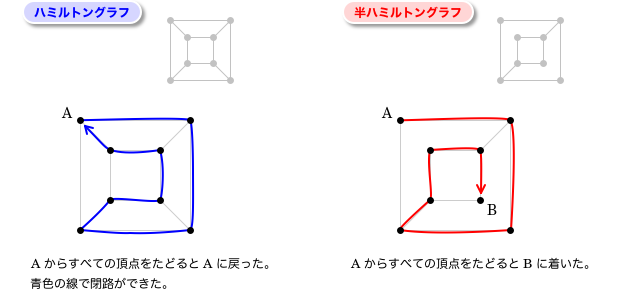
頂点Aからスタートして、すべての頂点を1回ずつたどってAに戻って来た時、そのグラフを ハミルトングラフ と呼びます。
すべての頂点をたどってA以外の頂点に着いた時、そのグラフを 半ハミルトングラフ と呼びます。
「すべての頂点を通る輪があればハミルトングラフだ」と考えるとわかりやすいかも。
セクション2-2でも説明しましたが、この輪のことを 閉路 と呼びます。
あっ、必ずしもすべての辺を通る必要はありません。
残念ながら、ハミルトングラフに関してはこれと言った法則はありません。
ものすご〜く大雑把に言うと、「十分多くの辺を持つグラフはハミルトングラフだ」というふんわりした法則はあります。
これを厳密な形にした物に「Dirac の定理」「Ore の定理」などがありますね(詳細は省略します)。
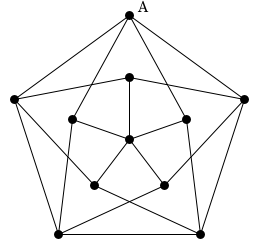
ここで、ちょいとパズル問題を1つ。
頂点Aからスタートし、すべての頂点を1回ずつ通り、再び頂点Aに戻ってくるルートを見つけられますか?
これは Grötzsch グラフ と呼ばれています。
グラフ理論の入門書ではよく紹介されているので、ご存じの方々は多いかもしれませんね。
ちなみに「グレッチ」と読むようです。
ドイツの名前は難しい😅
この問題、結構侮れませんよ〜!
お時間のある時にゆっくりじっくり考えてみてください😊
3-2.ハミルトンの世界一周の旅
ところで、ハミルトンって……誰なんでしょう?
ハミルトンとは、アイルランドの数学者ウィリアム・ローワン・ハミルトンのことです。
光学や解析力学などの分野で偉大な業績をあげ、また『四元数』の研究に心血を注いだことで有名ですね。
10歳くらいにはもう何カ国語も操っていたという、神童の中の神童。
数学でもズバ抜けた才能を発揮し、大学生ながら「ニュートンの再来」とまで言われたほどでした。
ただ、結婚生活と酒、そして四元数そのものが彼の人生に悲劇をもたらしてしまった。
悲運の人物でもあります。
ハミルトングラフの生まれたキッカケは、正十二面体でした。
頂点を20個持つ正十二面体。その20個を1回ずつ通って出発点に戻ってくるルートはあるか?
そうハミルトンは考えていたそうです。
どうやら、ハミルトンは正十二面体を実際の地球に見立てて、こんなオモチャを作っていたらしい!
1857年,ハミルトン卿は木で正12面体を作り,12面体の稜に沿ってすべての頂点(各頂点にはその時代の主要都市名が付けられていた)をちょうど1回だけ通って出発点に戻ってくる道順を求める「世界周遊ゲーム」を考案した.『ヴィジュアルでやさしい グラフへの入門』p.89 より
現物や写真画像があれば是非見てみたかったけれど、検索しても見つからず。
あぁ気になる〜😖
『数学小景』でも少し触れているので、ちょいと紹介しましょう。
(前略)ハミルトン発明の玩具の弘めの引札が、ふるっているから、紹介をしておこう。意訳すれば、次のようでもあろうか。十二面巡礼。一名、世界周遊戯。右ハ欽命愛蘭天文博士、士爵ウィリヤム・ローウェン・ハミルトンノ発明ニ係ル。饗宴席上、座興トシテ珍奇絶妙。数学研究者ノタメニハ二十元法ノ好範例。こう書くと、少し松沢式だけれども、このハミルトンはもちろん古典力学で標識として周知の、外ならぬ彼氏である。四元法の発見者は正十二面体から抽出した二十元法をほのめかしている。渺茫たる多元数論の出現した今日、それに珍奇はないが、むしろ、ロンドン、パリ、ベルリン、モスクワ、さては新京、重慶、上海等々、各国の都市二十と、その間の交通路とを、うまく選んで、五角盤を双六式にするならば、世界一周遊戯に東洋趣味が加わるではあるまいか。『数学小景』pp.56-57 より
あ〜もぅ、引札も見たくなったじゃないか〜!
ああぁ気になるぅぅ〜😖
この世界一周問題、少しだけ簡単にできます。
正十二面体の頂点・辺をそのままグラフの頂点・辺とみなし、正十二面体の構造を保ったまま平面に書き写すことができるんです。
下図のように。
この五稜郭みたいなグラフは 正十二面体グラフ と呼ばれています。
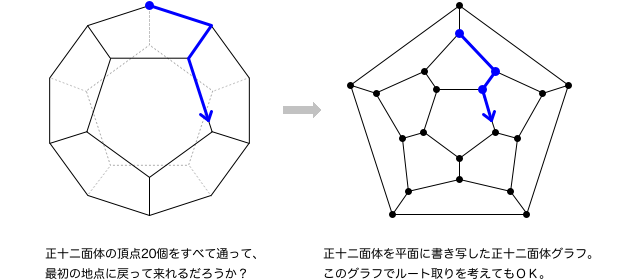
正十二面体グラフで考えると、世界一周問題はこう言い換えることができますね。
正十二面体グラフはハミルトングラフですか?
ま、すべての頂点を通る閉路は試行錯誤で簡単に見つかるので、この問題は易しいです。
ここでは、閉路の風変わりな見つけ方を1つ紹介しましょう!
『数学小景』に載っている方法です。少し端折って簡単に説明します。
正十二角形グラフって、五角形がくっつき合ってできていますよね。
ということは、その五角形たちの辺を次々たどって閉路ができるわけです。
この事実に注目しましょう!
今、五角形6個を辺でくっつけて、数珠つなぎに連ねた図形を考えます。
すると、その細長い図形は二十角形になるんですね。
それを利用して、五角形6個の数珠つなぎを正十二面体グラフから見つけよう! ……という作戦です。
さて、うまくいくんだろうか……?
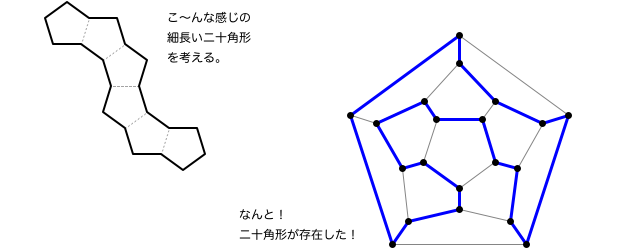
実は、うまくいくんです。
例えば、上図の通り。
無理やり「の」の字に見えないこともないガタボコ図形。もちろん、これは立派な二十角形です。
そういや、正十二面体グラフには全部で20個の頂点がありましたっけ。
そのグラフの中に二十角形が存在したわけですね。
ということは、グラフの頂点20個はすべてその二十角形の頂点にもなっていると言える。
あら、その二十角形の辺をたどってグルッと一周すれば、それが正解ルートになるじゃぁないの!
いや〜、こういう方法があったんですね〜。
辺をたどる問題なのに、面で解決できちゃう。
面白いもんですね😊
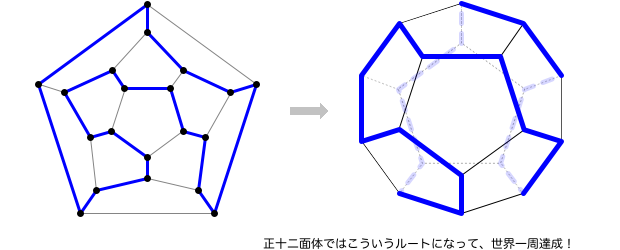
ちなみに、この6面繋ぎの閉路を正十二面体で表すと、こんな感じ。
頂点20個、見事にすべて通っていますね。
3-3.実はあの問題をオイラーが解いていた!
オイラーグラフの経緯に関しては、もぅ皆さんご存じの通りです。
一筆書きの元祖はケーニヒスベルクの橋であり、それを解決したのがオイラー。
「オイラーグラフ」の命名通り、オイラーは一筆書き界の中心人物であることに間違いありません。
さて。
そのオイラー、ハミルトングラフにも関係しているということはご存じでしょうか?
実は、とあるパズル問題もオイラーは解決したんです。
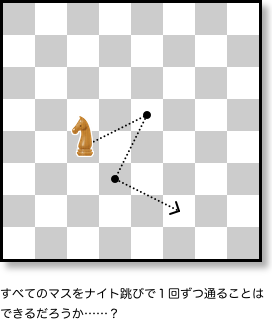
その問題とは、ナイト・ツアー。
ピョンピョン桂馬跳びするアレです。
市販のパズル本でも亜種を目にするので、このパズルをご存じの方々も多いことでしょう。
これをナイト跳び(桂馬跳び)で動かし、すべてのマスを1回ずつ訪れるルートは存在するだろうか?
このパズルを普通に解こうとするなら、「四隅からは2方向にしか行けない」ことなどに気をつけながら四隅付近からうまくルート作成していくことになるでしょうか。
ただ、なんせ64マスもあるもんだから、試行錯誤は避けられなさそう。
膨大な試行が必要かもしれない。
根気がナイトいけないね!(寒い)
オイラーはこの問題に取り組んでいました。
正解ルートは既に見つけていたものの、「任意のマスからスタートする」という条件がなかなかクリアできず悩んでいたようです。
しかし、それをエレガントな形で見事解決していた。
ちょいとその話をしましょう。
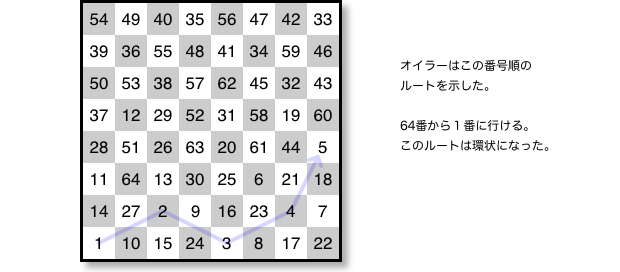
左下隅からスタートし、マスを通るたびに番号をつけていく。
下図のように 64まですべての番号が振られ、全マス通るルートが示された。
しかし、話はそれだけではなかった。
番号64から番号1へ、ナイトは跳べる。
つまり、ルートは環状にできる。
この事実がもうひとつの大きな結果を生むんです。
- どのマスからスタートしても、ナイトツアーが可能である。
なぜなら、出発点がどこであろうと番号順に跳べばいいのだから。
64番に着いたら1番に跳んで、また番号順に続ければいい。
オイラーはただルートを見つけただけではなかった。
「任意のマスからスタートする」という条件もクリアしたんです。
このたった一例だけで。
数学の証明というのは、簡潔であればあるほど美しく見える。
実にエレガントな解決方法だったことがわかります。
ちなみに、点対称の位置関係にある2マスを見てみると、法則がもう1つあります。
2マスの番号の差はどれも32になっている。
さらに磨きのかかった解決方法だった。
素晴らしいの一言でしかありません。
あっ、そういえば……。
このナイトツアー、どこら辺がハミルトングラフと関係あるんだろう?
その話をしなきゃいけませんね😅
実は、チェス盤をグラフ化させることができるんです。
こんなふうに。

なんかレースの編物が出てきたぞ😅
チェス盤のマスを頂点とし、ナイトの位置関係にある頂点同士を辺で結ぶ。
すると、こんなにも編み込まれたグラフができるんです。
このグラフにより、ナイトツアーの問題はこう言い換えることができますね。
このグラフの頂点をすべて通るルートを見つけられますか?
つまり、このグラフは半ハミルトングラフですか?
いや、もしかして、ハミルトングラフですか?
8×8サイズは既にオイラーが解決済みなので、小サイズで考えてみましょう。
3×4サイズのチェス盤を編物グラフにしてみます。
説明しやすいように、あらかじめ頂点に番号1〜12をつけておきましょう。
実は、このグラフは半ハミルトングラフではあるけれど、ハミルトングラフではありません。
その理由をこれから説明していきます。
グラフというものは、頂点同士の繫がりだけが重要です。
つまり、繫がりを勝手に変えなければ頂点の位置は本質的に関係ない。
そこで、頂点の位置をずらしましょう!
- 6番と7番を観音開きのように辺ごと左右端へ追いやる。
- 5番と8番を動かして中央を整列させる。
- 2番と10番の場所を交換、4番と12番の場所も交換する。
- あとは、テキトーに整形して完了!

まるで絡まった糸をほどくかのように、グラフをほぐしていく。
レースの編物がただの糸枠になっちゃった😅
これだけ簡素なグラフにしちゃえば、ルート探しなんて簡単です。
このグラフが半ハミルトングラフであることは明らか。蛇行ルートがありますもんね。
そして、ハミルトングラフではありません。閉路を作るには四角を描くしかないですが、5〜8番のうち2つはどうしても通れないですもんね。
3×4サイズのナイトツアー、すべてのマスを通ることは可能だけど、その上で出発点に戻ってくることは不可能なんですね。
最後に。
オイラーは8×8サイズのナイトツアーに挑んでいましたが、この問題は8×8に限った話ではありません。
他のサイズでも考えることができますね。
実は、ナイトツアーについては既に研究されていて、ツアーの可否に関して定理が存在します。
ナイト跳びですべてのマスを通る閉路を考える。
この時、次の a. b. c. のどれかに当てはまるチェス盤に閉路は存在しない。
それ以外のチェス盤には閉路が存在する。
- mもnも奇数である。
- m=1, 2, 4 のどれかである。
- m=3 であり、かつ n=4, 6, 8 のどれかである。
3×4サイズは c. に当てはまることから、ナイトツアーでは出発点に戻れないんですね。
個人的に驚いたのは、「4×nサイズはすべてダメ」というところです。
一方のサイズが4マスだと、他方がどんなに長いサイズでも閉路は絶対に作れない。
これがすごく不思議に感じました。
1つくらいはありそうなものなのにね。
魔方陣では「6×6サイズが特殊」だったように、ナイトツアーでは「サイズ4が特殊」だった。
パズルでは、こういう特定の数値に対して特殊なことがそこそこ起こる。
こういう不思議さもパズルの魅力の1つです。
参考・参照
- R.J.ウィルソン 著, 西関隆夫/西関裕子 共訳, 近代科学社,『グラフ理論入門 原書第4版』(初版第5刷), 2005
- 小林みどり 著, 共立出版,『よくわかる! グラフ理論入門』(初版1刷), 2021
- E.T.ベル 著, 田中勇/銀林浩 訳, 早川書房,『数学をつくった人びと II』(3刷), 2004
- 守屋悦朗 著, サイエンス社,『ヴィジュアルでやさしい グラフへの入門』(初版), 2016
- 高木貞治 著, 岩波書店,『数学小景』(第6刷), 2019
- P.グリッツマン/R.ブランデンベルク 著, 石田基広 訳, 丸善出版,『最短経路の本 レナのふしぎな数学の旅』(第4刷), 2021
更新履歴
- 2023. 1.27.
- 新規公開。