1.Bent Naked Subset とは何ぞや?
Bent Naked Subset を説明する前に、まずはちょびっと前準備。
舞台となる領域を紹介しましょう。
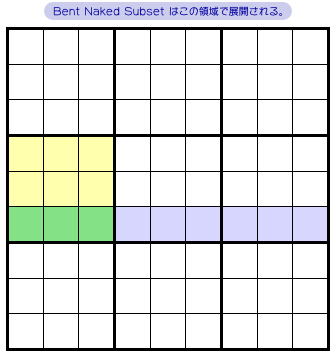
図1-1 を見てみましょう。
青色列と黄色ブロックを合成した、L字型の領域がありますね。
この領域の中で Bent Naked Subset が生まれます。
図1-1 では、青色と黄色が重なった部分を緑色で表しています。
以降は、L字型領域を青色・黄色・緑色の3つに分けて考えることにしましょう。
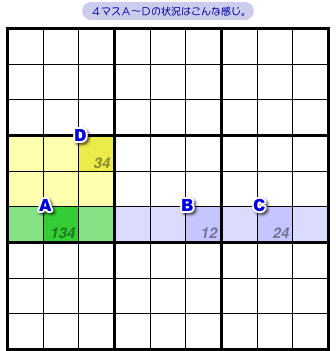
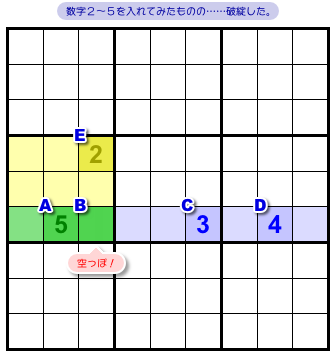
L字型領域に4マスA〜Dがあったとします。
各マスに入り得る数字は1〜4しかなく、図1-2 のようになっているとしましょう。
この4マスはこういう状況になっています。
- 最低1マスは緑色領域に属している。
- 最低1マスは青色領域に属している。
- 最低1マスは黄色領域に属している。
- 4マスA~Dにある候補数字は全部で4種類。
「4種類」と述べましたが、これは「マスの個数と同じ」と捉えてください。
n個のマスに候補数字が全n種類ある、ということです。
L字に折れ曲がった領域に4マスA〜Dが配置されている。
この4マスをひっくるめて Bent Naked Subset と呼びます。
bent は「曲がった」という意味です。
Naked Subset はn国同盟のことです。
たしかに、A〜Dは4国同盟っぽく見えますね😊
4マスだから、Bent Naked Quadruple かな?
ここで注意をひとつ。
図1-2 を見ると Bent Naked Subset はn国同盟っぽく見えますが、n国同盟ではありません。
2マスC, D両方に数字4が入る可能性があるからです。
混同しないよう、注意が必要です。
さぁ、これからこの4マスについて考察をしていきましょう!
……と言っても、まずはどこに注目すべきなんだろう?
ここに注目するんです。
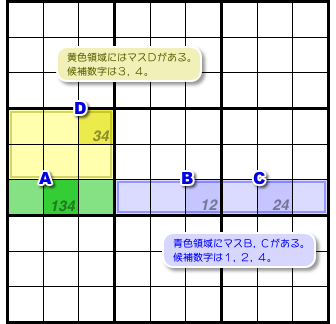
- 青色領域にあるマスと黄色領域にあるマス、両者に共通する候補数字は何種類あるのかな?
図1-3 で言うと、青色領域にあるマスはBとCの2つですね。
その中にある候補数字は1, 2, 4の全3種類。
黄色領域にあるマスはDだけですね。
その中にある候補数字は3, 4の全2種類。
候補数字4が共通していますね!
1種類ありました。
青色&黄色領域の間に共通する候補数字、いったい何種類あるのか?
その数によって、Bent Naked Subset は2つの顔を持っています。
- 共通の候補数字が1種類である Bent Naked Subset。
- 共通の候補数字が1つもない Bent Naked Subset。
両者の見た目はソックリですが、論理展開も結論も異なります。
性格のまったく違う双子みたいな感じ?
セクション23でそれぞれ解説していきましょう。
ちなみに、共通の候補数字が2種類以上あった場合は何の結論も得られません。
当ページでは省略しちゃいます😓
2.共通の候補数字が1種類である場合
まずは、共通の候補数字が1種類である Bent Naked Subset について解説しましょう。
その候補数字に関する結論が得られます。
では、解説していきましょう。
前セクションの盤面を流用しちゃいます。
手抜きとか言わないで😓
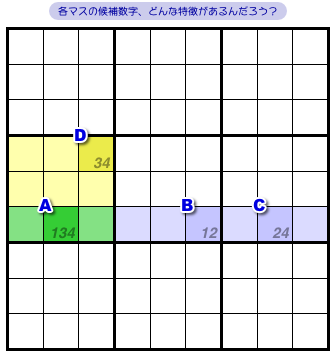
図2-1 には4マスA〜Dがありますね。
実は、この4マスには大きな特徴が潜んでいるんです。
それは何でしょう?
各候補数字の配置に特徴があるんですが……。
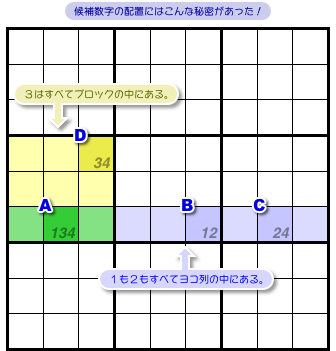
こういう特徴があるんです。
- 候補数字1はヨコ1列にのみ存在している。
- 候補数字2はヨコ1列にのみ存在している。
- 候補数字3はブロック1個にのみ存在している。
- しかし、候補数字4は列とブロック両方に存在している。
図2-2 で検証してみましょう。
候補数字1はどれも青色ヨコ列に収まっている。
候補数字2も同様。
候補数字3はどれも黄色ブロックに収まっている。
候補数字4は列&ブロック両方にまたがっている。
まさに上記の通りなんですね。
候補数字4を除いて、どの候補数字もただ1つの列またはブロックに収まっている。
図2-2 の Bent Naked Subset にはこういう特徴があるんです。
なんだか候補数字4だけがちょっと特殊ですね。
実は、この数字4に関する結論が得られます。
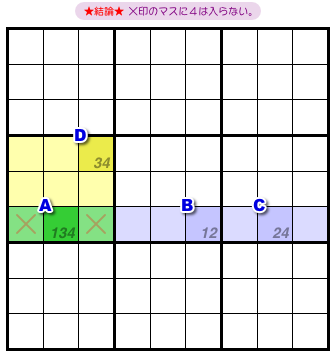
では、結論です。
- 候補数字4を持つ3マスA, C, Dすべてと列またはブロックを共有するマスがある。そのマスに数字4は入らない。
図2-3 だと、×印の2マスが該当します。
この2マスはマスA, Cと同じヨコ列に属しています。同時に、マスDと同じブロックに属しています。
この2マスに数字4は入らないというわけです。
なぜこういう結論になるのか?
それは、マスA, C, Dのどれかに必ず数字4を入れなきゃならなくなるからです。
それを解説しましょう。
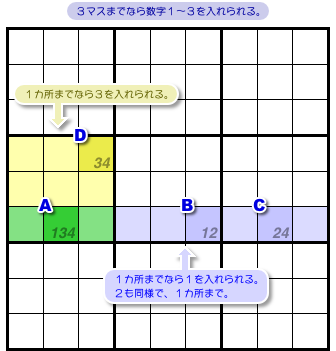
マスA〜Dに数字を入れることを考えてみましょう。
その際、成り立つことが1つあるんです。
- 数字1, 2, 3はそれぞれ1個までしか入れられない。
つまり、全部で最大3個しか入れられない。
なぜでしょう?
例えば、候補数字1はヨコ1列にしかありません。
マスAかBに数字1を入れられるけれど、1カ所に入れたらもぅ終わり。数字1は最大1カ所にしか入れられません。
数字2も3も同様で、最大1カ所にしか入れられません。
だから、3つ合わせて最大3カ所なんですね。
4マスA〜Dのうち3マスまでなら数字1〜3で埋められる。
逆に言えば、数字1〜3だけでは最大3マスしか埋まらないんです。
あらま。マスはまだ残ってるよ。
残りのマスには何を入れれば……あぁそうか、アレしかないのか!
そうです。
残りのマスには数字4を入れるしかないんです。
だって、数字1, 2, 3だけでは全然足りないんだもん!
数字4も使うしかないのさ!
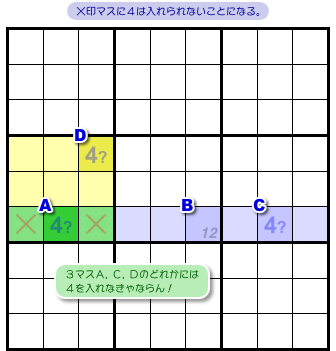
A〜Dの4マス、数字1, 2, 3だけでは埋め尽くせません。
どうしても数字4が必要になっちゃう。
というわけで、4マスA〜Dについてこういう結果になるんです。
- 4マスA〜Dのどこかに必ず数字4を入れなければならない。
実際は、マスA, C, Dに候補数字4がありますね。
ということで、「A, C, Dの少なくとも1つに数字4が入る」ことが判明しました。
そうなると、数字4を入れられないマスが生じます。
図2-4、×印の2マスです。
この2マスはマスA, Cとヨコ列を共有し、同時に、マスDとブロックを共有しています。
だから、A, C, Dのどこに数字4が入ろうとも、この2マスに4は入れられないのです。
図2-3 の結論通りですね😊
一般的な話をしましょう。
青色領域と黄色領域に共通する候補数字が1種類だけ(aとする)だった場合、次のことが成り立ちます。
- すべての候補数字aと列またはブロックを共有するマスに数字aは入らない。
これが、このセクションにおける一般的な結論です。
このセクションでは、共通の候補数字が1種類という Bent Naked Subset を紹介しました。
これは、XY-Wing 系解法を深く理解するのに役立ちます。
XY-Wing、XYZ-Wing、WXYZ-Wing、さらに VWXYZ-Wing や UVWXYZ-Wing などを一括で理解できるんです。
XY-Wing 系における本質的な概念と考えて良いでしょう。
3.共通の候補数字が1つもない場合
次は、共通の候補数字が1つもない Bent Naked Subset について解説しましょう。
前セクションより話は難しいかもしれません。
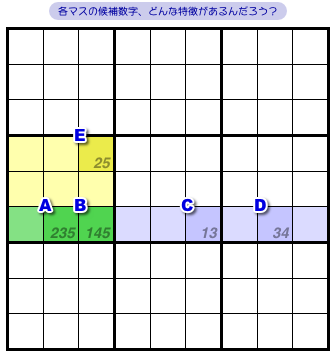
新しい盤面で解説しましょう。
図3-1 の盤面、5マスA~Eがありますね。
この5マスはこういう状況になっています。
- 最低1マスは緑色領域に属している。
- 最低1マスは青色領域に属している。
- 最低1マスは黄色領域に属している。
- 5マスA~Eにある候補数字は全部で5種類。
図1-2 でも述べましたが、「5種類」は「マスの個数と同じ」だと捉えてください。
n個のマスに候補数字が全n種類ある、ということです。
さて、今度は青色領域と黄色領域には共通の候補数字がありません。
実は、この場合も5マスA〜Eには大きな特徴が潜んでいるんです。
各候補数字の配置に特徴がある。
どんな特徴でしょう?
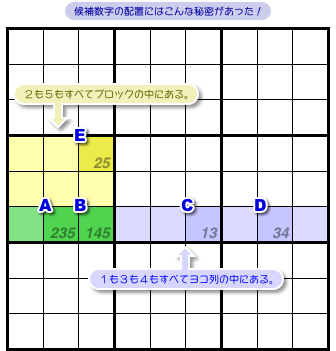
こういう特徴なんです。
- どの候補数字も1列または1ブロックにのみ存在している。
検証してみましょう。
候補数字1はどれも青色ヨコ列に収まっている。
候補数字3, 4も同様。
候補数字2はどれも黄色ブロックに収まっている。
候補数字5も同様。
おぉ、上記の通りだ!
図3-2 の Bent Naked Subset にはこういう特徴があるんです。
果たして、この状況からどういう結論が導かれるんでしょうか?
Bent Naked Subset 自身がとある振る舞いをするようになるんです。
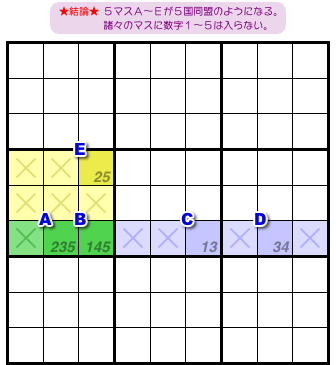
では、結論です。
- マスA〜Eからなる Bent Naked Subset は5国同盟と同じ振る舞いをする。
なんと、5マスA〜Eがまるで5国同盟のようになるという!
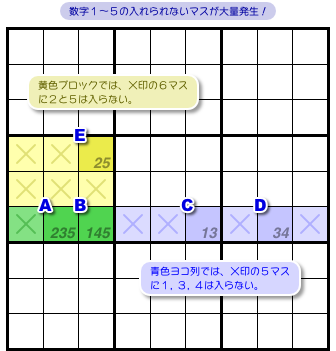
そのおかげで、数字1〜5の入れられないマスが大量発生します。
図3-3 で言うと、青色×印マスに数字1, 3, 4を入れられなくなる。
黄色×印マスに数字2, 5を入れられなくなる。
緑色×印マスに数字1〜5を入れられなくなる。
入れられない数字が山ほど出る!
なぜこういう結論になるのか?
それは、5マスA〜Eに数字1, 2, 3, 4, 5が必ず1個ずつ入ることになるからです。
それを解説しましょう。
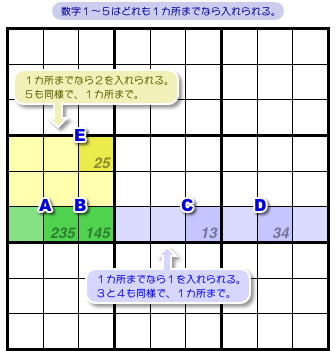
マスA〜Eに数字を入れることを考えてみましょう。
とりあえず、まずはこれが成り立ちます。
- どの候補数字もそれぞれ1個までしか入れられない。
なぜか?
例えば、候補数字1はヨコ1列にしかありません。
マスBかCに数字1を入れられるけれど、どちらかに入れたらもぅ終わり。数字1は最大1カ所にしか入れられません。
また、候補数字2は1ブロックにしかありません。
マスAかEに数字2を入れられるけれど、どちらかに入れたらもぅ終わり。数字2は最大1カ所にしか入れられません。
数字3, 4, 5も同様です。
どれも最大1カ所にしか入れられない。
というわけで、どの数字も1個までなら入れることが可能です。
1個まで、です。
で、ここで1つ疑問が出る。
「1個まで」ということは……もしかして、0個もあり得る?
結論を言うと、それはあり得ません。
なぜか?
例えば、数字1が1個も入らないと仮定しましょう。
すると、数字2〜5だけで5マスを埋め尽くさないといけない。でも、それは不可能なんです。
なぜなら、2〜5も1個までしか入れられないから。
どんなに頑張って数字2〜5で埋め尽くそうとしても、4マスまでしか埋められないのです。
5つめのマスに入れる数字がなく、破綻する😣
というわけで、どの数字も0個はあり得ない。
で、こうなるんです。
- マスA〜Eに数字1, 2, 3, 4, 5は1個ずつ入る。
数字5つが仲良く1部屋ずつ分け合うことになるんですね。
5人のルームシェアだね!
5つの数字が仲良く1個ずつ入る。
これは、こう言い換えられるんです。
- 数字1〜5はどれも必ずマスA〜Eのどこかに入る。
これが判明したのはすごく大きい!
このおかげで、数字1〜5を入れられないマスが生じるんです。
例えば、候補数字1はマスB, Cにありますね。
数字1はB, Cのどちらかに必ず入るのです。
だから、青色ヨコ列において、B, C以外のマスに数字1は入れられなくなった!
図3-6 では、青色&緑色の×印を付けています。
数字3も4も同様で、青色&緑色×印のマスには3も4も入りません。
数字2はA, Eのどちらかに必ず入ります。
だから、黄色ブロックでは、A, E以外のマスに数字2は入りません。
図3-6 では、黄色&緑色の×印を付けています。
数字5も同様で、黄色&緑色×印のマスに5は入りません。
図3-3 の結論通り、まさに5国同盟になりましたね😊
一般的な話をしましょう。
青色領域と黄色領域に共通する候補数字が1つもない場合、次のことが成り立ちます。
- Bent Naked Subset はn国同盟と同じ振る舞いをする。
これが、このセクションにおける一般的な結論です。
Bent Naked Subset とn国同盟は似て非なる物ですが、このセクションの場合は同じ性質を持っていると言って良いでしょう。
n国同盟と同じような理屈で候補数字の大量除去をもたらしてくれるんです。
ただ、残念ながら、このセクションの Bent Naked Subset を使っている場面はあまりありません。
ひとつ挙げるなら、Sue De Coq でしょうか。
私のサイトでは Sue De Coq の一般化のページでも使っています(内容は凄まじく高難度です)。
参考・参照
- Bob Hanson, 『Sudoku Assistant -- Solving Techniques』,
https://www.stolaf.edu/people/hansonr/sudoku/explain.htm#bent
更新履歴
- 2022. 2. 5.
- 新規公開。
- 2023. 3.31.
- ページ冒頭に難易度表記を追加。
- 難易度を4から5へ変更。