1.どういう解法?
Finned X-Wing の舞台は X-Wing と同じ。平行な2列。
その中の4マス+αが繰り広げる解法です。
4マスは X-Wing と同じく矩形状に並んでいるのに、+αのおかげで世界はまったく違います。
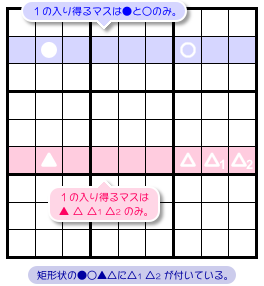
図1-1、青色とピンク色のヨコ2列を見てみましょう。
この2列において数字1の入り得るマスを探したら、次の状況だったとします。
- 青色ヨコ列において、数字1は●と○にしか入らない。
- ピンク色ヨコ列において、数字1は ▲ △ △1 △2 にしか入らない。
- 4マス●○▲△は矩形状に並んでいる。
- △1 △2 は△と同じブロックに属している。
なんだか矩形に尻尾が生えちゃった感じの見た目ですね。
これが Finned X-Wing の最大の特徴です。
これがあるだけで、X-Wing とはまったく異なる結論に至るんです。
ここで、用語をひとつ紹介しましょう。
図1-1 では尻尾のように付いた △1 △2 がありました。これを fin と呼びます。
fin は「ひれ」という意味です。
「ひれの付いた X-Wing」ということで、この解法には Finned X-Wing という名前が付いています。
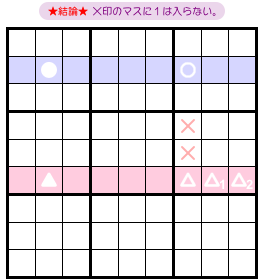
さて、前図1-1 からはどういう結論が得られるんでしょう?
こうなるんです。
- ○ △ △1 △2 の4つすべてと列やブロックを共有するマスがある。そのマスに数字1は入らない。
図1-2 だと×印の2マスが該当します。
この2マスは○と同じタテ列に属しています。同時に、△ △1 △2 と同じブロックに属しています。
この2マスに数字1を入れられなくなるんですね。
なぜ、こういう結論になるんでしょう?
それは、○ △ △1 △2 のうち少なくとも1つに必ず数字1が入るからなんです。
それを解説しましょう。
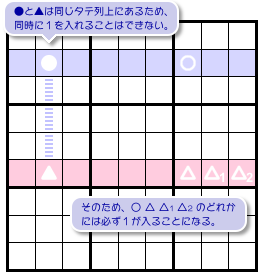
図1-3 の盤面、●と▲が同じタテ列に属していますね。
ということは、●と▲の両方に数字1を入れるということはできません。
つまり、●と▲のうち少なくとも一方には数字1を入れられません。
●に1が入らない場合は、○に必ず1が入ります。
▲に1が入らない場合は、△ △1 △2 のどれかに必ず1が入ります。
ということは、「○に1が入る」「△ △1 △2 のどれかに1が入る」のうち最低1つは成り立つわけですね。
この結果はもっと簡潔に言うことができます。
こんな感じで。
- ○ △ △1 △2 のうち少なくとも1つに必ず数字1が入る。
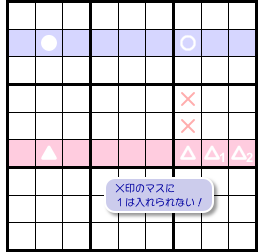
○ △ △1 △2 のうち少なくとも1つに必ず数字1が入る。
そうなると、数字1を入れられないマスが生じます。
×印の2マスです(図1-4)。
その2マスは○とタテ列を共有し、△ △1 △2 とブロックを共有しています。
そして、○ △ △1 △2 のどれかには必ず数字1が入るのだから、×印の2マスには数字1を入れられないわけです。
図1-2 の結論通りになりましたね😊
これが Finned X-Wing です。
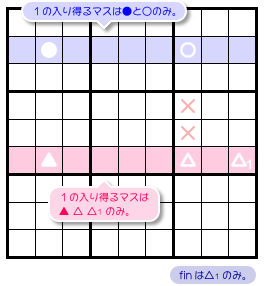
図1-1 では、fin は △1 △2 と2つありました。
実は、fin は1つしかなくてもかまいません(図1-5)。
この場合でも、まったく同じ論理展開ができます。
○ △ △1 のどれかに数字1が入るため、×印のマスに数字1を入れることができないんですね。
ちなみに、fin が1つもない場合はただの X-Wing です。
上記の例では、青色&ピンク色はヨコ列でした。
もちろん、タテ列の場合でも理屈は同じです(fin はタテに並びます)。
その場合については、セクション2で実例を挙げて説明していきましょう。
このページは、単に Finned X-Wing の概要を知りたいという方々へ向けて書いたものです。
Finned X-Wing は Fish 系解法の一種ですが、Fish 系解法において重要な概念が2つあります。
それは ベースセット と カバーセット です。
どの Fish 系解法もその2セットを使って論理展開していくので、Fish 系解法を深く理解したければ2セットの理解は必須です。
この2セットによる Finned X-Wing を知りたい方々は Exofin のページをご覧ください。
2.実際に使ってみよう!
次は、実際の盤面で Finned X-Wing を使ってみましょう。
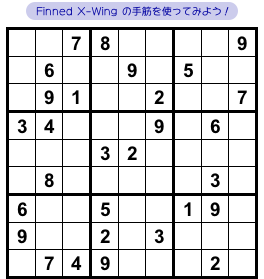
図2-1 では、とあるマスに数字が判明します。
それを Finned X-Wing で突き止めてみます。
ここでは数字5に注目して、5の入り得るマスを探してみます。
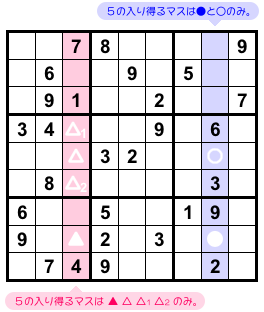
青色とピンク色の2列に注目しましょう(図2-2)。
数字5の入り得るマスは 図2-2 の通りです。
青色の列では●と○の2つ。
ピンク色の列では▲ △ △1 △2 の4つ。
3マス △ △1 △2 は同じブロックにありますね。
そして、●○▲△は矩形状に並んでいます。
fin △1 △2 も付いています!
さぁ、Finned X-Wing の使える形ができました。
使ってみましょう!
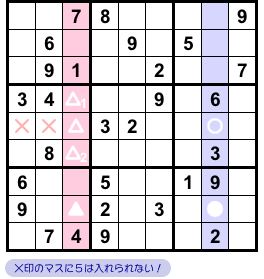
結論はこうです。
- 図2-3、×印の2マスに数字5は入らない。
論理展開を簡単に説明しましょう。
●と▲は同じヨコ列に属していて、両方に数字5を入れるのはNGです。
つまり、●と▲の少なくとも一方には数字5は入りません。
そのため、「○に5が入る」「△ △1 △2 のどれかに5が入る」のうち最低1つは成り立ちます。
これを簡潔に言うとこうなります。
- ○ △ △1 △2 のうち少なくとも1つに必ず数字5が入る。
よって、×印のマスに数字5を入れることはできなくなりました。
うまく Finned X-Wing が使えましたね!
もぅちょっと解き進めてみましょう。
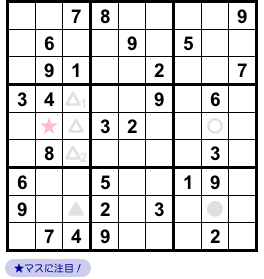
★マス(図2-4)に注目しましょう。
図2-3 での説明により「★マスに数字5を入れられなくなっている」ということに注意してください。
★マスの属する列やブロック全域に目を通すと、★マスには1と5しか入れられないことがわかります。
そして、★マスには数字5が入らないことも既に判明しています。
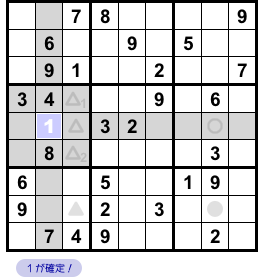
というわけで、★マスに数字1が確定しちゃいました😄
ある列を見て数字Xが2マスにしか入らない時、別の列も見てみましょう。
すると、他の列の状況しだいでは 図1-1 の「矩形状+ひれ」が見えてくるかもしれません。
更新履歴
- 2022. 2. 5.
- 新規公開。
- 2023. 3.31.
- ページ冒頭に難易度表記を追加。