1.Franken Fish って何ぞや?
Swordfish では、次のような状況から論理展開がスタートしました。
ヨコ3列において数字1の入り得るマスを見ると、それらがタテ3列にも並んでいる!
つまり、Swordfish において注目するのはヨコ3列とタテ3列なんですね。
列だけ。
ところが、さらに複雑になった Swordfish もあるんです。
なんと、列の代わりにブロックが交じっている場合がある!
例えばこんな感じ。
ヨコ2列&ブロック1個において数字1の入り得るマスを見ると、それらがタテ3列に並んでいる!
一般に、ノーマルな Fish 系解法はタテn列とヨコn列に注目して論理展開されます。
しかし、列の一部がブロックに置き換わる形でブロックが交じる場合もあるんですね。
交じり方は2種類あります。
- タテ列にのみブロックが交じる。
- ヨコ列にのみブロックが交じる。
この2種類の解法を Franken Fish と呼びます。
Franken Fish は総称で、具体的には Franken Swordfish や Franken Jellyfish などと呼ばれます。
このページでは、Franken Swordfish と Franken Jellyfish の解法を解説していきます。
2.Franken Swordfish
Fish 系の解法を理解するにあたって、基礎となる概念があります。
それは、ベースセットとカバーセットの2つです。
この2つが協力し合って論理展開されていき、候補数字の大量除去が起こります。
このページでは、その2つも説明しながら Franken Fish の解法を解説していきます。
……とその前に、用語を1つ紹介しましょう。
タテ列・ヨコ列・ブロックを全部ひっくるめた総称があります。それを house と言います。
これは英語のナンプレ解説サイトでも使われている用語で、英語の解説を読むと house というワードがやたらと現れます。
以降は house という用語を使うことにしましょう😊
2-1.どういう解法?
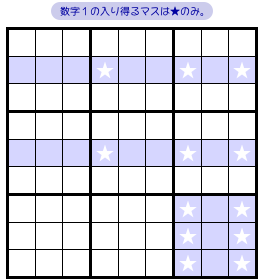
図2-1、3個の青色 house(ヨコ2列&ブロック1個)を見てみましょう。
それぞれ数字1の入り得るマスを探したら、★の12カ所しかなかったとします。
これらの★マスはすべて青色 house 内部に存在していますね。
もちろん、それは当たり前😊
しかし、この12個のマスにはもうひとつ特徴があるんです。
どんな特徴でしょう?
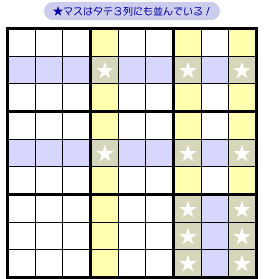
実は、12個の★マスはタテ3列にも並んでいるんです。
図2-2、黄色タテ3列です。
というわけで、前図2-1 からはこういう状況になりました。
- 3個の青色 house において、数字1は★マスにしか入らない。
- そして、その★マスすべてを黄色タテ3列で覆い尽くせた!
元々、12個の★マスはすべて青色 house に属しています。
しかし、それと同時に黄色タテ列にも属している、というわけです。
青色と黄色、2つのセットが出てきましたね。
この2つがキーとなって、論理展開が繰り広げられていくことになります。
ここで、ベースセットとカバーセットの説明をしましょう。
図2-2 の状況になった時、最初の青色 house を全部まとめて ベースセット と呼びます。
そして、★マスを覆い尽くした黄色3列を全部まとめて カバーセット と呼びます。
図2-2 ではベースセットもカバーセットも3個の house で構成されていますが、実は、これはすごく重要です。
ベースセットとカバーセット、両者の house の個数は必ず同じでなければいけません。
一方が3個なら他方も3個です。
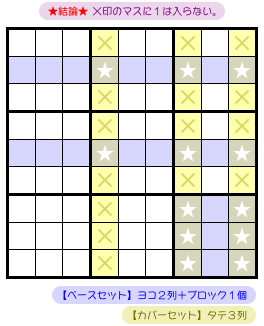
さて、前図2-2 からはどういう結論が得られるんでしょう?
こうなるんです。
- カバーセットにおいて、★以外のマスに数字1は入らない。
つまり、★以外のすべての黄色マスに数字1は入らない。
図2-3 だと×印のマスが該当します。
うゎ〜、バツばっかり! ★以外の黄色マス、全滅!
カバーセットに多大な影響を及ぼすんですね。
なんと、バツは総勢15マス!
なぜ、こういう結論になるんでしょう?
それを解説しましょう。
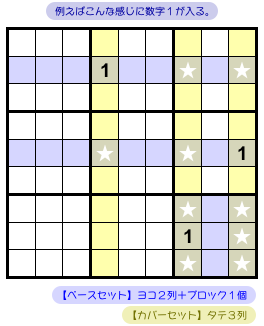
今、カバーセット(黄色タテ列)を一旦忘れて、3個の青色 house に試しに数字1を1個ずつ入れてみることにします。
さて、数字1の入れ方は何通りあるでしょう?
答えは12通りです。
全パターンをこのページに挙げてみました。図2-4 はその一例です。
実は、この12通りには大きな共通点があるんです。
それは……
- どの黄色タテ列を見ても、数字1は必ず★マスに入っている。
なんと!
★以外の黄色マスに数字1が入っていないのです。
青色 house に数字1を入れていっただけなのに、どうしても黄色列はこの状態になってしまいます。
そのため、黄色タテ列において★以外のマスに1が入る可能性はないんですね。
図2-3 の結論通りになりましたね😄
これが Franken Swordfish です。

上記の例では12個の★が整列していました。
しかし、本当は★の整列が多少欠けていてもかまいません(図2-5)。
★が少なくても、図2-4 と同じ論理展開ができます。
大事なのは、ベースセット内部にあるすべての★マスがカバーセット内部にも存在するということです。
それさえ満たしていれば、★の個数は関係ありません。
上記の例ではベースセットの方にブロックが交じっていましたが、カバーセットの方に交じっている場合もあります。
その場合も理屈は同じです。
セクション2-2で実例を挙げて説明していきましょう。
2-2.実際に使ってみよう!
次は、実際の盤面で Franken Swordfish を使ってみましょう。

図2-6 では、とあるマスに数字が判明します。
それを Franken Swordfish で突き止めてみます。
ここでは数字2に注目して、2の入り得るマスを探してみます。
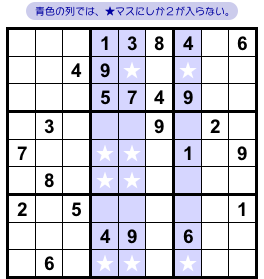
青色のタテ3列に注目しましょう!(図2-7)
各列において★にしか数字2は入りません。
★は9つありますね。
さて、この9つの★マスをすべて覆い尽くせる3個の house はあるでしょうか……?
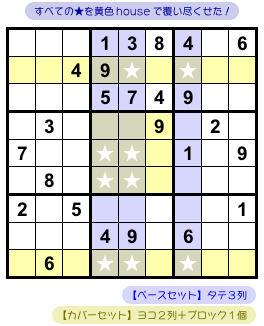
ありました!
図2-8、黄色のヨコ2列&ブロック1個、合計3個の house が9個の★マスをすべて含んでいますね。
というわけで、前図2-7 からはこういう状況になりました。
- 青色タテ3列において、数字2の入り得るマスは★だけだった。
- そして、その★マスすべてを3個の黄色 house で覆い尽くせた!
ベースセットは青色タテ3列です。
カバーセットは黄色ヨコ2列&ブロック1個です。
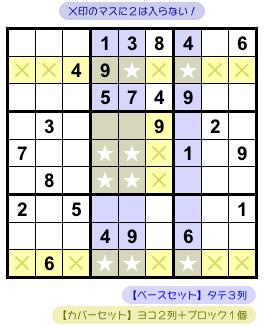
さぁ、カバーセットが見つかりました。
セクション2-1で説明した結論を適用してみましょう。
- カバーセットにおいて、★以外のマスに数字2は入らない。
つまり、★以外のすべての黄色マスに数字2は入らない。
図2-9 だと×印のマスに数字2は入りません。
うゎ~、ものの見事にバツだらけ!
凄まじく数字2が入らなくなった!
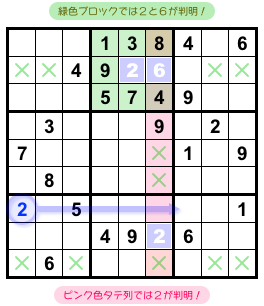
うまく Franken Swordfish が使えましたね!
もぅちょっと解き進めてみましょう。
これだけバツが大量発生したら、あとは数字がいろいろ判明します。
緑色ブロックでは2の入り得るマスは1つしかないし、6も判明します。
ピンク色タテ列でも2の入り得るマスは1つだけ。
なんと、3カ所も判明しましたね😄
3.Franken Jellyfish
次は、Franken Jellyfish を解説していきましょう!
本質的には Franken Swordfish と変わりないので、理解はそれほど難しくはありません。
3-1.どういう解法?
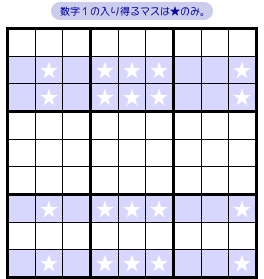
図3-1、青色のヨコ4列を見てみましょう。
それぞれ数字1の入り得るマスを探したら、★の20カ所しかなかったとします。
これらの★マスがすべて青色ヨコ列に存在するのはもちろん当たり前😊
実は、この20個の★マスにはもうひとつ特徴があるんです。
どんな特徴でしょう?
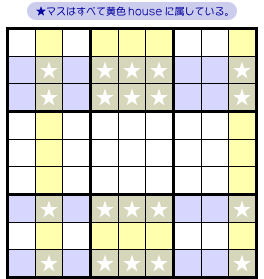
実は、4個の house(タテ2列&ブロック2個)が20個の★マスをすべて含んでいるんです。
というわけで、前図3-1 からはこういう状況になりました。
- 青色ヨコ4列において、数字1は★マスにしか入らない。
- そして、その★マスすべてを4個の黄色 house で覆い尽くせた!
元々、20個の★マスはすべて青色ヨコ列に属しています。
しかし、それと同時に黄色 house にも属している、というわけです。
青色と黄色、2つのセットが出てきましたね。
この2つがキーとなって、論理展開が繰り広げられていくことになります。
ここで、ベースセットとカバーセットの説明をしましょう。
図3-2 の状況になった時、最初の青色4列を全部まとめて ベースセット と呼びます。
そして、★マスを覆い尽くした黄色 house を全部まとめて カバーセット と呼びます。
図3-2 ではベースセットもカバーセットも4個の house で構成されていますが、実は、これはすごく重要です。
ベースセットとカバーセット、両者の house の個数は必ず同じでなければいけません。
一方が4個なら他方も4個です。

さて、前図3-2 からはどういう結論が得られるんでしょう?
こうなるんです。
- カバーセットにおいて、★以外のマスに数字1は入らない。
つまり、★以外のすべての黄色マスに数字1は入らない。
図3-3 だと×印のマスが該当します。
凄まじくバツバツしい! ★以外の黄色マス、全滅!
こんなにも数字1が入らなくなるんですね。
なぜ、こういう結論になるんでしょう?
それを解説しましょう。
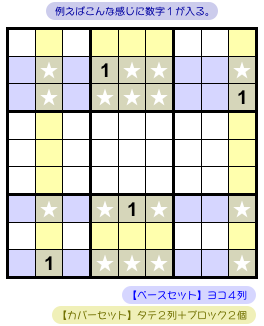
今、カバーセット(黄色 house)を一旦忘れて、4個の青色ヨコ列に試しに数字1を1個ずつ入れてみることにします。
さて、数字1の入れ方は何通りあるでしょう?
答えは48通りです。
全パターンを……って、さすがに48通りも挙げるのはシンドイ😅
実は、全パターンを挙げずに次が正しいことは証明できます。
- どの黄色 house も数字1は★の位置にしか入らない。
といっても、話は長くなっちゃうもんで、このページで示しました。
ヒマでしょうがない時にでも読んでやってください😄
ま、とにかく、黄色 house において★マスにしか数字1は入りません。
★以外のマスは可能性ゼロなんです。
図3-3 の結論通りになりましたね😄
これが Franken Jellyfish です。
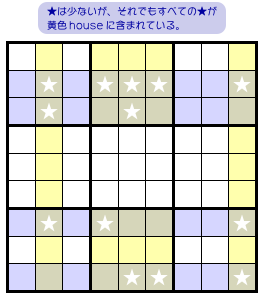
上記の例では20個の★が整列していました。
しかし、本当は★の整列が多少欠けていてもかまいません(図3-5)。
★が少なくても、前図3-4 と同じ論理展開ができます。
大事なのは、ベースセット内部にあるすべての★がカバーセット内部にも存在するということです。
それさえ満たしていれば、★の個数は関係ありません。
上記の例ではカバーセットの方にブロックが交じっていましたが、ベースセットの方に交じっている場合もあります。
その場合も理屈は同じです。
セクション3-2で実例を挙げて説明していきましょう。
3-2.実際に使ってみよう!
次は、実際の盤面で Franken Jellyfish を使ってみましょう。

図3-6 では、とあるマスに数字が判明します。
それを Franken Jellyfish で突き止めてみます。
ここでは数字9に注目して、9の入り得るマスを探してみます。
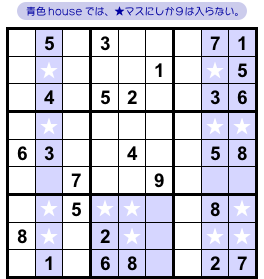
青色のタテ3列とブロック1個に注目しましょう!(図3-7)
それぞれ★マスにしか9は入りません。
さて、これらの★マスをすべて覆い尽くせるヨコ4列はあるでしょうか……?
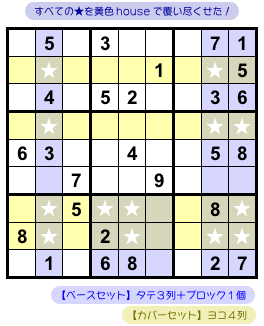
ありました!
図3-8、黄色のヨコ4列が★マスをすべて含んでいますね。
というわけで、前図3-7 からはこういう状況になりました。
- 4個の青色 house において、数字9の入り得るマスは★だけだった。
- そして、その★マスすべてを黄色ヨコ4列で覆い尽くせた!
ベースセットは青色タテ3列&ブロック1個です。
カバーセットは黄色ヨコ4列です。
さぁ、カバーセットが見つかりました。
セクション3-1で説明した結論を適用してみましょう。
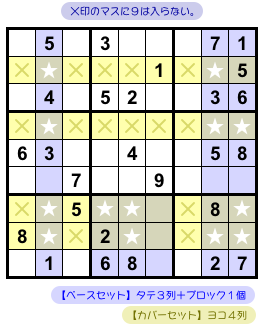
- カバーセットにおいて、★以外のマスに数字9は入らない。
つまり、★以外のすべての黄色マスに数字9は入らない。
図3-9 だと×印のマスに数字9は入りません。
うゎ~、これもまた凄まじくバツだらけ!
9の入れられないマスが山ほど現れた!
うまく Franken Jellyfish が使えましたね!
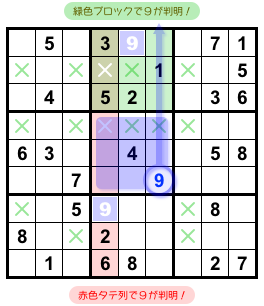
もぅちょっと解き進めてみましょう。
大量発生したバツのおかげで、2マスに数字が判明します。
緑色ブロックと赤色タテ列、どちらも数字9の入り得るマスは1つしかありません。
更新履歴
- 2022. 2. 5.
- 新規公開。
- 2023. 3.31.
- ページ冒頭に難易度表記を追加。