1.どういう解法?
Swordfish の舞台は平行な4列。
その中に住む最大16マスが繰り広げる世界です。
それらのマス達はタテヨコに綺麗に整列し、その位置関係が強烈なまでに効力を発揮する!
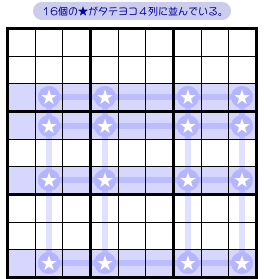
図1-1、青色ヨコ4列を見てみましょう。
この4列において数字1の入り得るマスを探したら、次の状況だったとします。
- それぞれの青色ヨコ列において、数字1は★マスにしか入らない。
- 4つの★マスがタテにも並んでいる。
★がヨコに4つずつ並んでいるのは当たり前😊
でも、タテにも4つずつ並んでいる。
まさに網目のようにキッチリ整列しているんですね。
綺麗な整列です🥰
この位置関係が後々大きな影響を及ぼしていくんです。
★マスの並んだタテ4列、そこに大きな変化が現れます!
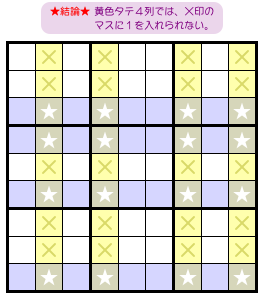
さて、図1-1 からはどういう結論が得られるんでしょう?
こうなるんです。
- 黄色のタテ列において、★以外のマスに数字1は入らない。
図1-2 だと、×印のマスが該当します。
このマスに数字1を入れられなくなるんです。
数えてみたら、なんと20マス!
おびただしい数のマスに数字1が入らなくなるんですね。
なぜ、こういう結論になるんでしょう?
それを解説しましょう。
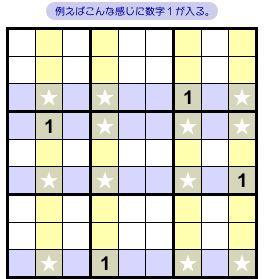
今、黄色タテ列を一旦忘れて、青色ヨコ列に試しに数字1を1個ずつ入れてみることにします。
さて、数字1の入れ方は何通りあるんだろう?
答えは 20通りです。
全パターンをこのページに挙げてみました。図1-3 はその一例です。
実は、この 20通りには共通点があるんです。
- どの黄色タテ列を見ても、数字1は★の位置にしか入っていない。
20パターンを全部見ればわかりますが、ものの見事に★マスにしか数字1が入っていない!
★以外の黄色マスに数字1が入る可能性はゼロなんですね。
図1-2 の結論通りになりましたね😄
これが Jellyfish です。
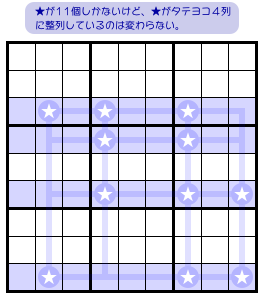
上記の例では、16個の★がタテヨコ4列に整列していました。
しかし、本当は★がキッチリ16個並んでいる必要はありません。
例えば 図1-4 のような感じ。
実は、★が少なくても 前図1-3 と同じ論理展開ができます。
大事なのは、★がタテにもヨコにも整列しているということです。
それさえ満たしていれば、★の個数は関係ありません。
上記の例では、青色はヨコ列、黄色はタテ列でした。
もちろん、タテヨコ逆でも理屈は同じです。
タテヨコ逆の場合は、セクション2で実例を挙げて説明していきましょう。
このページは、単に Jellyfish の概要を知りたいという方々へ向けて書いたものです。
Jellyfish は Fish 系解法の一種ですが、Fish 系を深く理解するためには2つの概念を必ず知らなければいけません。
それは ベースセット と カバーセット です。
どの Fish 系解法もベースセットとカバーセットを使って論理展開していくので、この2セットを使いこなせれば Fish 系はもぅ完璧にわかります。
この2セットによる Jellyfish を知りたい方々は ベースセットとカバーセット のページをご覧ください。
2.実際に使ってみよう!
では、実際の盤面で Jellyfish を使ってみましょう!
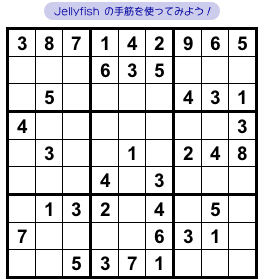
図2-1 では、とあるマスに数字が判明します。
それを Jellyfish で突き止めてみます。
ここでは数字6に注目して、6の入り得るマスを探してみます。
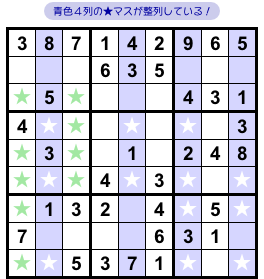
図2-2、数字6の入り得るマスを★と▲で表しました。
ここで、青色のタテ4列に注目しましょう。
その4列の★を見てみると……なんと、12個の★がタテヨコに整列している!
これはまさに Jellyfish の使える形ですね。
使ってみましょう!
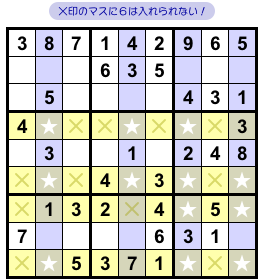
前セクションで示した結論を適用してみましょう。
こうなります。
- 黄色ヨコ列において、★以外のマスに数字6は入れられない。
図2-3、×印のマスに数字6を入れることができなくなりました。
もぅもぅもぅバツだらけです。
大量10マスものシャットアウト! 数字6を入れられなくなりました。
これが Jellyfish の力です。
うまく Jellyfish が使えましたね!
もぅちょっと解き進めてみましょう。
前図2-3 では数字6の入らないマスが大量発生しました。
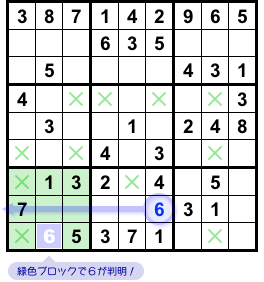
その上で、今度は緑色ブロックに注目します。
なんと、バツのおかげで、6の入るマスはたった1つだけ(図2-4)。
数字6が確定しちゃいました😄
図2-3 で大量に×印がついたように、Jellyfish は非常に効果的な解法です。
ところが、Jellyfish は本当に本当に見つけづらい! 凄まじく見つからない!
でも、Jellyfish は4列も使う大がかりな解法だから、一生に一度は豪快にキメてみたいもんです😄
3.Fish とn国同盟の意外な関係
ここからは余談です。
X-Wing や Swordfish などの Fish 系解法は、実はかなり効率的です。多くのマスに作用しますもんね。
しかし、一般には盤面から Fish を見つけるのは困難です。
見つけやすいのはせいぜい Swordfish までで、まぁ〜盤面に目を凝らしてもホントに見つからん!
ところが。
Fish を見つけやすくする方法があるというのです!
しかも、その方法を使うと、Fish をまるでn国同盟のように扱えるという!
このセクションでは、その話をしようと思います。
この話は、『The New Sudoku Players' Forum』の a new (?) view of fish (naked or hidden) というトピックで見られます。
それを基に解説していきます。
これは Jellyfish に限った話ではないですが、このページで紹介します。
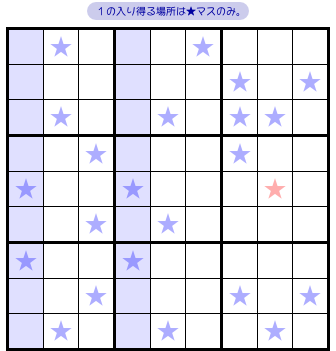
図3-1、部分図です。
今、数字1は★マスにしか入らないとしましょう。
この図には X-Wing が隠れています。
青色のタテ2列ですね。
そして、その X-Wing により「赤色★マスに数字1が入らなくなる」という結論が得られます。
これを頭の片隅に置いといてください。
さて。
ここで、あることを行います。
各タテ列に対して、こういうことを考えてみましょう。
上から何マス目に★が存在しているか?
★の位置を各タテ列ごとにメモしていくわけです。
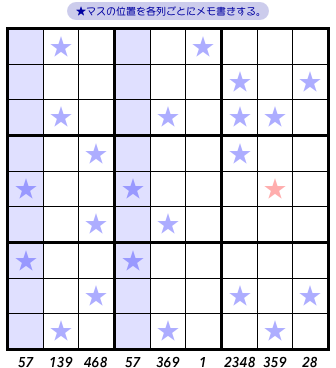
各タテ列ごとに★の位置をメモしました。
図3-2、盤面の下に記しておきます。
- 57 139 468 57 369 1 2348 359 28
このメモを見てみると、あることに気付きます。
青色2列に対応する数字、両方とも同じですね。
57 です。
そして、赤色★のあるタテ列には 359 があります。
X-Wing によって赤色★マスに数字1が入らなくなるわけなので、この 359 からは 5 が除去されることになるでしょう。
2個の 57 があり、359 から 5 が消える。
……あれ?
これって、なんか2国同盟っぽいような……?
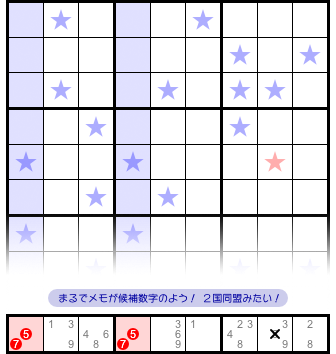
そうなんです。
メモ数字を候補数字だとみなすと、まさに2国同盟(Naked Pair)と同じ挙動が現れるんです。
X-Wing による結果、疑似2国同盟による結果、両者はちょうど1対1に対応しているんですね。そのため、両者の結果は本質的に同じだと言えます。
というわけで、Fish を疑似n国同盟の視点で考察することが可能なんですね。
数字kの Fish を見つけたい時は、次のことを行えば良い。
こういうことになりますね。
- 候補数字kのマス位置をメモ書きし、そのメモからn国同盟を探す。それを行えば数字kの Fish が盤面に存在するか否かを知ることができる。そして、そのメモ数字にn国同盟を適用すれば、Fish による結果を知ることができる。
これが Fish とn国同盟の意外な関係です。
いやぁ~、思いもよらないところで両者はつながっていたんですねぇ~😊
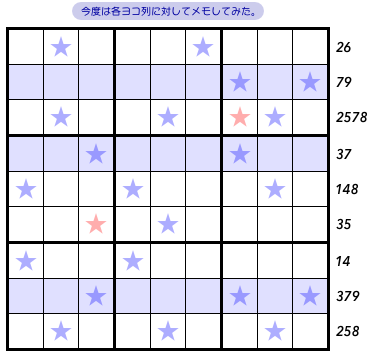
今度は、各ヨコ列に対して「左から何マス目に★が存在するか?」ということを考えてみましょう。
図3-4 には Swordfish も隠れています。
青色のヨコ3列です。
この Swordfish によって赤色★マスに数字1を入れられなくなりますね。
これを頭に入れておきましょう。
さて、メモするとこうなりました。
- 26 79 2578 37 148 35 14 379 258
青色3列のメモは 79, 37, 379 ですね。
もぅもぅ、見るからに3国同盟の匂いがプンプンです😃
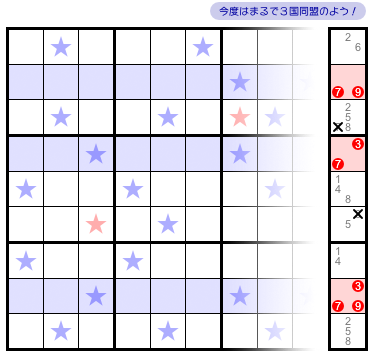
もちろん、その匂いプンプンの通りです。
メモ数字を候補数字だとみなすと、3国同盟(Naked Triple)と同じ挙動が現れるんです。
疑似3国同盟によって 7 と 3 が除去される形になりますが、これは「赤色★マスに数字1が入らなくなる」と同じ意味を持っています。
この場合も Fish を疑似n国同盟に置き換えて考察できるんですね。
ちなみに、このメモ書きの中には数字1, 4の2国同盟(Hidden Pair)も隠れています。
確認してみてください。
図3-1 の X-Wing と併せて確認すると、何かに気付くかもしれない……?
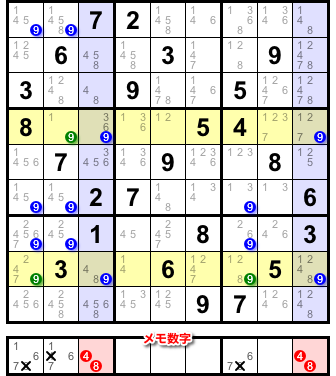
具体例を1つ。
X-Wing のページで紹介した盤面です。
青色のタテ2列では数字9の X-Wing が発生していて、その影響で黄色マスの候補数字9が除去されようとしているところです。
各タテ列に対して候補数字9のある場所をメモしましょう。
すると、メモ内部で疑似2国同盟が発生していますね。
メモ数字 4 と 8 が除去される形になるわけですが、それは盤面の9にちょうど対応しているんですね。
この変換作業、視認性は良くなるけれど、人力では大変かもしれません。
数字1に対してメモ書き、数字2に対してメモ書き、……、これを繰り返すから作業量は結構多い。
ただ、プログラミングの視点で考えると、案外有用な方法かもしれない?
もし効率的なn国同盟処理が既にできていれば、Fish をn国同盟に変換して処理できる。
この考えを実際に採用しているソフトがあるかどうかは知りませんが、Fish 系解法の処理としては役に立つかもしれない。
そんなことをふと思いつきました。
あ、これは素人考えなんで話半分に聞いてください😅
ちなみに、この変換作業はノーマルな Fish にしか通用しません。
Franken Fish, Mutant Fish, Finned Fish などの特殊な Fish には使えません。
そう考えると、この変換処理にはそれほど汎用性はない。
役には立たんかもなぁ😓
参考・参照
- The New Sudoku Players' Forum, 『a new (?) view of fish (naked or hidden)』,
http://forum.enjoysudoku.com/a-new-view-of-fish-naked-or-hidden-t5017.html
更新履歴
- 2022. 2. 5.
- 新規公開。
- 2023. 3.31.
- ページ冒頭に難易度表記を追加。