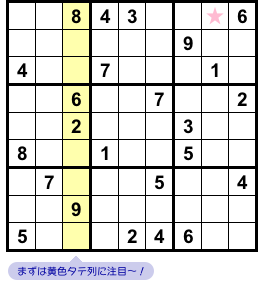
2.見えないけれど、座布団レーザーで候補を減らせる!
前セクションでは、ステルス座布団レーザーと他のレーザーを組み合わせて解き進めました。
実は、ステルス座布団レーザーにはもうひとつの効果があるんです。
「マスに入り得る数字を1つ減らす」という効果です。
図2-1 の★マスには数字が判明します。
と言っても、これもパッと見ではまったくわかりません。
とりあえず、今は★マスはおいといて、黄色ヨコ列に注目しましょう。
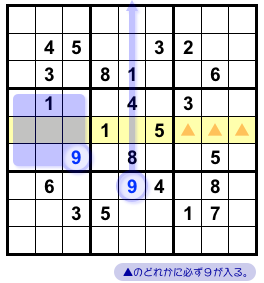
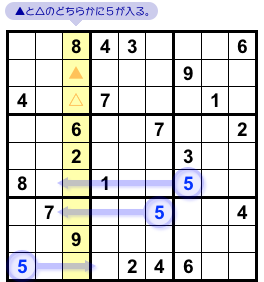
数字9から黄色ヨコ列へレーザーを発射してみましょう。
左側のは座布団レーザーです。
黄色ヨコ列では、3カ所の▲のどれかに9が入ることになりました。
もちろん、どの▲に9が入るのかはまだわかりません。
ただ、3つの▲についてこんなことが言えますね。
- どの▲も同じブロックに属している。
▲はすべて同じブロック内部にある。
ここがミソなんです。
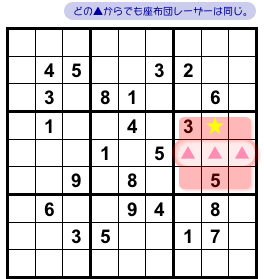
どの▲も同じブロック内部にある。
ということは、その3マスから発射する座布団レーザーはどれも同じです。
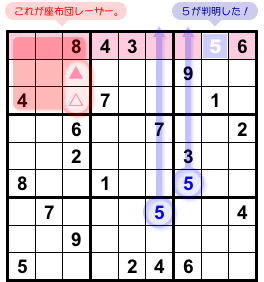
図2-3、赤色の四角です。
現時点では、どの▲に数字9が入るかはわかりません。
しかし、どこに入ろうとも座布団レーザーは必ず発射できる。
というわけで、これが成り立つことになるんです。
- 赤色レーザーの通ったマスに数字9は入らない。
このことが★マスに影響を及ぼしていくんです。
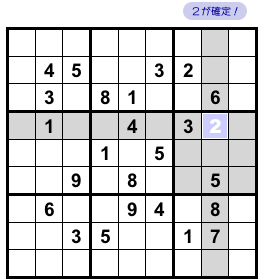
その★マスの属する列やブロック全域に目を向けてみましょう。
その中には2と9以外の数字が既に存在します。
ということは、★マスには2か9のどちらかしか入らないんですね。
……と、ここで、さっきの座布団レーザーが効いてくる!
★マスに数字9は入らないと判明したばかりでしたね。
つまり、2以外はすべてダメになったのです。
というわけで、★マスに数字2が確定です!
もともと、★マスに入り得る数字は2と9でした。
しかし、「見えない座布団レーザー」によって数字9の可能性が消えた。
こういうふうに、密かに数字の可能性を1つ消してくれる。
ステルスレーザーにはそういう力があるんですね。
ただ、コッソリと消すので、なかなか気付けない😓
数字9の場所は見えていない。
けれど、数字9から発射する座布団レーザーはわかる。
その「見えないレーザー」が×印マスに直撃して、数字確定につながったわけなんですね。
3.候補数字という視点で見てみよう!
ここからは余談です。
セクション1では、ステルス座布団レーザーを発射して数字5の場所を突き止めました。
このセクションでは、「intersection」という概念を用いて候補数字の視点からもう少し詳しく解説していきます。
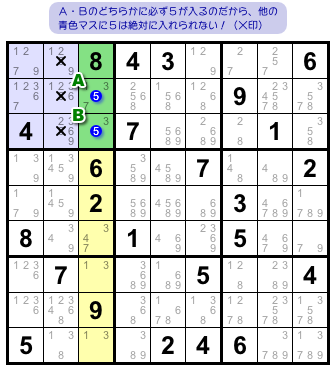
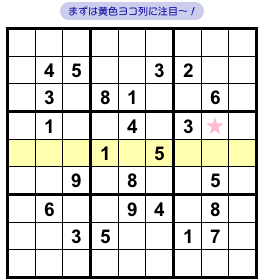
図1-1 の盤面、各マスに入り得る数字を列挙してみると、図3-1 のようになりました。
この薄くて小さい数字をそのマスの 候補数字 と呼びます。
図3-1 の黄色タテ列に注目してみると、候補数字5を持つマスはA, Bの2つだけですね。
だから、次のことがわかります。
- 2マスA, Bのどちらかに必ず数字5が入る。
これを踏まえながら青色ブロックを見てみましょう。
すると……、
A, B以外の青色マスに5は入れられない!
だって、AかBに必ず5が入るんだもん!
青色ブロックの立場からすると、数字5の入る可能性は既に2マスA, Bに絞られちゃっていたんですね。黄色タテ列のおかげで。
だから、A, B以外の青色マスから候補数字5を除去できる。
図3-1 はそういう盤面でした。
ここで、ナンプレの用語をひとつ紹介しましょう。
図3-1 では黄色列と青色ブロックが交わっていますね。交差箇所を緑色で表しています。
この緑色領域のことを intersection と呼びます。
ちなみに、英単語 intersection は「交差」という意味です。まんま。
実は、このページの解法は intersection を利用した物なんです。
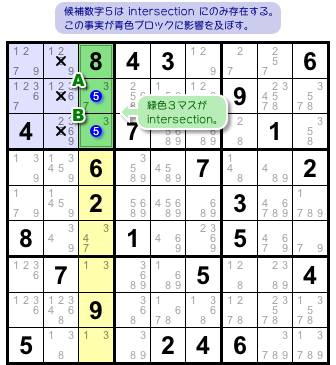
2マスA, Bには共通点があります。
- AもBも同じ intersection に属している。
確かに、A, B両方とも緑色 intersection に存在してますね。
このことが青色ブロックに影響を及ぼすわけなんです。
あらためて、前図3-1 の論法を説明しましょう。
黄色タテ列を見ると、候補数字5は intersection 内部にしか存在していない。
すると、その intersection 領域をまるごと含む青色ブロックでは、数字5の入る場所が intersection 内部に制限された状態になっている。
よって、intersection の外にある青色マスから候補数字5を除去できました。
青色ブロックの視点で見ると、黄色タテ列によって候補数字5がロックされちゃったように見えますね。
「5は緑色から外に出るなよ〜!」と先手を打たれたかのよう。
この解法は海外では Locked Candidates と呼ばれています。
まさに「ロックされた候補数字」なんですね。
この Locked Candidates、実は2種類あります。
ひとつは、このページで解説した通り、以下の手順で論理展開していきます。
- 列をちょっと調べてみよう!
- あら、候補数字nは intersection にしか存在しなかったよ!
- じゃぁ、その intersection をまるごと含むブロックでは候補数字nをボロボロ除去できるね!
視点が 列・intersection・ブロック と順に移り変わってますね。
この解法には「Claiming」というサブネームが付いていて、Locked Candidates (Claiming) と呼ばれています。
もうひとつは、上記とは逆方向です。
視点が ブロック・intersection・列 と順に移り変わっていきます。
これには「Pointing」というサブネームが付いていて、Locked Candidates (Pointing) と呼ばれています。
その解法は『ステルスレーザー発射!』のページで紹介しています。併せてご覧ください。
更新履歴
- 2022. 2. 5.
- 新規公開。
- 2023. 3.31.
- ページ冒頭に難易度表記を追加。