【解法】XYZ-Wing

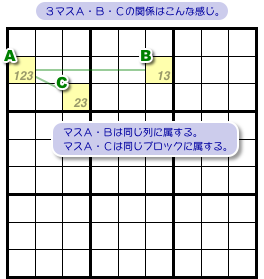
　今、３マスＡ, Ｂ, Ｃについて、次の状況になっているとしましょう。

• マスＡには数字１, ２, ３のみが入り得る。
• マスＢには数字１と３のみが入り得る。
• マスＣには数字２と３のみが入り得る。
• マスＡとＢは同じ列に属している（ただしブロックは異なる）。
• マスＡとＣは同じブロックに属している（同じ列に属しても良い）。
• マスＡ, Ｂ, Ｃは一直線上にない。

　んも〜、条件多すぎる😅
　図1-1 を見てビジュアル的に理解しちゃってください😅

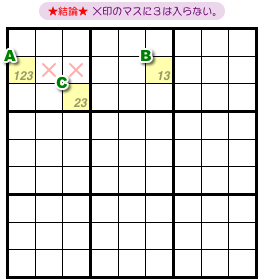
　さて、前図1-1 からはどういう結論が得られるんでしょう？
　こうなるんです。

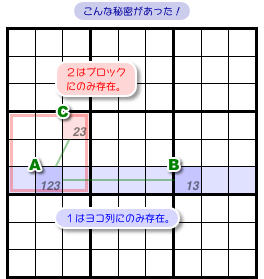
• ３マスＡ〜Ｃすべてと列やブロックを共有するマスがある。そのマスに数字３は入らない。

　図1-2 だと×印の２マスが該当します。
　その２マスはマスＡ, Ｂとヨコ列を共有し、マスＣとブロックを共有しています。
　その２マスに数字３は入らないというわけです。

　なぜこういう結論になるんでしょう？
　それは、３マスＡ〜Ｃのどこかに必ず数字３が入るからなんです。
　それを解説しましょう。

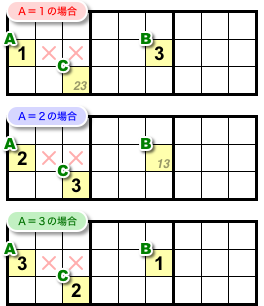
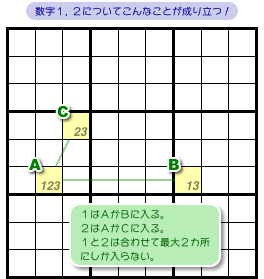
　マスＡの候補は３つあります。
　そして、Ａに入った数字によってマスＢ, Ｃに影響が出ます。

　マスＡに１が入った場合、マスＢに必ず３が入ります。
　マスＡに２が入った場合、マスＣに必ず３が入ります。
　マスＡに３が入った場合、ＢもＣも数字が確定します。

　図1-3 の３パターンを見て、どういうことが言えるんでしょう？
　数字３について、何かが見えてきそう……。
　実は、こういうことが言えるんです。

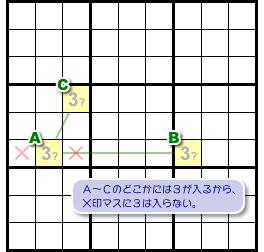
• マスＡ, Ｂ, Ｃのどこかに必ず数字３が入る。

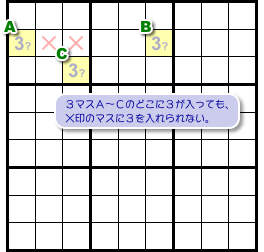
　そうなると、数字３を入れられないマスが生じます。
　図1-4、×印のマスです。

　×マスは２マスＡ, Ｂとヨコ列を共有し、マスＣとブロックを共有しています。
　だから、Ａ, Ｂ, Ｃのどこに数字３が入ったとしても、×マスには３を入れることができないんです。

　図1-2 の結論通りになりましたね😊
　これが XYZ-Wing の解法です。

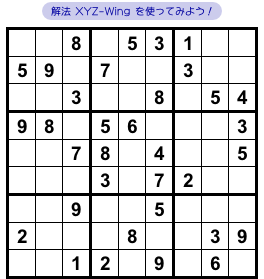
　図2-1 では、とあるマスに数字が判明します。
　それを XYZ-Wing で突き止めてみます。

　各マスの入り得る数字を調べてみましょう。

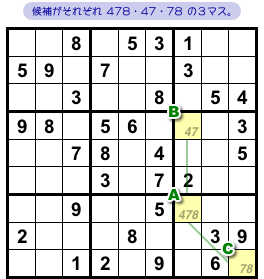
　図2-2、Ａ〜Ｃの３マスに注目します。
　さて、状況はどうなっているでしょう？

• マスＡには数字４, ７, ８のみが入り得る。
• マスＢには数字４と７のみが入り得る。
• マスＣには数字７と８のみが入り得る。
• マスＡとＢは同じ列に属している（ただしブロックは異なる）。
• マスＡとＣは同じブロックに属している。
• マスＡ, Ｂ, Ｃは一直線上にない。

　これは XYZ-Wing が使えますね！
　早速使いましょう！

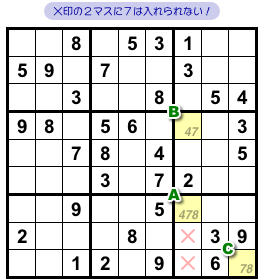
　結論はこうなります。

• 図2-3、×印のマスに数字７は入らない。

　マスＡには４, ７, ８のどれかが必ず入ります。
　すると、入った数字に応じてマスＢ, Ｃに影響が出ます。

　マスＡに４が入った場合は、マスＢに必ず７が入ります。
　マスＡに７が入った場合は、マスＢもＣも数字が確定します。
　マスＡに８が入った場合は、マスＣに必ず７が入ります。
　結局、３マスＡ, Ｂ, Ｃのどこかに数字７が入ることになるんですね。

　というわけで、×印のマスに数字７を入れることができなくなりました（図2-3）。

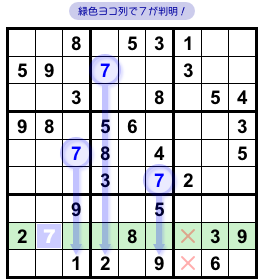
　うまく XYZ-Wing が使えましたね！
　もぅちょっと解き進めてみましょう。

　緑色ヨコ列（図2-4）に注目しましょう。
　×印マスに数字７が入らないことも踏まえると……

　なんと、緑色ヨコ列で数字７が判明しちゃいました😊

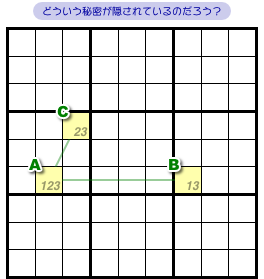
　図3-1 の盤面、３マスＡ〜Ｃで XYZ-Wing の形ができています。
　この３マスで解説していきましょう。

　まず、パッと見でわかる特徴は、候補数字が全３種類だということ。
　３マスで全３種類。
　まるで３国同盟みたいですね。
　ただ、残念ながらこれは３国同盟ではありません。

　それとは別に、もうひとつ特徴があるんです。
　各候補数字の配置、これに大きな特徴が潜んでいる。
　どんな特徴なんでしょう？

　実は、候補数字の配置がそれぞれこうなっているんです。

• 候補数字１はただ１つの列に存在している。
• 候補数字２はただ１つのブロックに存在している。
• しかし、候補数字３は複数の列やブロックに存在している。

　たしかに、図3-2 を見ると一目瞭然だ！
　１はどれも青色ヨコ列に収まっている。
　２はどれも赤色枠のブロックに収まっている。
　３は列＆ブロック両方にまたがっている。
　まさに上記の特徴通り。

ただ１つの候補数字を除いて、どの候補数字もただ１つの列またはブロックに収まっている。

　これが、XYZ-Wing の持つ大きな特徴なんです。

　実は、３マスＡ〜Ｃに対して成り立つことが１つあるんです。

• 数字１も２も１個までしか入れられない。
  つまり、数字１, ２は合計２個までしか入れられない。

　なぜでしょう？
　例えば、候補数字１はヨコ１列にしかありません。
　マスＡかＢに数字１を入れられるけれど、１カ所に入れたらもぅ終わり。他のマスには１を入れられない。
　数字２も同様で、最大１カ所にしか入れられません。

　３マスＡ〜Ｃのうち２マスまでなら数字１と２で埋められる。
　逆に言えば、数字１, ２だけでは最大２マスまでしか埋まらないんです。
　あれ？　マスはまだ残ってるよ？
　残りは……どうするの？

　そうです。数字３で埋めるしかないんです。
　だって、数字１と２で埋めきれないんですもの！　３も使うしかない！

　数字１, ２だけでは３マスを埋め尽くせない。
　どうしても数字３が必要になる。
　というわけで、３マスＡ〜Ｃについてこういう結果に至るんです。

• ３マスＡ〜Ｃのどこかに必ず数字３を入れなければならない。

　実際は、候補数字３はＡ〜Ｃすべてにあります。
　だから、そのどれかには必ず数字３が入ることになりますね。

　この結果を経て「×印マスに数字３は入らない」という結論に至ります。
　セクション１とは論法が異なりますが、同様の結論になりました。

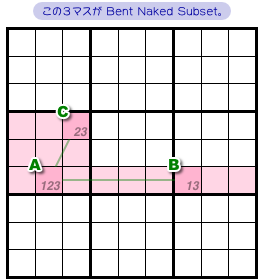
　ここで、３マスＡ〜Ｃの配置について話をひとつ。
　実は、名前が付いています。

　この３マスはピンク色領域に存在していますね。
　１列と１ブロックを合成したＬ字型の領域です。
　簡単に言うと、マスＡ〜Ｃは「折れ曲がった形」に配置されているわけです。

　この３マスＡ〜Ｃをひっくるめて Bent Naked Subset と呼びます。
　bent は「曲がっている」という意味。
　Naked Subset とはｎ国同盟という意味。
　３マスだと Bent Naked Triple なんて言い方をするのかな？