1.「予約でいっぱい」法
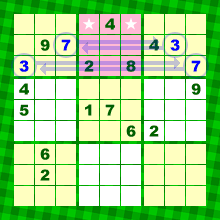
さて、図1。
ピンク色ブロック内の2つの★マス、青色の3と7に注目しましょう。
ともに横方向にレーザーを飛ばすと、3も7も★マスにしか入らないことがわかりますね。
今のところ、どちらの★に3や7が入るかはわかりません。
ただ、仮に一方の★に3が入ったとしたら、他方には自動的に7が入ることはわかりますね。
もちろん、逆に、一方の★に7が入ったとしたら、他方には自動的に3が入ることになる。
ということは、★マスには3と7以外の数字が入る余地はない ということがわかるんです。

まるで、★マスは3と7で予約いっぱいになったという状態ですね。
そういうわけで、ちょっと「3−7」とでもメモしておくことにしましょう。
ここに3と7以外は入りません。
それを踏まえて、別の数字を見てみましょう。
青色の9。
右方向へレーザー発射!
なんと。
ピンク色ブロック内で数字9が確定しちゃいました。
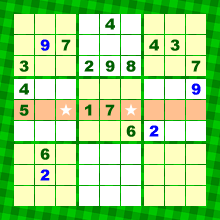
もうひとパターンやってみましょう。
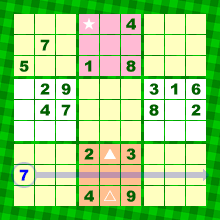
今度は、図3のオレンジ色の列を見てみます。
さらに、青色の2と9にも注目。
すると、オレンジ色の列のうち、★以外に2と9は入らないことがわかります。
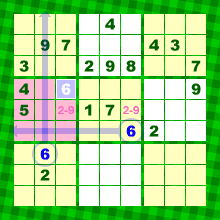
2つの★マスは「2と9で予約いっぱい」状態になりました。
「2−9」とメモしておきましょう。
そうすると、あら不思議。
青色の6からレーザーを撃てば、ピンク色ブロック内で数字6が確定しちゃいましたね。
上記の例では、3-7、2-9 のように「2個のマスに対して2個の数字の予約が確定する」ということになりました。
しかし、これは、2個に限りません。
「3個のマスに対して3個の数字の予約が確定する」でもOK。もっと言えば、マス数と数字個数が同じなら何個でもOKなのです。
2.「隠れレーザー発射!」法
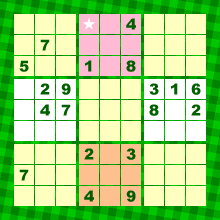
図5のピンク色のブロックに注目しましょう。
結論を先に言ってしまうと、実は★マスに7が入ることがわかるのです。
なぜでしょう?
とりあえず。
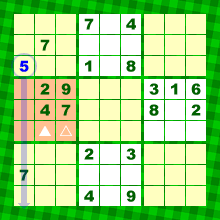
今は★マスからちょっと離れて、下のオレンジ色ブロックに注目しましょう。
青色の7から右方向にレーザーを飛ばしてみます。
そうすると、オレンジ色ブロックのうち、7が入る場所は▲か△のどちらかになりますね。
もちろん、どちらになるかは今時点では確定しません。
しかし。
▲も△も同じタテ一列上にある。
実は、ここがミソなんです。

同じタテ一列上にあるということは……、
タテ方向にレーザーを発射すればレーザーの軌跡は同じ、ということなのです。
7が▲か△のどちらに入ったとしても、そこから上方向にレーザーを飛ばすと、同じ軌跡(赤色の矢印)を描くわけです。
つまり、7の居場所はわからないんだけれど、少なくともピンク色ブロックにおいて赤色の矢印上には7は入らない ということがわかるんです。
これと、左上ブロックの7からのレーザーを考えると……。
なんと。
図5の★マスに7が入ることがわかるわけです。
もうひとつやってみましょう。
青色の5から下にレーザーを飛ばします。
すると、オレンジ色ブロックのうち、5は▲か△のどちらかに入ります。
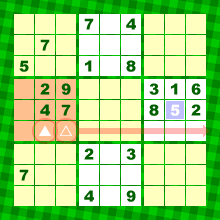
でも、どちらにしてもヨコ方向のレーザーの軌跡は同じ。
▲や△から右方向にレーザーを飛ばせば……。
赤色の矢印上には5は入らず。
右端ブロックの5が確定します。