1.数学的帰納法とは何ぞや?
今回は「数学的帰納法」を視点にパズル話をしてみようと思います。
まずは、数学的帰納法の説明から。
ご存じの方々は次セクションに進んじゃってください。
数学的帰納法。
そう。高校数学Bで習ったアレですね。
懐かしく感じた方々も多いかもしれません。
数学的帰納法とは「ある命題がすべての自然数nに対して成り立つ」ということを証明するための手法です。
具体的には、次の2つを証明しなきゃいけないのでした。
- n=1 のとき成り立つ。
- n=k のとき成り立つと仮定すると、n=k+1 のときも成り立つ。
ドえらい難しいと巷で評判(?)の数学的帰納法ですが、もぅもぅもぅ【B】でしょ😅 元凶は。
【B】を正しく理解するのがもぅ大変で大変で。
kってどっから出てきた?
なんで仮定をするの?
なんで【A】【B】の2つだけですべての自然数nで成り立つことになるの?
n=1 や n=2 で成り立っても、n=1000 くらいでエラーが起きるかもしれないじゃん!
……とまぁ、疑問が山ほど湧いて出る。
んで、理解が一向に進まない。
こういったことが数学的帰納法を難解せしめている原因かもしれません😞
とりあえず、文字kで抽象的に書いてあると【B】はわかりにくい。
【B】の言わんとしていることをkを使わずに書いてみましょう。
こうなります。
- n=1 のとき成り立つ。
- n=1 のとき成り立つならば n=2 のときも成り立つ。
n=2 のとき成り立つならば n=3 のときも成り立つ。
n=3 のとき成り立つならば n=4 のときも成り立つ。
n=4 のとき成(以下略)
※以下延々と続く。これらはすべて成り立つ。
【C】だけでは論理展開が進みませんが、これに【A】が加わると n=1 から順に論理が連鎖していくんです。
実際に n=1 のとき成り立つのだから、n=2 のときも成り立つことがわかった。
すると、実際に n=2 のとき成り立つのだから、n=3 のときも成り立つことがわかった。
すると、実際に n=3 のとき成り立つのだから、n=4 のときも成り立つことがわかった。
すると、実際に n=4 のとき成り立つのだから(以下略)
こんな感じ。
最初は【A】を適用し、後は【C】を順次繰り返す。
その結果、すべての自然数nに対して成り立つ。
こういうわけなんですね。
自然数は無限に存在するから、【C】は無限に続きます。
もちろん全部なんて書き切れない。
だから、これらを全部ひっくるめて「自然数 k のとき成り立つなら、次の数 k+1 のときも成り立つ」と書いているんですね。
kを任意の自然数として、【B】の一行で済ませているわけです。
数学的帰納法って、恐れるほどのモノではありません。
なぜなら、原理そのものは簡単だから。
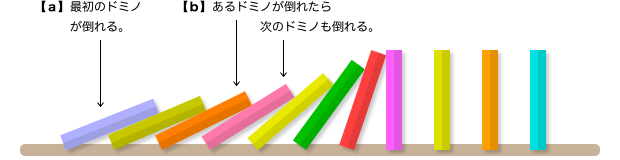
数学的帰納法なんて、ドミノ倒しと同じさ!
ドミノ倒しとは、もちろん、指先1つでバタバタ倒れるアレです。
緊張感も爽快感も達成感もヤッチマッタ感も存分に味わえる魅力的な遊びです。
このドミノ倒し、よく考えてみると、挙動はたった2種類しかないことに気付きます。
- 最初のドミノが倒れる。
- k番目のドミノが倒れたなら、k+1 番目のドミノも倒れる。(kは任意の自然数)
まず最初に指一本で【a】が起こる。
1番目のドミノが倒れたから、k=1 として【b】により2番目も倒れる。
2番目も倒れたから、k=2 として再び【b】により3番目も倒れる。
3番目も倒れたから、k=3 として再び【b】により4番目も倒れる。
以下、k=4, 5, 6, ……として【b】を繰り返し、5番目以降も順番に倒れていく。
結果、ドミノが全部倒れる。
こういう仕組みなんですね。
数学的帰納法、理解できたでしょうか?
次セクションからは、数学的帰納法を使ったパズル話を紹介しましょう。
2.ハノイの塔でこの世が終わる !?
このセクションでは、かの有名なハノイの塔の話をしましょう。
円盤をすべて移し替えるのに最短で何手かかるのか? これを数学的帰納法の視点で探ってみます。
まずは、「ハノイの塔とは何ぞや?」というところから。
2-1.ハノイの塔とは何ぞや?
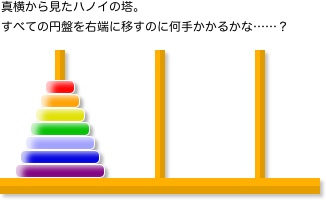
ここに3本の杭が立っている。
そのうちの一本、左端の杭に円盤がはまっている。
その円盤たちは下から大きい順に重なっていて、外観は円錐形のように見える。
ここから、この円盤たちを右端の杭にすべて移し替えたい。
しかし、次のルールを守らねばならない。
- 円盤は一度に1枚しか動かしてはならない。
- 小さい円盤の上に大きな円盤を載せてはならない。
- 円盤は必ずどれかの杭にはめなければならない。
さて、どうやって全部移し替えよう……?
これが『ハノイの塔』というパズルです。
これは円盤の枚数が多くなるほど手数がバケモノじみていくという驚異のパズルでして、そのあたりの話も最後にチョロっとしてみようかなと思います。
最初から一般的な話をしてもわかりにくいから、まずは円盤2枚の小さな塔から話を始めましょう。
2-2.小さな塔で考えよう
まず最初に、ちょいと用語を作っておきます。
円盤n枚の塔を n枚塔 と簡単に言うことにしましょう。
『ハノイの塔』とは、左端にあるn枚塔を右端にそっくり移し替えるパズルです。
まずは、円盤2〜4枚の小さな塔で考えてみましょう。
塔を左端から右端へ移し替えるのに何手かかるかな?
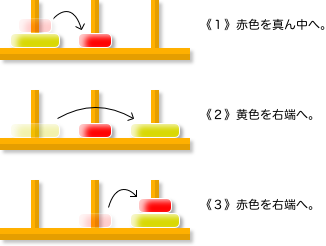
まずは2枚塔。円盤2枚の小さな塔です。
左端の塔を右端に移し替えるにはどうするか?
次の手順を踏めばOKです。
- 小円盤を真ん中に移す。
- 大円盤を右端に移す。
- 小円盤を右端に移す。
はい、できあがり。
3手でしたね。
ちなみに、この手数は 3=22-1 と表せます。
2の右肩に乗っている小さな数字「2」、2枚塔の「2」と同じですね。
2枚塔は簡単でしたね。
では、3枚塔だとどうでしょう?
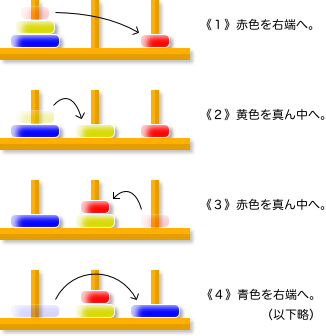
3枚の円盤を小さい方からA, B, Cとしましょう。
次の手順で移転完了です。
- Aを右端に移す。
- Bを真ん中に移す。
- Aを真ん中に移す。
- Cを右端に移す。
- Aを左端に移す。
- Bを右端に移す。
- Aを右端に移す。
今度は7手でした。
ちなみに、この手数は 7=23-1 と表せます。
2の右肩に乗っている小さな数字「3」、3枚塔の「3」と同じですね。
実は、円盤が1枚多くなった時、うまい考え方があるんです。
円盤を「一番下」と「それ以外」の2つに分けてしまう。
そうすることで、塔の移転を簡潔に捉えることができます。
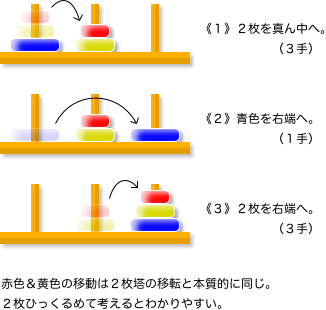
例えば、前図2-3 の7手はこう捉えましょう。
- A, Bの2枚を真ん中に退避させる。(3手)
- Cを右端に移す。(1手)
- 退避させた2枚を右端に移す。(3手)
3枚塔を移し替えるためには、どこかで円盤Cを右端に動かす必要が出てきます。
だけど、最も大きい円盤を他の円盤の上に載せてはいけないから、右端は完全に空けておかなきゃいけない。そのため、C以外の円盤(つまりAとB)をすべて真ん中に退避させなきゃいけません。
その「2枚A, Bの退避」、実は「2枚塔の移し替え」と本質的には同じ作業なんです。
ということは、2枚塔の知識があれば3枚塔の理解は簡単!
2枚塔の3手を一括りにして上記の a. b. c. へと簡略化しちゃえばいいんです。
4枚塔も理屈はまったく同じです。
3枚塔の知識を利用して、こういう手順をたどりましょう!
- 上3枚の円盤を真ん中に退避させる。(7手)
- 一番下の円盤を右端に移す。(1手)
- 退避させた3枚を右端に移す。(7手)
4枚塔は 7+1+7=15手です。
ちなみに、この「15」は 15=24-1 と表せます。
2の右肩に乗っている小さな数字「4」、4枚塔の「4」と同じですね。
2-3.一般には何手かかるのか
なんとな〜く、一般(n枚塔)の場合の手数が見えてきたかもしれませんね。
もぅ正解を言っちゃいましょう。n枚塔の場合は (2n-1) 手かかります。
これを数学的帰納法で証明してみましょう!
まずは、数学的帰納法のおさらい。
証明すべきは次の2つでした。
- n=1 のとき成り立つ。
- n=k のとき成り立つなら、n=k+1 のときも成り立つ。
これをハノイの塔に適用しましょう。
「n枚塔の移転に (2n-1) 手かかる」を数学的帰納法で証明したいなら、次の2つを証明しなきゃいけません。
- 1枚塔の移転に (21-1) 手かかる。
- k枚塔の移転に (2k-1) 手かかるなら、(k+1) 枚塔は (2k+1-1) 手かかる。
では、証明していきましょう!
まず、【A】は簡単ですね。
1枚塔の移転は1手で済みます。
そして、1=21-1 です。
よって【A】は成り立ちます。
【B】はどうでしょう?
「k枚塔の移転に (2k-1) 手かかる」と仮定して話を進めてみます。
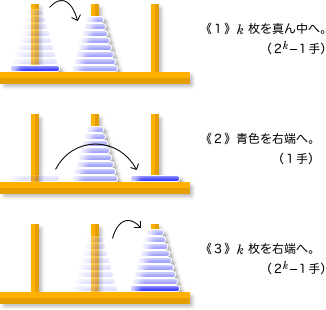
そういえば、2枚塔の知識で3枚塔の手数がわかりましたよね。
3枚塔の知識で4枚塔の手数がわかった。
……どうやらk枚塔の知識で (k+1) 枚塔の手数がわかりそうな気がする!
- 上k枚の円盤を真ん中に退避。(仮定より 2k-1 手)
- 一番下の円盤を右端に移す。(1手)
- 退避させたk枚を右端に移す。(仮定より 2k-1 手)
これで (k+1) 枚塔の移転が完了するんです。
さぁ、その合計手数は……?
= 2k+2k-1+1-1
= 2・2k-1
= 2k+1-1
おぉ〜ピッタリ!
見事、(k+1) 枚塔は (2k+1-1) 手かかるということがわかったのです。
これで【B】も証明された!
さぁ、結論です。
ハノイの塔について、数学的帰納法によりこれが証明されました。
- ハノイの塔において、左端のn枚塔を右端に移転させるのに (2n-1) 手かかる。
2-4.この世が終わる !?
最後に、ちょいと軽い小話をご紹介。
ハノイの塔がこの世に生まれたのは1883年です。
フランスの数学者・リュカによって子供向けのオモチャとして発明されました。
リュカはイタリアの数学者・カルダーノの著書『微細なる事物について』(1550年) から着想を得て「ハノイの塔」を発明したのだそう。
その書物にはこんな一節があります。
ハノイのある僧院には3本の棒を立てた黄金の台がある。
その1番目の棒には64枚の黄金の円盤が降順に──最大の円盤が最下部に、最小の円盤が最上部に──はめ込まれている。
僧たちは、降順にそれらを保ったままで1回に1枚ずつ動かして3番目の棒にすべての円盤を移し替えよとの神命を受けている。
ただし、より大きな円盤をより小さな円盤の上においてはならない。3本の棒はすべて使用できる。
僧が最後の円盤の移し替えが終わるときこの世は終わるのだという。
なぜか?『世界でもっとも美しい10の数学パズル』p.156 より
この世が終わるだなんて、まぁ大げさな😅
いや、まぁたしかに 64枚は多いけどさ😅
しかし、この後、これは大げさな話ではなかったのだとわかります。
実は、この世が終わるどころの話ではないんです。
神命通りに円盤の移し替えを終えるには、僧たちは円盤を (264-1) 回も移動させなければなりません。
はて、264-1 ってどれほどの数なんだ?
264-1 = 18446744073709551615
うっわ😅
1844京ですって😅
どんくらいの数だかまったく想像つかねぇよ😅
いやぁすごい数だ。
円盤を1秒に1回動かしたとしても1844京秒かかるんだもの。
この1844京秒、どれくらいの長さなんでしょう?
「1年=365日=31,536,000秒」と閏年を無視して、およその年数に換算してみましょうか。
18446744073709551615 ÷ 31536000 = 約 584942417355
5849億年😅
そりゃぁこの世が終わるのも当然だ😅
ちなみに、宇宙の誕生・ビッグバンはおよそ138億年前に起こったとされています。
宇宙の歴史って、たった138億年しかないんだぜ!
仮にビッグバンと同時に僧たちが円盤を動かしてきたとしても、皆さんが当ページを見ている時点では神命の 2.3%ほどしか進んでいないのです。
64枚の移し替えがどれほど想像を絶する苦行なのか。形容する言葉はこの世にはなさそうだ。
僧たちが神命を遂げた時、この世が終わることはおそらく間違いない。
いや、「終わる」ではなく「終わっている」が正しいか。
地球や太陽なんてとうの昔に宇宙の藻屑だ。宇宙そのものが終わっていても不思議ではないのです。
3.穴あきチェス盤にブロックを敷き詰められるか?
次は、チェス盤の話をしましょう。
こんな問題を考えてみます。
3-1.穴あきチェス盤の問題
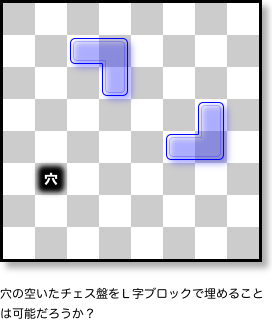
8×8マスのチェス盤がある。
この盤には64マスあるが、そのうち1マスに穴が空いている。
そして、このチェス盤と一緒にブロックがたくさん用意されている。
そのブロックはL字型をしていて、ちょうどチェス盤の3マスを覆うことができる。
今、このチェス盤にL字ブロックを敷き詰めたい。
ただし、次のルールを守らねばならない。
- ブロックはマスに沿って置かなければならない。
- ブロックを重ねてはならない。
- ブロックで穴を塞いではならない。
要は「穴以外の63マスをL字ブロック21個で覆い尽くせるだろうか?」という問題です。
果たして、それは可能なんだろうか?
それとも、穴の位置によっては不可能だったりするんだろうか?
いや、どこに穴があっても可能なんだろうか……?
もぅ正解を言っちゃいますが、実は、8×8盤面のどこに穴があってもL字ブロックを敷き詰めることは可能です。
ただ、ここではさらに話を広げます。
次のことを考えてみたい!
一辺のマス数が 2n であるチェス盤がある。
その盤面から任意に1マスを選び、そこに穴を空ける。
そして、そのチェス盤と一緒にブロックをたくさん用意する。
そのブロックはL字型をしていて、ちょうどチェス盤の3マスを覆うことができる。
今、穴を塞がないようにこのチェス盤にL字ブロックを敷き詰めたい。
どこに穴があったとしても、それは可能なんだろうか……?
「一辺が 2n マス」と話が広がりました。
2×2, 4×4, 8×8, 16×16, 32×32, ……といった諸々のサイズの穴あきチェス盤を考えるわけですね。
どのサイズでも、かつ、どこに穴があってもL字ブロックを敷き詰めることは可能なんだろうか?
それを考察していきます。
最初から一般的な話をしてもわかりにくいから、まずは小さなサイズから話を始めましょう。
3-2.小さなチェス盤で考えよう
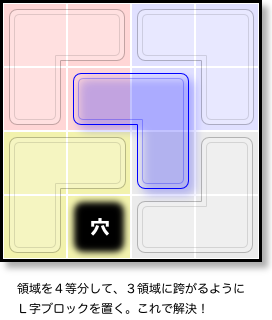
2×2サイズは言うまでもないので、4×4サイズから話をします。
穴の空いた4×4チェス盤、L字ブロックでどう埋めればいいのか?
次の手順を踏めばうまくいきます。
- 盤面を2×2サイズの小領域に4等分する。
- 穴のない3領域に跨がるようにL字ブロックを置く。
- あとはブロックで埋めるだけ。
実は、手順 2. が大きなカギです。
これ1つだけで、もぅ4×4サイズは完全解決したも同然なんです。
なぜかと言うと、こうなったから。
手順 2. で置いたブロックを穴だとみなすと、小領域はすべて「穴の空いた2×2チェス盤」になった。
まるで 図3-2 の青色ブロックが穴の役割を果たしたかのよう。
そのおかげで、あとは小領域それぞれの問題に帰着するんです。
実は、穴がどの位置にあろうとも、上記 1.〜3. で済みます。
よって、4×4の場合、穴の位置にかかわらずL字ブロックを敷き詰められるんです。
4×4サイズは肯定的に解決できましたね。
では、8×8サイズはどうでしょう?
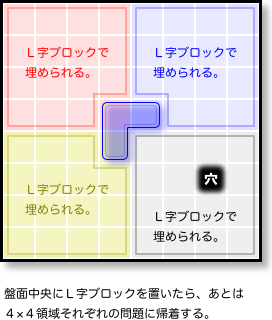
8×8の場合はこうしましょう。
- 盤面を4×4サイズの小領域に4等分する。
- 穴のない3領域に跨がるようにL字ブロックを置く。
- あとはブロックで埋めるだけ。
ここでも手順 2. は大きなカギです。
これ1つだけで、8×8サイズも攻略完了です。
なぜかと言うと、こうなったから。
手順 2. で置いたブロックを穴だとみなすと、小領域はすべて「穴の空いた4×4チェス盤」になった。
4×4サイズについては 前図3-2 で説明したばかり。
つまり、4つの小領域はすべてL字ブロックで埋めることができる。
結果、8×8の場合も穴の位置にかかわらずL字ブロックを敷き詰められるんです。
8×8サイズも肯定的に解決できましたね。
さて、図3-2 と 図3-3 の解説を読んで、もぅ気付いた方々は多いかも知れませんね。
そうです。話がまったく同じなんです。
4等分して、L字ブロックが跨いで、残りを埋める。
これだけ。
ということは、16×16サイズも同じく解決できそうですね。
- 盤面を8×8サイズの小領域に4等分する。
- 穴のない3領域に跨がるようにL字ブロックを置く。
- あとはブロックで埋めるだけ。
8×8サイズについては 図3-3 で説明したばかり。
これで16×16サイズもOKです!
3-3.一般のチェス盤の場合
なんとな〜く、一般(サイズ 2n)の場合も攻略方法が見えてきたかもしれませんね。
もぅ結論を言いましょう。どのサイズであっても、かつ、どこに穴があっても肯定的に解決できます。
それを数学的帰納法で証明してみましょう!
再び数学的帰納法のおさらい。
証明すべきは次の2つでした。
- n=1 のとき成り立つ。
- n=k のとき成り立つなら、n=k+1 のときも成り立つ。
これを穴あきチェス盤に適用しましょう。
「サイズ 2n のどんな穴あきチェス盤も必ずL字ブロックを敷き詰められる」を数学的帰納法で証明したいなら、次の2つを証明しなきゃいけません。
- サイズ 21 のどんな穴あきチェス盤も必ずL字ブロックを敷き詰められる。
- サイズ 2k のどんな穴あきチェス盤も必ずL字ブロックを敷き詰められるなら、サイズ 2k+1 も敷き詰められる。
では証明していきましょう!
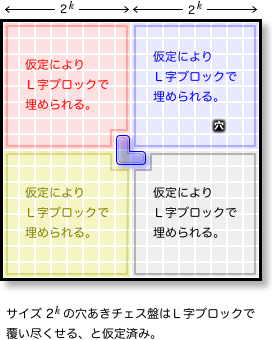
まず【A】は明らかすぎて言うまでもありません。
では【B】はどうでしょう?
「サイズ 2k のどんな穴あきチェス盤も必ずL字ブロックを敷き詰められる」と仮定して話を進めます。
そういえば、2×2サイズの知識で4×4サイズを解決できましたね。
4×4の知識で8×8も解決できた。
もしかしたら、サイズ 2k の知識でサイズ 2k+1 を解決できそうかな?
- サイズ 2k+1 の盤面をサイズ 2k の小領域に4等分する。
- 穴のない3領域に跨がるようにL字ブロックを置く。
- あとはブロックで埋めるだけ。(仮定により必ず埋められる)
仮定のおかげで、どの小領域もL字ブロックで埋められます。
よって、サイズ 2k+1 の盤面全体も埋まるんです。
というわけで【B】も証明されました!
さぁ、結論です。
穴あきチェス盤について、数学的帰納法によりこれが証明されました。
- サイズ 2n のどんな穴あきチェス盤にも必ずL字ブロックを敷き詰められる。
無事解決!
3-4.まるで石畳だね!
最後に、「ちょっとやってみた」系の話を。
あるサイズ 2n の穴あきチェス盤にL字ブロックを敷き詰めたいなら、その半分のサイズ 2n-1 に遡ると良いでしょう。
そのサイズのおかげで、サイズ 2n が解決できるわけですもんね。
もちろん、サイズ 2n-1 も同様で、さらに半分のサイズ 2n-2 に遡ると良い。
これを繰り返せば、最終的に2×2サイズにまで遡ります。
そして、2×2サイズは簡単に敷き詰められる。
その後、今度は倍々……と戻っていけばサイズ 2n が完成しますね。
どのサイズ 2n も可能だとわかった今、実際に敷き詰めてみたいと考えるのが人情というもの(?)
というわけで、とあるサイズに挑戦してみました。
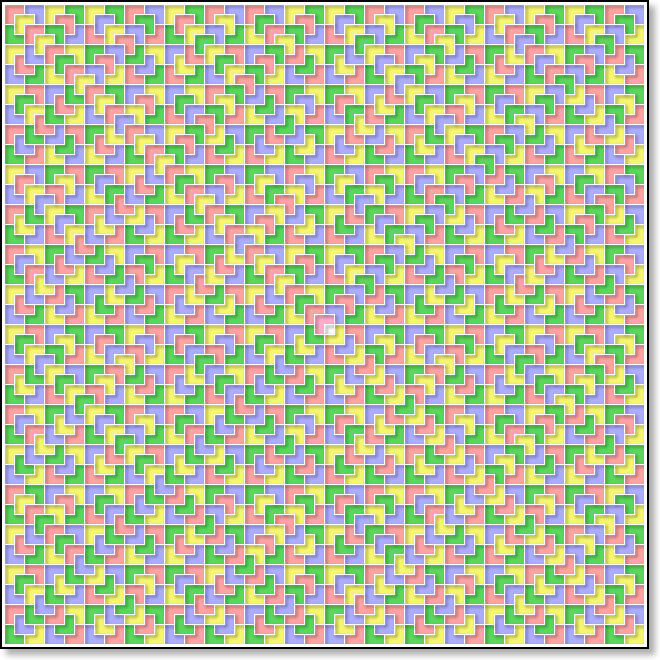
64×64サイズ!
どうですか! この1365個のブロックたち!
どっかの広場とかに行けば、こんな石畳がありそうだ😅
画像はわざとカラフルにしてみました。
綺麗でしょぉ〜🥰
いやぁもぅ、これだけブロックを敷き詰めたのなら『4色問題』を考えたくなるのさ!
同じ色が辺で接しないよう色分けする。これもまたパズル。
さらに頂点でも接しないように色分けしてみました。
この画像を作っててメッチャ楽しかった😃
参考・参照
- マーセル・ダネージ 著/寺嶋英志 訳, 青土社,『世界でもっとも美しい10の数学パズル』(第3刷), 2007
更新履歴
- 2022. 5.26.
- 新規公開。