1.こんなパズル問題がありましたっけ
いわゆる「頭の体操」系と呼ばれるパズルには、方角を利用した物が存在します。
例えば、こ〜んなヤツ。
ある地点Aから南に 1km 歩き、そこから東に 1km、続いて北に 1km 歩いてみた。
そうしたら、なぜか元の地点Aに戻っていた!
こんなことって起こり得るんだろうか?
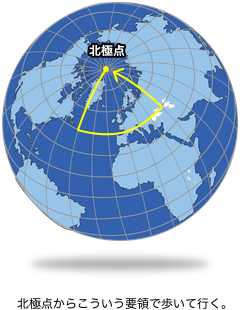
正解の一例は 図1-1 です。
地点Aは北極点だった。
そこからスタートすると、三角形を描いて元の地点に戻る。
こういうわけです。
(図のルートが 1km より長いですが、そこはツッコまないでください😅)
そうか、北極点があったね!
北極点では 360° すべての方角が南だし、逆に、他の地点から北極点に向かう方角はすべて北ですもんね。
だから、北極点から歩けば元に戻れるんですね。
頭の体操系のパズルは、時折こういう並外れた発想に触れられるから面白い。
身の回りレベルの小さな発想では、正解は思い付かない。
こういった問題はスケールの大きさも魅力です。
なんだったら、すぐさま解答を見てその発想に感心しちゃってもいい。
それもひとつの面白さです😊
……と書いたところで、ふと「あれ? 北極点って、海の上になかったっけ?」と気が付いた。
気になって、ちょいと調べてみました。
たしかに北極点は北極海の海上にある。けれど、海面が年中凍っているという!
海に浮かんだ氷の床、「海氷」と呼ばれる物ができているんですね。
サイト『JAMSTEC BASE』によると、冬場だと氷の厚さは 数メートル。場所によっては20メートルを超えるらしい!
だから、北極点は陸の上にあるようなもの。上述の正解は現実でも可能と言えそうです。
あーよかった😅
「北極点は海の上だから歩けねーよw」とかいうツッコミが来たらどうしようかと思ってた😅
もう1問、紹介しましょう。
こ〜んな問題。
ある場所に2人が並んで立っている。
そこから同じ方角に同じ速度で2人がしばらく歩いていくと、なんと、20,000km も離れてしまった!
こんなことって起こり得るんだろうか?
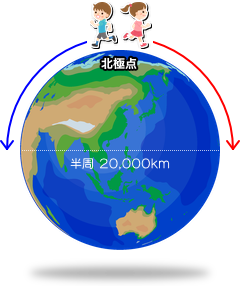
正解の一例は 図1-2 です。
2人は北極点にいて、それぞれ正反対の方向に真っ直ぐ進んでいきました。
で、2人とも赤道にたどり着いた時、2人の(赤道に沿った)距離は 20,000km になっていた(赤道は一周 約40,075km です)。
こういうわけです。
この問題は南極点がカギです。
子午線に沿って南極点に向かう方角はすべて南なんですね。
普通に考えたら、2人の距離なんて変わるわけがありません。
ところが、地球レベルだと2人の距離は自由自在になる。
前問と同じで、発想のスケールだけでこうも結果が違うという、面白いパズルなんですね。
あっ。
この問題は海の上を歩かないと実現できないですね😅
「海の上は歩けねーよw」とかいうツッコミはどうかどうか勘弁してください😅
2.どんなに風が吹こうとも、どこ吹く風の場所がある
北極点と南極点では方角が通常とまったく違う。
これは皆さん既にご存じでしょうけれど、パズルという形であらためて認識できるのもまた面白いものです。
次は、パズル以外の例で方角の不思議さを語ってみます。

我々の住んでいる地球には地軸があり、それを基に子午線(経線)と緯線が設定されていますね。
それにより、北極点と南極点が存在します。
さて。
皆さん、神様になったつもりで、ちょいと地球に風を起こしてやりましょうか!
図2-1 のように、世界中のあらゆる地点で同じ方向・同じ速度の風を起こす。
どうだ、地球の人間共! 南からのそよ風に抱かれて心地良いだろう!
ところが。
全人類が快感に浸っている中、風の恩恵を受けられない地点が2カ所できてしまいました。
北極点と南極点。この2つです。
風は子午線に沿って上へ上へと移動するから、どうしてもてっぺんに風が集中してしまう。
全方向から北極点に風が押し寄せて、風の力を打ち消し合って無風になるんです。
南極点では逆に風が放射状に発散して、同じく無風です。
風を起こしても、風の吹かない場所ができあがる。
神といえど、すべての地点で同時に風を起こすことは叶わないのかもしれない。
あぁ、神は全知全能ではないということか。
この話、実は、前セクション1のパズルと本質的に同じです。
要は何を言いたいのかというと、こういうことなんです。
- 地球には、通常の方角(東西南北)を設定できない地点が存在する。
地軸を基準にした方角の設定は、科学的に自然であり有用だと言えるでしょう。
地理的な視点で見ても、地球上のほぼ全域で東西南北を認識できるのは便利だし。
だけど、方角に関して特異な2点がどうにも生じてしまい、その特異性はおそらく消せそうにないんですね。
仮に地軸を完全無視して独自の方角を無理やり設定しようとしても、たぶん、特異点はどこかに発生してしまう気がする……。
そこで、疑問を1つ投げてみる。
この特異性は絶対に除去できないんだろうか?
つまり、「地球上のすべての地点で東西南北を設定する」ことは不可能なんだろうか?
球面と方角の関係性。
このことについて、数学の視点でちょいと探ってみたい。
3.数量を気にしない幾何学で大活躍するあの数値
トポロジー。
これは何かと言うと、枝葉の情報をすべて排除して図形や空間の持つ本質を研究する数学分野です。
なんか説明がわかりにくい。ええい、もぅ引用しちゃえ😅
トポロジーでは、「伸ばしたり、縮めたり、曲げたり、ゆがめたりして重ねられるものは同じもの」と見なします。トポロジーがゴム膜の幾何学といわれる所以です。
たとえば、円や、三角形や、四角形はすべて同じものと見なしますし、ドーナツとコーヒーカップも同じものと見なします。
(中略)
そして、このような変形にもかかわらず、共通に備えている図形(空間)の性質を探ろうというのがトポロジーです。もっと具体的にいえば、図形の各辺の長さとか、曲がり具合とか、面積とか、角度といった目につきやすい部分の情報を取り去り、その図形の裏に隠された根源的な本質を見極めることにあります。いってみれば、「量を捨象して質に注目」することであり、もっといえば「数量的世界観の超克」ということです。
(中略)
トポロジーの発想をひとことで表わせば、物事の枝葉末節を取り去り、その本質を見極めるというものです。『トポロジーの発想』p.6 より
何らかの情報を伝える時、些末な情報を切り捨て、本質情報を際立たせるという考えはとても大事です。
例えば、鉄道の路線図は当駅を中心として周辺駅との繫がりがわかれば良い。だから、日本地図通りの正確な図は必要ありません。
駅間の距離や線路の物理的形状などをバッサリ捨象して、簡素な路線図になっている。
そして、駅同士の繫がりは捨象せず、路線図の本質情報を際立たせているわけです。
本質と枝葉を切り分け、本質部分を追究していくのがトポロジーという学問です。
まぁ、あんまり難しく考えず、引用文のゴム膜のように「ナンボでも自由に伸び縮みする軟らかいゴムで物体ができている」と捉えると理解しやすいかもしれませんね。
切り貼りしないで変形できれば同じ物とみなす。こういう解釈でOK!
トポロジーではこれを 位相同型 または 同相 と言います。
ドーナツとコーヒーカップは同相なんですね。
同相の例をもうひとつ挙げましょう。
皆大好き正多面体!
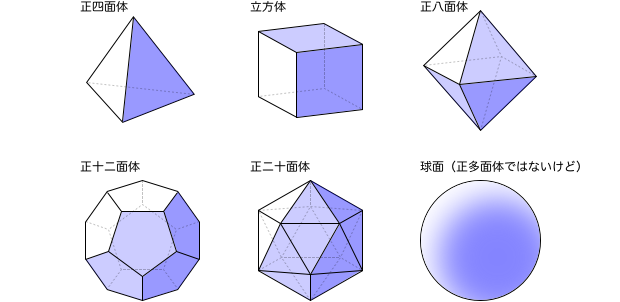
正多面体は全部で5種類あるけれど、これらは球面と同相です。
尖っているカドを丸めて面を膨らませば、球面になりますもんね。
さらに言うと、この6つはすべて同相です。
このトポロジーの世界、実は、至宝とも言える「ある数値」が存在します。
それは、オイラー標数です。
この世にはさまざまな立体があるけれど、それらは「面・辺・頂点」が繋がって形成されていますよね。
この3種類の要素を使った、すごく簡単な数値が定義されているんです。
頂点・辺・面のみで構成される(中身の詰まっていない)3次元立体に対して、次の式の値を オイラー標数 と呼ぶ。
ここで、正多面体と球面のオイラー標数をちょいと求めてみましょうか!
それぞれ頂点・辺・面の個数を数えて計算します。
さぁ結果はどうなるか……?
| 頂点 | 辺 | 面 | オイラー標数 | |
|---|---|---|---|---|
| 正四面体 | 4 | 6 | 4 | 4-6+4 = 2 |
| 立方体 | 8 | 12 | 6 | 8-12+6 = 2 |
| 正八面体 | 6 | 12 | 8 | 6-12+8 = 2 |
| 正十二面体 | 20 | 30 | 12 | 20-30+12 = 2 |
| 正二十面体 | 12 | 30 | 20 | 12-30+20 = 2 |
| 球面 | 1 | 1 | 2 | 1-1+2 = 2 |
マジか!
全部同じ値になった!
まるで示し合わせたかのように2が並ぶ。
もはや偶然としか思えない😅
驚愕の結果です。
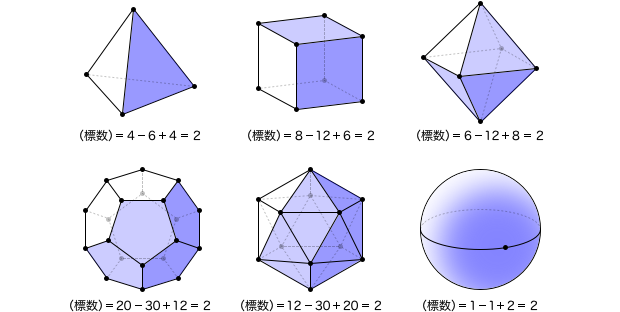
もちろん、これは偶然なんかではありません。
このオイラー標数、実は、とんでもなく有能なシロモノでして。
こういう定理があるんです。
- 2つの立体が同相ならば、オイラー標数も等しい。
正多面体と球面はすべて同相であった。
ということは、オイラー標数もすべて等しくなる。
実際、定理通りに同じ値になりました。
ちなみに、これは『オイラーの多面体定理』という名前で知られています。
この定理はオイラー標数に関するほんの一部にすぎず、トポロジーにおいてオイラー標数の果たす役割は相当に大きいようです。
トポロジーの中心的存在と言えるかもしれませんね。
オイラー標数、恐るべき子だった!
さて。
オイラー標数を説明したところで、セクション2の風の話をちょいと思い出しましょう。
「地球上に南風を起こしても静止点(無風の地点)が存在する」のでした。
この話、実は、オイラー標数が深く関係しています。
トポロジーの有名な『不動点定理』とタッグを組んで、こ〜んな定理が存在するんです。
- ある立体のオイラー標数が0以外の時、必ず静止点が生じてしまう。
逆に、オイラー標数が0の時、静止点のない流れが存在する。
地表面のオイラー標数は2です。0ではない。
ということは、地球上のすべての地点に南風を起こすことは不可能なんですね。
どんなに頑張っても静止点は絶対に無くせないのだから。
もっと言うと、たとえ風の方向が場所によってバラバラであったとしても、静止点は地球上のどこかに必ず存在します。
「オイラー標数が0ではない」という事実が静止点の存在を完全に保証しちゃっているんです。
方角の話で言うと、地球上のすべての地点で東西南北を設定するということは叶わぬ夢となりました。
静止点ではどうしても方角にバグが起こる😅
そんなわけで、地球には方角に関する特異点が必ず存在します。
仮に現在とは異なる方角が定義されたとしても、地表面が球面である限り、セクション1のようなパズル問題は必ず成立します。
地球の仕様が方角パズルの面白さを保証してくれているんですね😊
最後に、しょーもない話を1つ。
国立科学博物館というサイトの『宇宙の質問箱』というページによると、天王星の地軸は約98° 傾いているそうです。
天王星はほぼ横倒し。
もし地軸を基に東西方向を設定して勝手に天王星に方角を定義したとしたら、こ〜んなパズル問題ができたりするのかな?
ある地点Aから西に 1km 歩き、そこから南に 1km、続いて東に 1km 歩いてみた。
そうしたら、なぜか元の地点Aに戻っていた!
こんなことって起こり得るんだろうか?

この場合だと、地点Aは東極点なんて呼ばれたりするんだろうか……?
まぁ私の勝手な妄想だけれども😅
4.あのゲームの世界では、み〜んな平等に心地良い
ここからは余談です。
今までの話を聞いて、地球全域に淀みなく風を起こすことは不可能だとわかりました。
じゃぁ、今度は逆の視点に立って、こ〜んな疑問を投げてみましょうか。
全域に淀みなく風を起こせる地形って……あるのかな?
どういう地形なら静止点のない風を起こせるか?
言い換えると、「オイラー標数が0である立体はあるんだろうか?」ということです。
結論を言うと、そういう立体は存在します。
数学では「トーラス」と呼ばれている物で、浮き輪に例えられることの多い立体です。
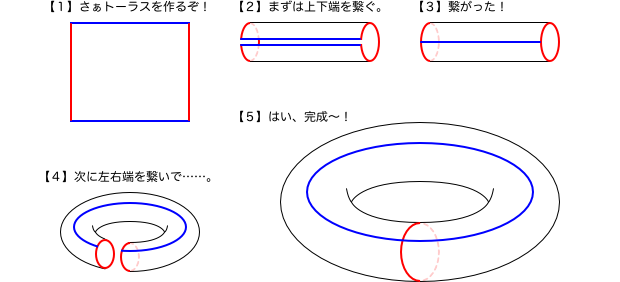
ここで、いきなりですがトーラスの作り方を説明しましょう!
まず、長方形を1つ用意します。
今、この長方形の上下端は繋がっているものとしましょう。同様に、左右端も繋がっているものと考えます。
つまり、上端を通過して外に出た人間は下端から現れ、右端を通過して外に出た人間は左端から現れる。そういう仕組みです。
繋がっているのなら物理的にくっつけても差し支えないので、下図のように実際にくっつけてみましょう。
こうしてできあがった立体がトーラスです。
まさに浮き輪!
さて。
この特殊な長方形、実は、ゲーム好きな方々にはお馴染みのアレと同じなんです。
そのアレとは何か?
それは、ドラクエのマップです。
なんと、我々の住む地球とは違って、ドラクエの大地はトーラスの形をしていた!
歴代の勇者たちは浮き輪の上で竜王やハーゴン、バラモスなんかを倒してきたわけです😅
マップからはまったく想像がつかん。でも、これは紛れもない事実。
ドラクエ史にも記載されていないであろう、隠れた真実である! ……かな?😅
このトーラス、オイラー標数は0です。
ということは、静止点のない風を起こせるはず。
もう一度神になったつもりで実際に起こしてみましょうか!
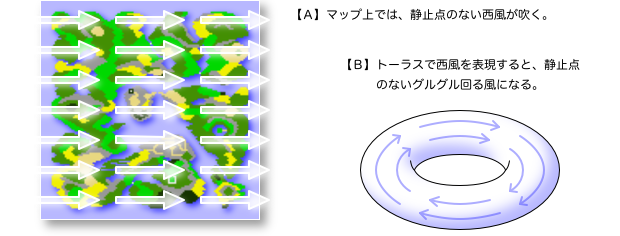
おおぉ! すべての場所に西風が起きた!(上図【A】)
左右端は繋がっているから、風は循環しています。
これをトーラス上で表現すると、上図【B】のようにグルグル流れていく感じ。
まるでそうめん流し器のように、そよ風が吹くわけです。
ドラクエの大地には、すべて平等に風が吹く。
ラダトームも、竜王の城も、ローレシアも、ハーゴンの城も、アリアハンも、バラモス城も、ロザリーヒルも、み〜んな平等だ。
もちろん、ドラクエに限らない。ファイナルファンタジーも他の RPG もみ〜んな平等。
住民たちは皆、同じ風に抱かれて心地良く時を過ごせるのです。
なんて平和な世界なんだろう🥰
参考・参照
- 川久保勝夫 著, 講談社,『トポロジーの発想』(第8刷), 2008
- 国立研究開発法人・海洋研究開発機構, 『JAMSTEC BASE』,
「真の北極点で写真を撮るのが困難」なワケ…多くの人が知らない、北極研究“現場あるある”の中身―私たちの知らない北極,
https://www.jamstec.go.jp/j/pr/topics/jamstec-eye-20230925/, (参照 2024. 2. 8.) - 国立科学博物館, 『宇宙の質問箱』,
https://www.kahaku.go.jp/exhibitions/vm/resource/tenmon/space/, (参照 2024. 2.20.)
更新履歴
- 2024. 2.22.
- 新規公開。