1.どういう解法?
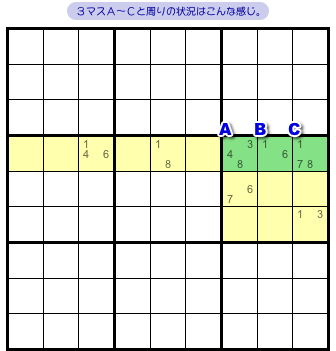
図1-1、緑色の3マスA〜Cに注目しましょう。
そして、A〜Cすべてが属する列とブロックも見てみます。
黄色部分で、マスは12個ありますね。
その中に、次の2つを満たすマスがチラホラあります。
- 候補数字を2〜3個しか持っていない。
- その2〜3個の内訳は、A〜Cの中から0〜1個ずつ抽出したものである。
さぁ、こういう状況でどういうふうに Aligned Triple Exclusion を使っていくんでしょう?
……ていうか、2番目の条件がわかりづらい😓
以下の解説を読んだ後なら理解し易いかも。
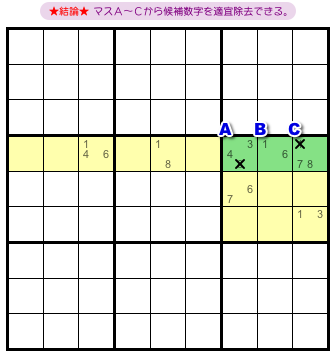
さて、図1-1 からはどういう結論が得られるんでしょう?
こうなるんです。
- 黄色マスの候補数字に応じて、3マスA〜Cから候補数字を適宜除去できる。
図1-1 の場合だと、2マスA, Cに候補数字の除去が起こります(図1-2)。
マスAから候補数字8を除去できます。
マスCから候補数字1を除去できます。
なぜ、こういう結論になるんでしょう?
以下で説明しましょう。
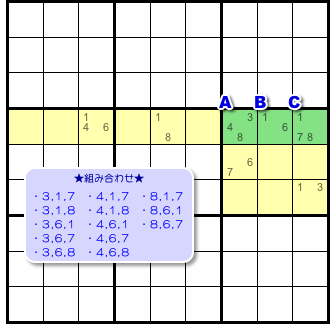
3マスA〜Cに入る数字の組み合わせを列挙してみましょう。
- 3と1と7。
- 3と1と8。
- 3と6と1。
- 3と6と7。
- 3と6と8。
- 4と1と7。
- 4と1と8。
- 4と6と1。
- 4と6と7。
- 4と6と8。
- 8と1と7。
- 8と6と1。
- 8と6と7。
うゎ、13通り😅
多すぎて気が滅入る😵
マスや候補数字が多いとネズミ算式に増えてくよね……。
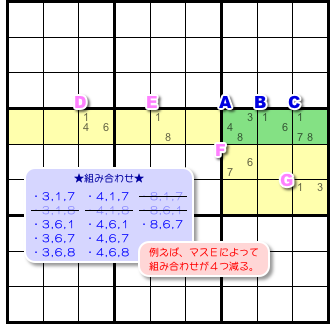
ところが!
実は、ここから組み合わせを除外できるんです。
まずはマスD。
候補数字は1, 4, 6ですね。
ということは、その3つ全部を含む組み合わせを除外できます。
なぜなら、それを採用するとマスDに入る数字がなくなっちゃう😣
「4と6と1」が該当します。
次はマスE。
候補数字は1, 8ですね。
ということは、1と8を含む組み合わせをすべて除外できるんです。
「3と1と8」など4つあります。
理由は同様です。
それらを採用するとマスEに入る数字がなくなっちゃうから。
マスF, Gも同様です。
6と7を含む組み合わせもすべて除外できます。
1と3を含む組み合わせもすべて除外できます。
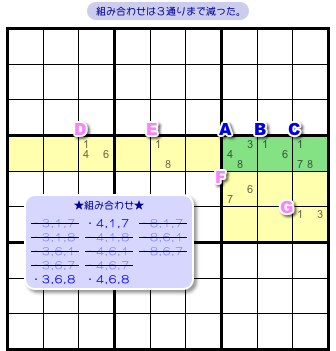
さぁ、組み合わせはどれだけ除外されたんでしょう?
除外された組み合わせを薄い色で表してみます。
- 3と1と7。 ※マスGによりダメ
- 3と1と8。 ※マスEまたはGによりダメ
- 3と6と1。 ※マスGによりダメ
- 3と6と7。 ※マスFによりダメ
- 3と6と8。
- 4と1と7。
- 4と1と8。 ※マスEによりダメ
- 4と6と1。 ※マスDによりダメ
- 4と6と7。 ※マスFによりダメ
- 4と6と8。
- 8と1と7。 ※マスEによりダメ
- 8と6と1。 ※マスEによりダメ
- 8と6と7。 ※マスFによりダメ
うゎ、ずいぶんと除外された😓
想像以上にマスD〜Gが働いてくれました。
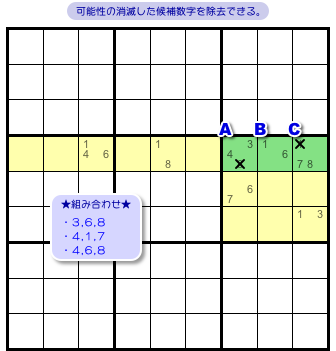
さて、残った3通りから何が言えるんでしょう?
- 3と6と8。
- 4と1と7。
- 4と6と8。
こういうことが言えるんです。
- マスAには数字3, 4しか可能性がない。
- マスCには数字7, 8しか可能性がない。
なんと、2マスA, Cに入り得ない数字が生じちゃったんです。
マスAに数字8の可能性はなくなった。
マスCに数字1の可能性はなくなった。
というわけで、結論はこうなります。
- マスAから候補数字8を除去できる。
- マスCから候補数字1を除去できる。
これが、図1-2 で示した結論です。
2.実際に使ってみよう!
次は、実際の盤面で Aligned Triple Exclusion を使ってみましょう。
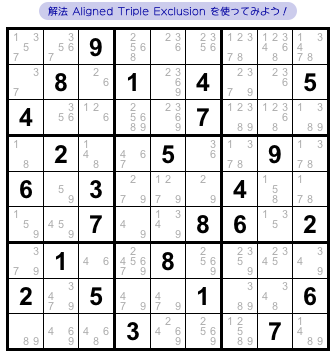
図2-1 では、とあるマスから候補数字を除去できます。
それを解法 Aligned Triple Exclusion で突き止めてみます。
この解法を使うためには、ある列&ブロックを1個ずつ見つけ、その交差領域の3マスに注目しなければいけません。
さぁ、それはどこにある……?
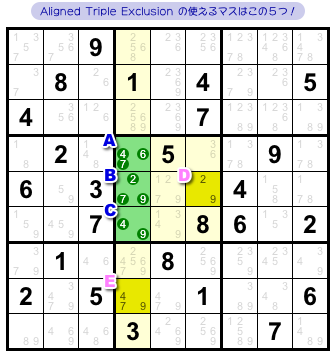
ここにありました!(図2-2)
3マスA〜C、そして、その周りには2マスD, E。
マスD, Eはどちらも次の2つを満たしています。
- 候補数字を2〜3個持っている。
- その2〜3個の内訳は、A〜Cの中から0〜1個ずつ抽出したものである。
この5マスはこういう状況になっています。
ここから話は始まります。
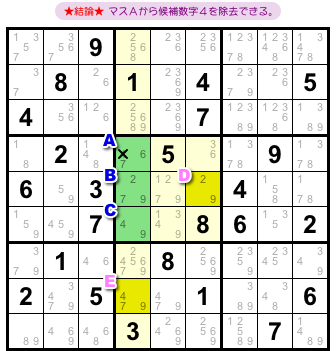
この場合の結論はこうなります。
- マスAから候補数字4を除去できる。
理由は以下の解説でわかります。
マスAに数字4の入る可能性がなくなっちゃいます。
では、解説していきましょう。
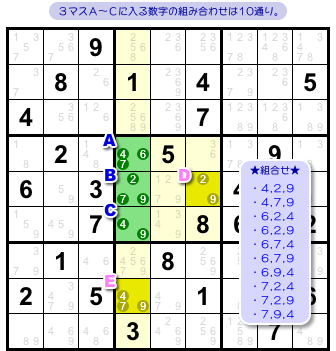
3マスA〜Cに入り得る数字の組み合わせを列挙してみます。
以下の10通りですね。
- 4と2と9。
- 4と7と9。
- 6と2と4。
- 6と2と9。
- 6と7と4。
- 6と7と9。
- 6と9と4。
- 7と2と4。
- 7と2と9。
- 7と9と4。
やっぱ多い😅
ただ、4とか7とか9とか、同じ数字が複数あると組み合わせが少なくなりますね。
それがちょっとだけ救い。
ここから、2マスD, Eのおかげで組み合わせはいくつか除外されていくことになります。
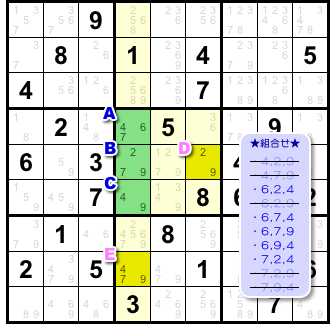
マスDの候補数字は2, 9ですね。
ということは、2と9を含む組み合わせをすべて除外できます。
マスEの候補数字は4, 7, 9ですね。
この場合,4, 7, 9すべて含む組み合わせを除外できます。
- 4と2と9。 ※マスDによりダメ
- 4と7と9。 ※マスEによりダメ
- 6と2と4。
- 6と2と9。 ※マスDによりダメ
- 6と7と4。
- 6と7と9。
- 6と9と4。
- 7と2と4。
- 7と2と9。 ※マスDによりダメ
- 7と9と4。 ※マスEによりダメ
組み合わせが半分に減りました😊
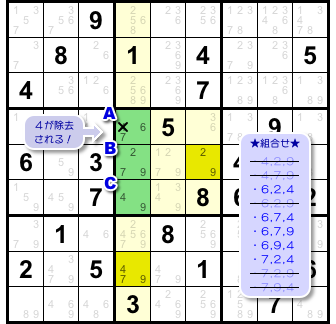
さて、残った組み合わせを見てみましょう!
- 6と2と4。
- 6と7と4。
- 6と7と9。
- 6と9と4。
- 7と2と4。
なんと、マスAに入り得る数字は6, 7だけになってしまいました。
4の入る可能性が消えちゃったんですね。
というわけで、マスAから候補数字4を除去できます。
図2-3 の結論通りになりました😄
3.align してないのに Aligned?
今までのセクションでは、3マスA〜Cは一列に並んでいましたね。
本来、Aligned Triple Exclusion は「一列に並んだ3マスの候補数字が除去される」という解法なんです。
文字通り「Aligned Triple」ですもんね。
ところが、とある事実が判明したんです。3マスは一列に並んでいなくても良いというのです!
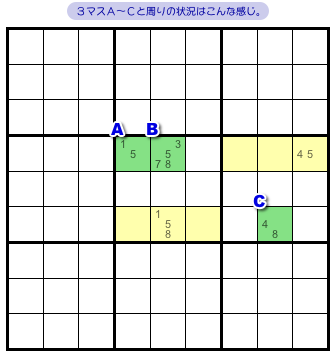
図3-1 の盤面には3マスA〜Cがあります。
が、今までとは違って一列には並んでいません。
non-aligned triple ですね!
そして、マスA〜Cすべてと列やブロックを共有しているマスがいくつかあります。
黄色部分で、6個ありますね。
その中に、次の2つを満たすマスがチラホラあります。
- 候補数字を2〜3個しか持っていない。
- その2〜3個の内訳は、A〜Cの中から0〜1個ずつ抽出したものである。
こういう状況だったとしましょう。
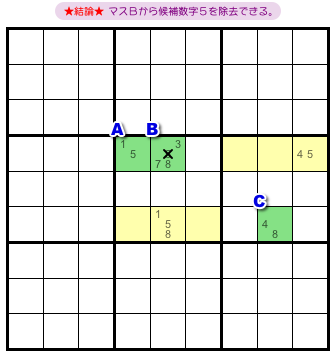
結論はこうなります。
- マスBから候補数字5を除去できる。
理由は同じです。
以下で簡単に説明しましょう。
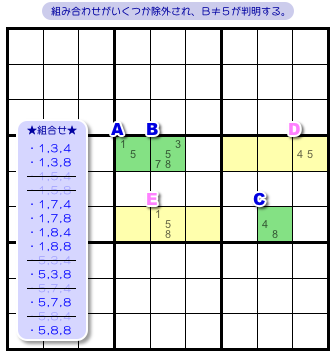
3マスA〜Cに入る数字の組み合わせは14通り。
しかし、そこから5つを除外できます。
- 1と3と4。
- 1と3と8。
- 1と5と4。 ※マスDによりダメ
- 1と5と8。 ※マスEによりダメ
- 1と7と4。
- 1と7と8。
- 1と8と4。
- 1と8と8。
- 5と3と4。 ※マスDによりダメ
- 5と3と8。
- 5と7と4。 ※マスDによりダメ
- 5と7と8。
- 5と8と4。 ※マスDによりダメ
- 5と8と8。
残った組み合わせを見ると、マスBに数字5の入る可能性はなくなってしまいました。
こんなふうに、3マスが align(整列)していなくても同じ理屈が成り立っちゃう。
こういうパターンもあるんですね。
この場合の解法には固有の名前がついていないようですが、「Subset Exclusion」と呼ぶことがあります。
Subset Exclusion のページでは、実例も含めて解説しています。
更新履歴
- 2022. 2. 5.
- 新規公開。
- 2023. 3.31.
- ページ冒頭に難易度表記を追加。