1.どういう解法?
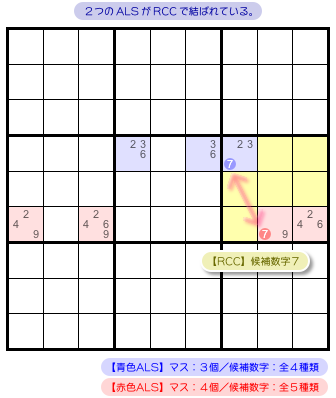
図1-1 を見てみましょう(部分図です)。
青色と赤色、2つの ALS がありますね。
盤面は次の状況になっています。
- 青色 ALS は3マスで、候補数字は2, 3, 6, 7。
- 赤色 ALS は4マスで、候補数字は2, 4, 6, 7, 9。
- 青色⇔赤色 を結ぶ RCC は7。すべて黄色ブロックに属する。
- RCC 以外にも 2つの ALS には共通の候補数字がある。
2つの ALS が1種類の RCC で結ばれているんですね。
あっ。
シレッと4番目に「共通の候補数字がある」なんて書きましたが、これは密かに大事な要素です。
図1-1 で言うと2と6が共通していますね。
これも少し頭の片隅に置いておいてください。
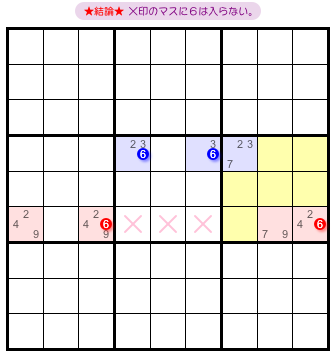
さて、図1-1 からはどういう結論が得られるんでしょう?
こうなるんです。
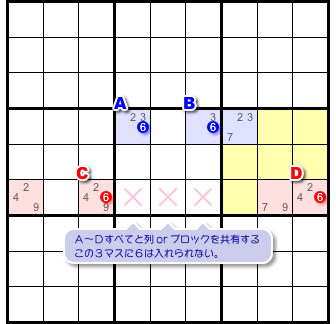
- 2つの ALS が持つすべての候補数字6と列やブロックを共有するマスがある。そのマスに数字6は入らない。
図1-2 だと、×印の3マスが該当します。
この3マスは2マス6と同じブロックに属し、同時に、2マス6と同じヨコ列に属しています。
この3マスに数字6は入らないというわけです。
なぜこういう結論になるんでしょう?
それは、4マス6666のどこかに必ず数字6が入るからなんです。
それを解説しましょう。
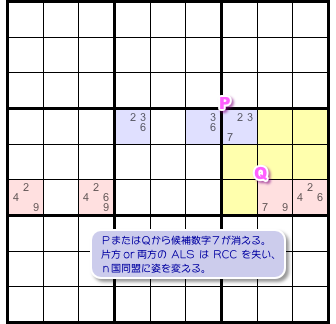
理由は RCC で結ばれた ALS はどうなる? のページでも述べましたが、ここでも述べることにしましょう。
2つの ALS に対してこれが必ず成り立つからなんです。
- 少なくとも一方の ALS はn国同盟に変化する。
それはなぜか?
RCC(候補数字7)はすべて黄色ブロックの中にありますね。
だから、数字7をマスP, Q両方に入れるということはできません。
ということは、少なくともP, Qのどちらかからは候補数字7が消えてしまうわけなんですね。
そうなると、少なくとも青色・赤色 ALS のどちらかは RCC を失うことになります。
その ALS はn国同盟に変化するんですね。
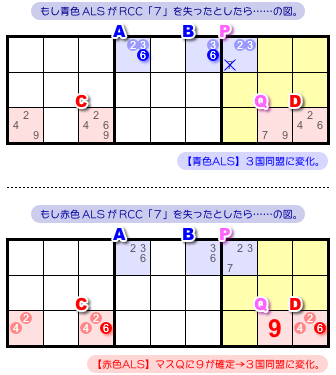
各 ALS が RCC を失った場合の想像図を 図1-4 に示します。
どちらも3国同盟に変化しますね。
青色 ALS は2, 3, 6の3国同盟。
赤色 ALS は2, 4, 6の3国同盟。
さて、ここで2つの ALS に共通する候補数字を見てみましょう。
2と6ですね。
ここでは候補数字6に注目してみます。
青色 ALS が3国同盟になった場合、A, Bのどちらかに数字6が入ることが確定します。
赤色 ALS が3国同盟になった場合、C, Dのどちらかに数字6が入ることが確定します。
よって、「AorBに6が入る」「CorDに6が入る」のうち最低1つは成り立つことになりますね。
これはもうちょいシンプルに言い換えできます。
こんなふうに。
- 4マスA〜Dのうち少なくとも1つに数字6が入る。
そうなると、数字6の入れられないマスが生じます。
×印の3マスです(図1-5)。
実は、この3マスには共通点があるんです。
- 4マスA〜Dと列やブロックを共有している。
×印マスはA, Bと同じブロックに属し、同時に、C, Dと同じヨコ列に属しているんですね。
前図1-4 で説明した通り4マス6666のどこかには必ず数字6が入るのだから、×印の3マスに6を入れることはできない。
こういうわけなんです。
図1-2 の結論通りになりましたね😊
あっ。
そういえば、候補数字2も両方の ALS に存在していましたね。
じゃぁ、2はどうなんでしょう?
6と同じように何か結論は出るのかな……?
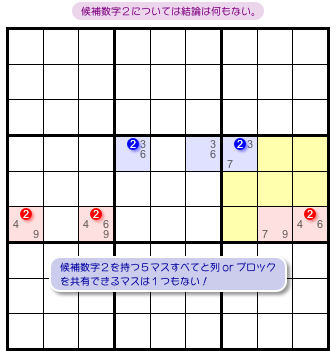
実は、2については何の結論も出ません。
なぜなら、すべての候補数字2と列やブロックを共有できるマスは1つもないからです。
一応、数字2に対しても同じことは言えるんです。
RCC が消えることで青色・赤色 ALS のどちらかはn国同盟に変わるから、5マス22222のどこかには必ず数字2が入る。
しかし、論理展開はここで終わり😞
この5マスすべてと列やブロックを共有できるマスは1つもないため、何の結論も出せないのです。
候補数字の配置によっては、結論が出ないこともある。
せっかく ALS-XZ が使えたのに、ちょい悔しい。
このセクションでは1種類の RCC による解法を解説しました。
実は、RCC が2種類ある場合もあって、これはセクション3で解説しています。
2種類の方の解法は Doubly-Linked ALS-XZ と呼ぶことがありますが、それに対して、1種類の方を Singly-Linked ALS-XZ と呼ぶことがあります。
2.実際に使ってみよう!
ALS-XZ という解法には、前セクションで挙げたもの以外にも多種多様なパターンがあります。
その中から2つ紹介しましょう。
2-1.1マスに作用するパターン
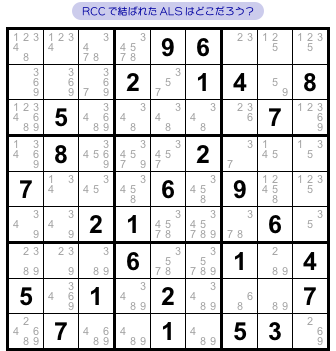
まずは1つめの例。
図2-1 には、ALS-XZ が使える箇所があります。
そのために、まずは RCC で結ばれた2つの ALS を探さなければいけません。
さて、その ALS はどこに潜んでいるでしょう?
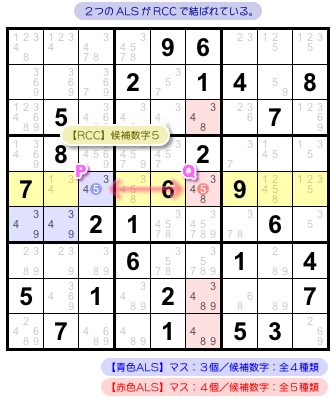
RCC で結ばれた ALS は 図2-2 の通りです。
青色と赤色が ALS です。
こういう状況になっています。
- 青色 ALS は3マスで、候補数字は3, 4, 5, 9。
- 赤色 ALS は4マスで、候補数字は3, 4, 5, 8, 9。
- 青色⇔赤色 を結ぶ RCC は5。すべて黄色ヨコ列に属する。
- RCC 以外にも 2つの ALS には共通の候補数字がある。
RCC のあるマスはPとQ。
2つの ALS が RCC で結ばれていますね。
RCC 以外で共通の候補数字は3, 4, 9といっぱいありますが、ここでは9に注目しておいてください。
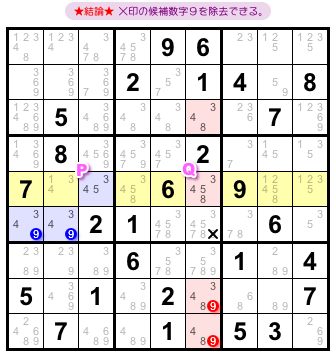
この場合はどういう結論が得られるんでしょう?
こうなります。
- 候補数字9を除去できるマスが1つある。
図2-3、中央ブロックに存在します。×印を付けています。
この1マスから候補数字9を除去できるんです。
なぜ、こういう結論になるんでしょう?
それは、候補数字9を持つ4マス9999のどこかに必ず9が入ることになるからです。
それを解説しましょう。
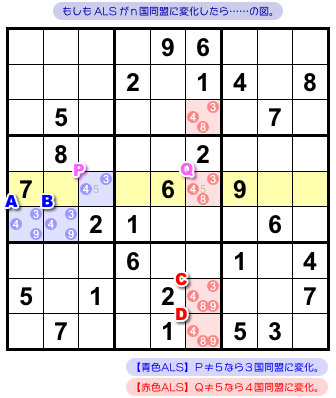
RCC(候補数字5)を持つ2マスP, Qは黄色ヨコ列に属しています。
だから、P, Qの両方に数字5を入れるということができません。
P, Qの少なくとも一方には5は入らないんですね。
PやQに数字5が入らない場合の想像図を 図2-4 に示します。
マスPに5が入らない場合、青色 ALS は3国同盟に変化します。
よって、9はA, Bのどちらかに必ず入ることになる。
マスQに5が入らない場合、赤色 ALS は4国同盟に変化します。
よって、9はC, Dのどちらかに必ず入ることになる。
そのため、最終的にはこういう結果になるんです。
- 4マスA〜Dのうち少なくとも1つに数字9が入る。
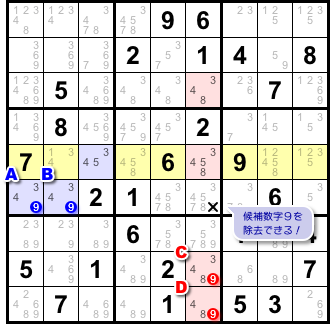
そうなると、候補数字9を除去できるマスが生じます。
×印を付けた1マスです(図2-5)。
この1マスには次の特徴があります。
- 4マスA〜Dとタテ列やヨコ列を共有している。
4マス9999のうち少なくとも1つに数字9が入る。
だから、×印の通り候補数字9を除去できるんです。
図2-3 の結論通りになりましたね😊
ところで。
2つの ALS は候補数字3も4も共通して持っていますね。
3や4についてはどうでしょう?
実は、どちらの場合も結論はありません。
2つの ALS は候補数字3を合計6個持っていますが、それらすべてと列やブロックを共有できるマスは1つもないからなんです。
候補数字4も同様です。
2-2.複数のマスに作用するパターン
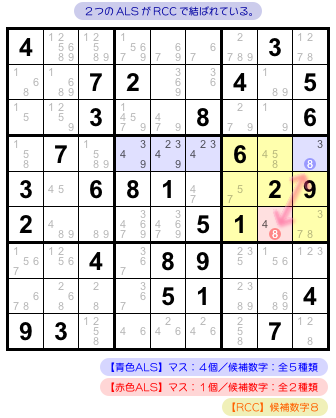
例をもうひとつ。
今度は ALS を最初から示しちゃいます。
確認してみましょう。
こういう状況です。
- 青色 ALS は4マスで、候補数字は2, 3, 4, 8, 9。
- 赤色 ALS は1マスで、候補数字は4, 8。
- 青色⇔赤色 を結ぶ RCC は8。すべて黄色ブロックに属する。
- RCC 以外にも 2つの ALS には共通の候補数字がある。
2つの ALS が RCC で結ばれていますね。
RCC 以外で共通の候補数字は4です。
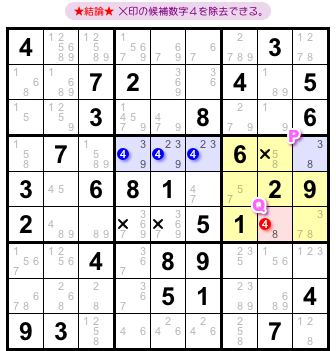
この場合はどういう結論が得られるんでしょう?
こうなります。
- 候補数字4を除去できるマスが3つある。
図2-7、中段あたりに存在します。×印を付けています。
この3マスから候補数字4を除去できるんです。
なぜ、こういう結論になるんでしょう?
それは、候補数字4を持つ4マス4444のどこかに数字4が入ることになるからです。
それを解説しましょう。
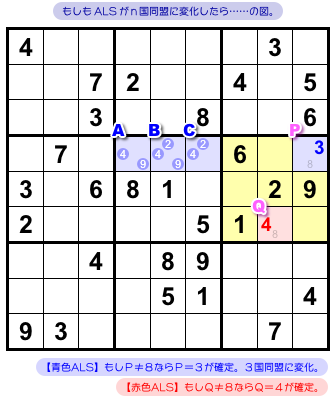
RCC(候補数字8)を持つ2マスP, Qは黄色ブロックに属しています。
だから、P, Qの両方に数字8を入れるということができません。
P, Qの少なくとも一方には8は入らないんですね。
PやQに数字8が入らない場合の想像図を 図2-8 に示します。
マスPに8が入らない場合、Pに数字3が確定したあと青色 ALS は3国同盟に変化します。
マスQに8が入らない場合、赤色 ALS は……なんと、数字4が確定しちゃいます!
というわけで、最終的にはこうなるんですね。
- 4マスA, B, C, Qのうち少なくとも1つに数字4が入る。
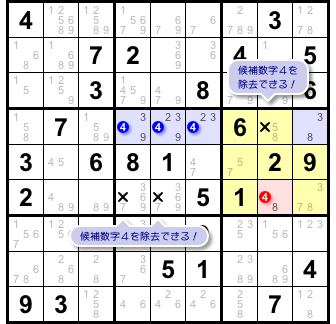
そうなると、候補数字4を除去できるマスが生じます。
×印を付けた3マスです(図2-9)。
この3マスには共通点があります。
- 4マスA, B, C, Qと列やブロックを共有している。
4マス4444のうち少なくとも1つに数字4が入ります。
だから、×印の通り候補数字4を除去できるんです。
図2-7 の結論通りになりましたね😊
ALS-XZ では、少なくとも1つの ALS がn国同盟に変化します。
しかし、どちらの ALS なのかはわかりません。
それどころか、片方なのか両方なのかさえもわからない!
だから、n国同盟になるのがわかっているのにn国同盟の解法を直接使えるわけではありません。
あぁ〜なんとももどかしい😓
そのため、「どっちの ALS がn国同盟になったとしても、少なくともこういうことが成り立つよ〜!」という方向で論理展開していくことになります。
そこで、「両方の ALS に共通する候補数字」に注目するわけですね。
3.Doubly-Linked ALS-XZ もあるよ!
今までは、1種類の RCC で結ばれた ALS についての解法を紹介しました。
このセクションからは、2個の RCC で結ばれた ALS についての解法を紹介しましょう。
3-1.どういう解法?
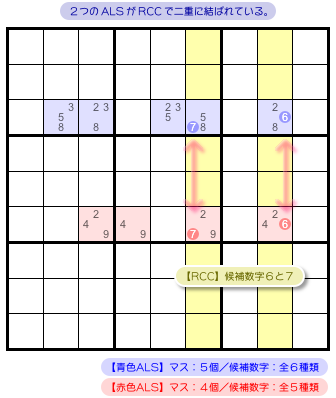
図3-1 を見てみましょう(部分図です)。
青色と赤色が ALS です。
盤面はこういう状況になっています。
- 青色 ALS は5マスで、候補数字は2, 3, 5, 6, 7, 8。
- 赤色 ALS は4マスで、候補数字は2, 4, 6, 7, 9。
- 青色⇔赤色 を結ぶ RCC は6と7。どちらも各タテ列に属している。
2つの ALS が2種類の RCC で二重に結ばれているという状況です。
さて、図3-1 の場合はどういう結論が得られるんだろう?
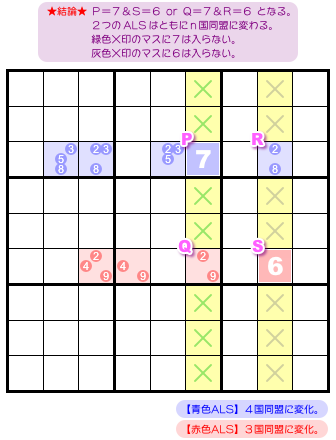
結論はこうなります。
- RCC である6と7が1個ずつ分かれて各 ALS に入り、2つの ALS はともにn国同盟に変化する。
- RCC を共有しているタテ列において、ALS 以外のマスから候補数字 RCC を除去できる。
- 各 ALS に対して、n国同盟の解法が使えるようになる。
a. b. は 2つの RCC で二重に結ばれた ALS もある! で説明した結論と同じものです。
ここでは軽く説明します。
P=7&S=6 または Q=7&R=6 のどちらかが成り立つということです。
2種類の RCC は各 ALS に1個ずつ分かれて入ることになり、どちらの ALS も RCC を1個ずつ失ってn国同盟に変化します。
そして、RCC である7はPとQのどちらかに必ず入ることになるため、緑色×印のマスには数字7は入れられなくなります。同様に、灰色×印のマスには数字6は入りません。
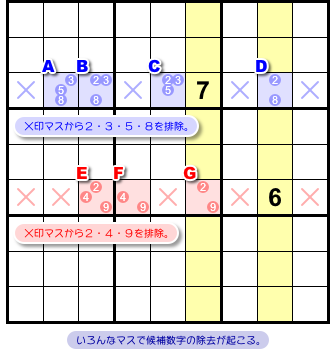
どちらの ALS もn国同盟になることがわかりました。
じゃぁ、今度はn国同盟の解法を使っていきましょう!
ここでは、P=7&S=6 として話を進めていきます。
マスA〜Dの4国同盟はヨコ列上にあります。
そのヨコ列では、A〜D以外のマスに2, 3, 5, 8を入れることはできなくなります(青色×印)。
マスE〜Gの3国同盟もヨコ列上にあります。
そのヨコ列では、E〜G以外のマスに2, 4, 9を入れることはできなくなります(赤色×印)。
ずいぶん多くのマスに作用しましたね!
これが 図3-2 の c. です。
Doubly-Linked ALS-XZ の場合、両方の ALS は必ずn国同盟に変化します。
だから、変化後はn国同盟の解法を直接使えます。
そのため、Singly-Linked ALS-XZ で使った論理展開はまったく必要ありません。
RCC 以外で共通の候補数字があるかどうかを調べなくてもいいんです。
ただし、RCC はどちらかの ALS に必ず入るため、各 RCC の属する列やブロックに影響が出ることを見逃してはいけません。
その列やブロックにおいて、ALS とは無関係なマスに RCC を入れられないのです。
3-2.実際に使ってみよう!
Singly-Linked ALS-XZ と同様、Doubly-Linked ALS-XZ という解法も多様なパターンがあります。
その中から1つ紹介します。
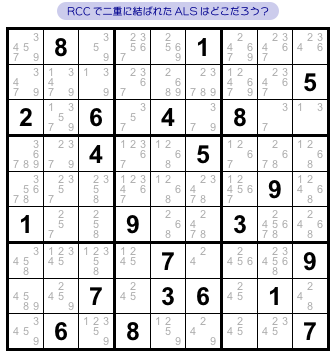
図3-4 には、Doubly-Linked ALS-XZ が使える箇所があります。
RCC で二重に結ばれた2つの ALS が 図3-4 の盤面にはあるわけですが、さて、その ALS はどこに潜んでいるでしょう?
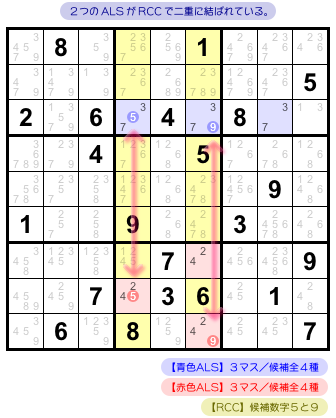
その ALS は 図3-5 の通りです。
確認してみましょう。
こういう状況です。
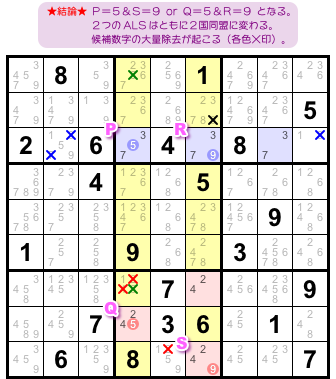
- 青色 ALS は3マスで、候補数字は3, 5, 7, 9。
- 赤色 ALS も3マスで、候補数字は2, 4, 5, 9。
- 青色⇔赤色 を結ぶ RCC は5と9。どちらも各タテ列に属している。
2つの ALS が2種類の RCC で二重に結ばれているという状況です。
この場合はどういう結論が得られるんでしょう?
図3-5 からの具体的な結論はこうなります。
- P=5&S=9 or Q=5&R=9 のどちらかが成り立つ。ALS はともに2国同盟に変化する。
- 左側の黄色タテ列では、すべての黄色マスから候補数字5を除去できる。右側の黄色タテ列では、すべての黄色マスから候補数字9を除去できる。
- 青色 ALS の属するヨコ列では、青色以外のマスから候補数字3と7が除去される。赤色 ALS の属するブロックでは、赤色以外のマスから候補数字2と4が除去される。
図3-6 では、4色の×印で示した9個の候補数字が除去されます。
b. による除去は、緑色×印の5、黒色×印の9です。
c. による除去は、青色×印の3と7、赤色×印の2と4です。
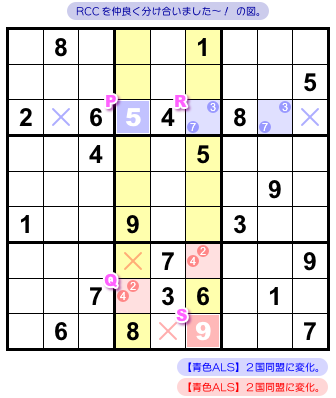
a. b. が成り立つ理由は、2つの RCC で二重に結ばれた ALS もある! で説明した通りです。
2つの ALS の間で RCC(候補数字5と9)を1つずつ分け合うことになり、5も9もどちらかの ALS 内部に入ります。
つまり、P=5&S=9 か Q=5&R=9 か、どちらかが成り立つことになります。
よって、5はマスP, Qのどちらかに必ず入ることになり、左側タテ列では黄色マスに5は入れられません。
9も同様で、右側タテ列ではR, S以外の黄色マスに9は入りません。
c. は2国同盟そのまんまです。
青色2国の属するヨコ列では、国外のすべてのマスから候補数字3と7が除去されます(青色×印)。
赤色2国の属するブロックでは、国外のすべてのマスから候補数字2と4が除去されます(赤色×印)。
以上から、図3-6 の結論が得られることになります。
更新履歴
- 2022. 2. 5.
- 新規公開。
- 2023. 3.31.
- ページ冒頭に難易度表記を追加。