0.まずはn国同盟を軽〜くおさらい
まずは前準備をひとつ。
Naked タイプのn国同盟を軽くおさらいしておきましょう。
Naked なn国同盟とは次のような状態のことでした。
- ある列やブロックに属するn個のマスには全n種類の候補数字がある。
- すると、そのn個のマス達はその全n種類の数字達で占拠されてしまうことになる。
図0-1 を見てみましょう。
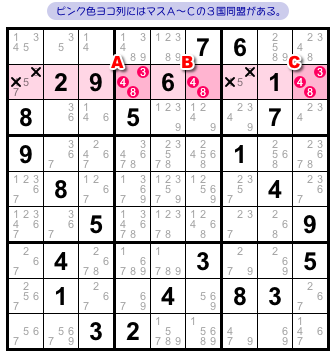
ピンク色ヨコ列の3マスA〜Cは3国同盟(Naked Triple)の状態になっています。
候補数字は3, 4, 8の全3種類ですね。
この場合、数字3, 4, 8はマスA〜Cに固定されますね。
そのため、A〜C以外のピンク色マスから候補3, 4, 8をすべて除去できます(図0-1 ×印)。
これが3国同盟というものでした。
ある列やブロックを見ると、全n種類の候補数字を持つマスがn個ある。
これが Naked タイプのn国同盟なんですね。
「全n種類」の箇所を頭の片隅に置きながら、セクション1をご覧ください。
1.Almost Locked Set (ALS) とは何ぞや?
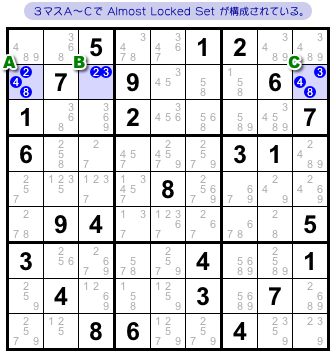
図1-1 を見てみましょう。
上から2番目のヨコ列、マスA〜Cに注目します。
さて、この3マスの候補数字、全部で何種類あるでしょう?
正解は4種類ですね。
2, 3, 4, 8の全4種類。
3マスに対して全4種類ですか。
あら、3国同盟とはちょっと違うんですね。
1種類余分に多いから。
候補数字が1種類余分に多い。
これが大きな特徴なんです。
A〜Cの3マス一組、これが Almost Locked Set です。
一般的な話をしましょう。
ある列やブロックの中に全n種類の候補数字を持つn個のマスがある。これをn国同盟(Naked タイプ)と呼びました。
ある列やブロックの中に全 n+1 種類の候補数字を持つn個のマスがある。これが Almost Locked Set なんです。
「オールモストなんちゃら」と言うと舌がほぼロックされちゃうから、以降は ALS と略しちゃいます。
最も小さい ALS は「全2種類の候補数字を持つ1個のマス」です。
最も大きい ALS は「全9種類の候補数字を持つ8個のマス」です(9×9サイズの場合)。
図1-1 では、3マスA〜Cは同じヨコ列にありました。
実は、これは重要です。
ALS を構成するマスはすべて同じ列または同じブロックに属していなければいけません。
ただただ適当にマスを集めて「これが ALS だ〜!」と言うわけにはいきません。
注意しましょう。
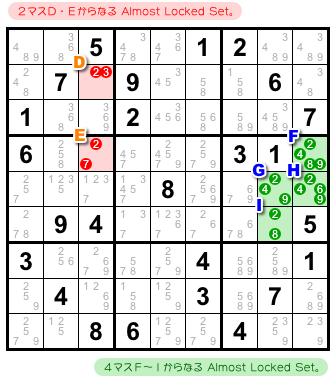
前図1-1 の盤面には、他にも ALS が存在します。
図1-2 で例を2つ挙げてみます。
まずは、左から3番目のタテ列。
2マスD, Eを見ると、候補数字は2, 3, 7の全3種類。
2マスからなる ALS ですね。
次に中央右ブロック。
4マスF〜Iを見ると、候補数字は2, 4, 6, 8, 9の全5種類。
4マスからなる ALS です。
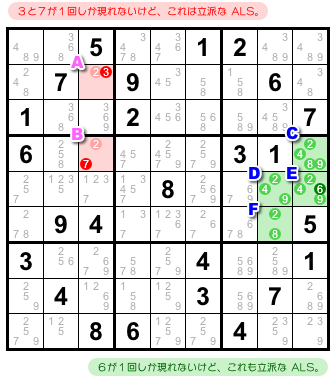
ある候補数字が ALS 内部では1回しか現れない、ということがあります。
そういう候補数字があってもOKです。
例えば、図1-3 の赤色 ALS では、候補数字3はマスAにしかなく、候補数字7はマスBにしかありません。
それでもOKです。正当な ALS です。
図1-3 の緑色 ALS では候補数字6はマスEにしかありません。
もちろん、これも正当な ALS です。
2.これが ALS の重要な特徴だ!
セクション1では ALS を定義しましたが、それだけではまだ足りません。
ALS の解法を理解するにあたって、とある特徴を知っておかなければいけないんです。
それはどういう特徴なんだろう?
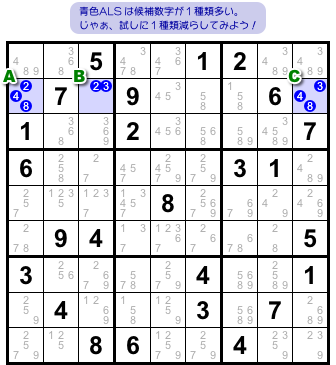
図2-1 のように、ALS は全 n+1 種類の候補数字を持っています。
マスの個数より1多い。
こういう性質があるんでしたね。
では、ここで疑問を1つ投げてみましょう。
もし ALS から1種類の候補数字が消えたとしたら、果たしてどうなりますか?
つまり、全 n+1 種類から1減って全n種類になったとしたら……?
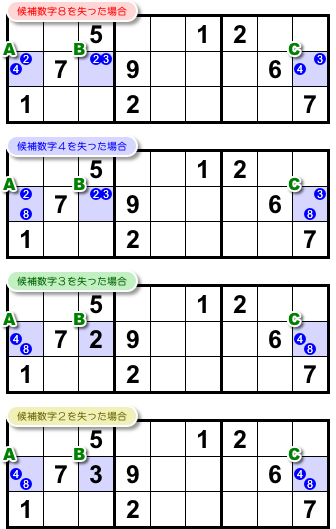
ALS はこうなるんです。
- ALS から1種類の候補数字が消えると、その ALS はn国同盟に変化する。
これが ALS の重要な特徴なんです。
前図2-1 の ALS から候補数字を1種類失ったらどうなるか。
4通り全部試してみましょう。
候補数字8を失った場合は、2, 3, 4の3国同盟に変わります。
候補数字4を失った場合は、2, 3, 8の3国同盟に変わります。
候補数字3を失った場合は、マスBに2が確定し、2マスA, Cの2国同盟に変わります。
候補数字2を失った場合は、マスBに3が確定し、2マスA, Cの2国同盟に変わります。
4通りを 図2-2 に示しましたが、どれもn国同盟に変わってもぅた!
まさに "Almost" Locked Set ですね!
何かがキッカケとなって候補数字を1種類失うと、その ALS はたちまちn国同盟(Locked Set)に姿を変えてしまうんです。
ALS を使った解法では、この「ALS が候補数字を1種類失う」という過程がキーになります。
だから、ALS 系の解法を理解する時は、このセクションの内容を必ず理解しておきましょう。
3.Restricted Common Candidate (RCC) とは何ぞや?
次は、Restricted Common Candidate の説明です。
これはとある候補数字のことを指し、2つの ALS を結ぶといった役割を持っています。
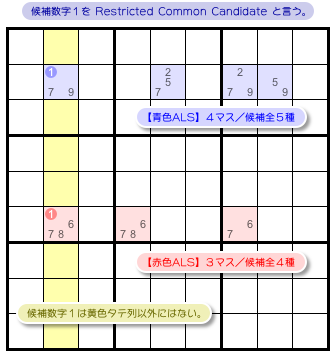
図3-1 を見てみましょう(部分図です)。
上から2つめのヨコ列を見ると青色4マスの ALS があります。候補数字は1, 2, 5, 7, 9の全5種類。
そして、下から4つめのヨコ列を見ると赤色3マスの ALS があります。候補数字は1, 6, 7, 8の全4種類。
この2つの ALS には次の特徴があります。
- 2つの ALS には共通の候補数字1がある。
- その候補数字1はすべて黄色タテ列に属している。
- どちらの ALS も、候補数字1はその黄色タテ列以外には存在していない。
まるで、2つの ALS を候補数字1が結んでいるような形ですね。
この候補数字1が Restricted Common Candidate です。
一般的な話をしましょう。
2つの ALS が次の条件を満たしていたとします。
- 2つの ALS には共通の候補数字aがある。
- 候補数字aはすべて同じ列X(または同じブロックX)に属している。
- どちらの ALS も、候補数字aはX以外には存在していない。
この時、候補数字aを Restricted Common Candidate と呼びます。
「リストリクテッドコモンキャンディデーなんちゃら」なんて舌を噛むんで、以下では RCC と略しちゃいます。
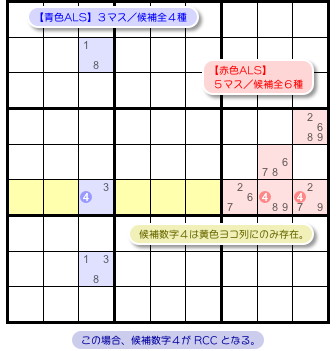
もう一例を示しましょう。
図3-2 です。
タテ列の中に青色 ALS、ブロックの中に赤色 ALS があります。
- 青色 ALS は3マスで、候補数字は1, 3, 4, 8。
- 赤色 ALS は5マスで、候補数字は2, 4, 6, 7, 8, 9。
候補数字4に注目しながら以下の特徴を確認してみてください。
- 2つの ALS には共通の候補数字4がある。
- その候補数字4はすべて黄色ヨコ列に属している。
- どちらの ALS も、候補数字4はその黄色ヨコ列以外には存在していない。
候補数字4が RCC です。
RCC は1個ずつ存在するとは限らないので、注意しましょう!
例をもう1つだけ。
例ばっかりでホントすいませ〜ん😅
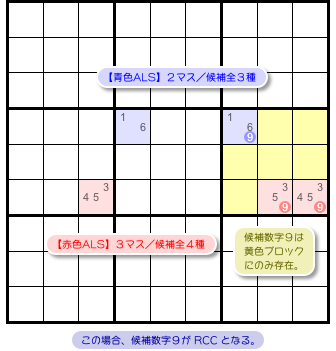
図3-3 を見てみましょう。
青色と赤色が ALS です。
- 青色 ALS は2マスで、候補数字は1, 6, 9。
- 赤色 ALS は3マスで、候補数字は3, 4, 5, 9。
この2つの ALS には以下の特徴があります。
候補数字9に注目しながら確認してみてください。
- 2つの ALS には共通の候補数字9がある。
- その候補数字9はすべて黄色ブロックに属している。
- どちらの ALS も、候補数字9は黄色ブロック以外には存在していない。
候補数字9が RCC です。
ALS を使った解法では、この「ALS が RCC でつながっている」という状況がキーになります。
だから、ALS 系の解法を理解する時は、セクション2とともにこのセクションの内容を必ず理解しておきましょう。
4.RCC で結ばれた ALS はどうなる?
これまで ALS と RCC について説明しました。
でも、この2つは一体どう役立つんでしょう?
このセクションでは、RCC で結ばれた2つの ALS から何が言えるのかを解説していきます。
セクション2の内容も関わってくるので、それを思い出しておきましょう。
実は、RCC で結ばれた2つの ALS に対して、こういう結論が待っているんです。
- RCC で結ばれた2つの ALS のうち、少なくとも一方は必ず RCC を失ってn国同盟に変化する。
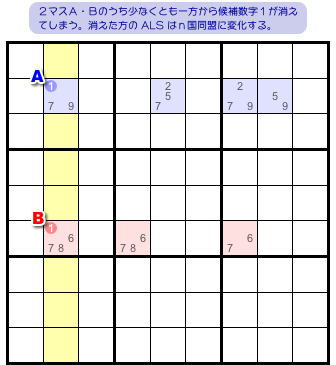
図3-1 の ALS を使って説明しましょう。
今、RCC(候補数字1)を持つマスA, Bに注目します。
AとBは同じタテ列に属していますね。だから、両方に数字1を入れるということはできません。
つまり、A, Bの少なくとも一方に数字1は入りません。
数字1が入らないということは、ALS から候補数字1が消えるということと同じ。
というわけで、こうなるんです。
- 少なくとも一方の ALS は RCC(候補数字1)を失う。
その ALS はn国同盟に姿を変える。
なんと!
セクション2で説明したことが起こるんです。
もぅちょっと詳しく説明しましょう。
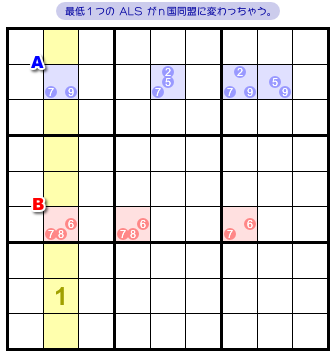
現状、黄色タテ列のどこに数字1が入るかはわかりません。
だけど、黄色列のどこに数字1が入ろうとも、片方or両方の ALS は必ずn国同盟に変化するんです。
例えば、マスAに1が入ると、マスBは候補数字1を失う。赤色 ALS は3国同盟(6, 7, 8)に変化する。
マスBに1が入ると、マスAは候補数字1を失う。青色 ALS は4国同盟(2, 5, 7, 9)に変化する。
黄色マスに1が入ると、図4-2 のように ALS は両方ともn国同盟になっちゃう!
こういうことが起こるんです。
今はまだ RCC のおかげで2人とも ALS でいられる。
しかし、1人は必ずn国同盟へと姿を変えなければならない。
これは、RCC で結ばれた ALS 達の宿命です。
前図4-1 で述べた結論は、主に ALS-XZ という解法で使われます。
詳細は ALS-XZ のページをご覧ください。
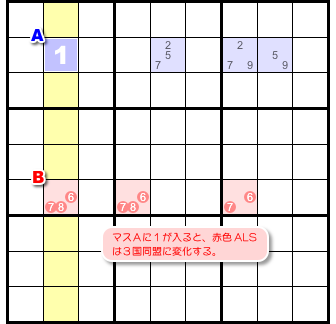
もうひとつ、簡単な結論を紹介しましょう。
- 2つの ALS の一方に RCC が入った場合、他方は必ずn国同盟に変化する。
これはもぅ簡単です。
もしマスAに数字1が入ったら、赤色 ALS は3国同盟に変化する。
もしマスBに数字1が入ったら、青色 ALS は4国同盟に変化する。
こういうことですね。
図4-3 は前者の場合を表しています。
この結論は、主に ALS-XY-Wing や ALS-XY-Chain という解法の中で使われます。
詳細は ALS-XY-Wing、ALS-XY-Chain のページをご覧ください。
1種類の RCC を使った解法は Singly-Linked を冠した名前で呼ぶことがあります。
例えば、ALS-XZ のページで解説している解法は、Singly-Linked ALS-XZ とも呼びます。
5.2種類の RCC で二重に結ばれた ALS もある!
セクション4では、1種類の RCC で結ばれた ALS を紹介しました。
実は、2種類の RCC で ALS が二重に結ばれる場合もあるんです。
このセクションでは、そういう ALS を解説します。
5-1.概要
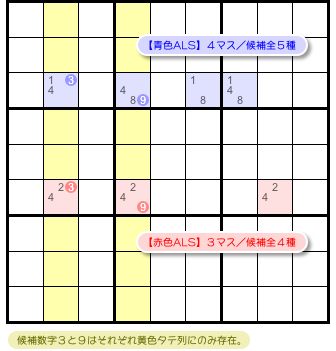
図5-1 を見てみましょう(部分図です)。
青色と赤色の ALS がありますね。
この2つの ALS には次の特徴があります。
- 2つの ALS には共通の候補数字3がある。
- 候補数字3はすべて左側の黄色タテ列に属している。
- どちらの ALS も、候補数字3はその黄色タテ列以外には存在していない。
そして、もうひとつ特徴があります。
- 2つの ALS には共通の候補数字9がある。
- 候補数字9はすべて右側の黄色タテ列に属している。
- どちらの ALS も、候補数字9はその黄色タテ列以外には存在していない。
なんと、同じ性質を持つ候補数字が2種類もある!
この候補数字3と9が RCC です。
ALS は RCC で二重に結ばれているんですね。
一般的な話をしましょう。
2つの ALS が次の条件を満たしているとします。
- 2つの ALS には共通の候補数字aとbがある。
- 候補数字aはすべて同じ列X(または同じブロックX)に属している。
- 候補数字bはすべて同じ列Y(または同じブロックY)に属している。
- どちらの ALS も、候補数字aはX以外には存在していない。
- どちらの ALS も、候補数字bはY以外には存在していない。
なんだか多くてホントすいませ~ん😅
図5-1 でビジュアル的に理解しちゃってください。
上記の条件を満たす時、候補数字aとbを RCC と呼びます。
2種類の RCC を使った解法は Doubly-Linked を冠した名前で呼ぶことがあります。
例えば、Doubly-Linked ALS-XZ などの解法があります。
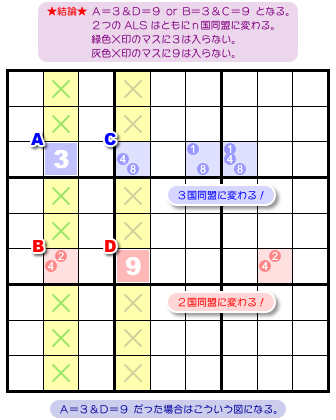
さて、二重に結ばれた ALS からはどういう結論が得られるんでしょう?
こうなるんです。
- 2種類の RCC が1つずつ分かれて各 ALS に入り、2つの ALS はともにn国同盟に変化する。
- 各 RCC の属する列またはブロックにおいて、ALS 以外のマスから候補数字 RCC を除去できる。
前図5-1 の ALS で具体的に説明しましょう。
a. は次の通りです。
A=3&D=9 または B=3&C=9 のどちらかが成り立ち、青色 ALS は3国同盟に変化、赤色 ALS は2国同盟に変化するということです。図5-2 は A=3&D=9 の場合を表しています。
b. は次の通りです。
RCC である候補数字3は黄色タテ列の中にありますが、このタテ列では数字3はマスA, Bのどちらかに必ず入り、緑色×印のマスには入らないということです。
もうひとつの RCC も同様です。候補数字9の入る場所はマスC, Dの2カ所に限定され、灰色×印のマスに数字9は入りません。
なんと、セクション4とは結論が全く違うじゃぁないですか!
なぜこういう結論になるんだろう?
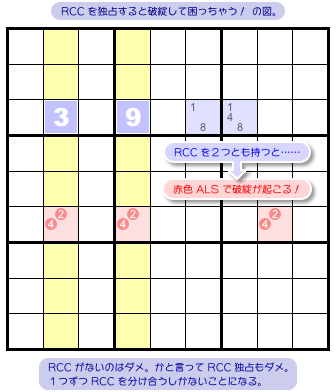
なぜ2つの RCC は各 ALS に1つずつ分かれて入るのか?
まずはそれを説明しましょう。
ALS は「全 n+1 種類の候補数字を持つn個のマス」のことでした。
そこから RCC を2つ失うと「全 n-1 種類の候補数字を持つn個のマス」に変化するわけですね。
実は……、この時点で破綻なんです。
マスはn個あるのに候補数字は全 n-1 種類しかない。これでは数字が足りないんです。図5-3 の赤色3マスのような状態です。
全 n-1 種類の候補数字を n-1 個のマスに入れられるけど、そのあとn個目のマスに入れる数字がもぅない😵
ALS が RCC を2つとも失うと破綻を引き起こすわけですね。
となると、一方の ALS が RCC を独り占めすることもできなくなります。なぜなら、他方の ALS が RCC を2つとも失ってしまうから。
ALS が RCC を2つとも失ったらダメ。
ALS が RCC を2つとも独り占めしてもダメ。
ということは、ALS は RCC を1つだけ持たなければいけません。
結局、ALS の間で RCC を仲良く1つずつ分け合うしかないのです。
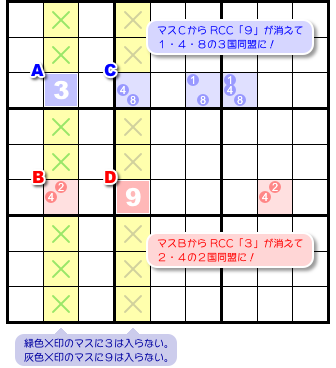
一方の ALS が RCC を持つということは、逆に言えば、他方の ALS はその RCC を失うということでもあります。
つまり、2つの ALS は RCC を1つずつ失って、どちらもn国同盟に変化するというわけなんです。
これが 図5-2 の結論 a. です😊
また、2つの ALS が RCC を分け持つのだから、各 RCC はどちらかの ALS に必ず属することになります。
つまり、数字3はマスA, Bのどちらかに必ず入るし、数字9はマスC, Dのどちらかに必ず入ることが約束されるんですね。
よって、緑色×印マスに3は入れられず、灰色×印マスに9は入れられないんです(図5-4)。
これが 図5-2 の結論 b. です😊
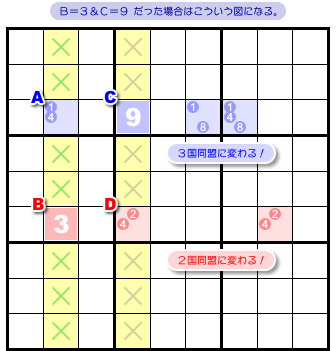
図5-2 では A=3&D=9 の場合を示しましたが、B=3&C=9 の場合も図で表してみましょう。
青色 ALS は3国同盟になりました。
赤色 ALS は2国同盟になりました。
この場合も、両方の ALS はn国同盟に変化しましたね。
RCC の入り方は一意ではないものの、どちらの ALS も必ずn国同盟に変わるんですね。
もちろん、黄色2列がバツだらけになることも変わりません。
セクション4のタイプとはまったく異なる結果になっていることに注意しましょう!
2つの RCC は必ず ALS に入るから、青色 ALS も赤色 ALS も必ずn国同盟になるわけですね。
だから、n国同盟の解法を直接使うことができます。
5-2.少し複雑なパターン
もうひとつ例を挙げましょう。
今度はちょっと複雑です。
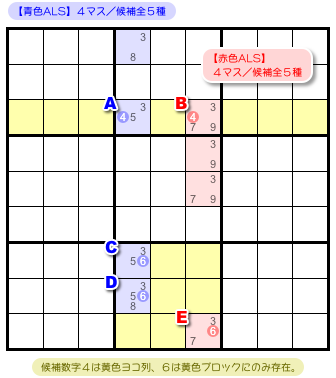
図5-6 を見てみましょう(部分図です)。
図5-6 の2つの ALS には次の特徴があります。
- 2つの ALS には共通の候補数字4がある。
- 候補数字4はすべて黄色ヨコ列に属している。
- どちらの ALS も、候補数字4はその黄色ヨコ列以外には存在していない。
- 2つの ALS には共通の候補数字6がある。
- 候補数字6はすべて黄色ブロックに属している。
- どちらの ALS も、候補数字6はその黄色ブロック以外には存在していない。
この2つの候補数字4と6が RCC です。
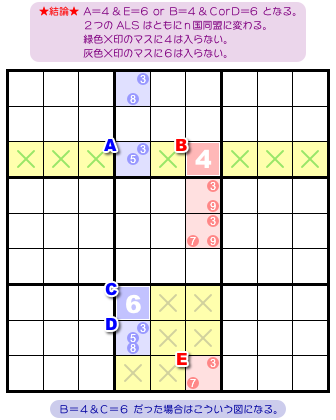
図5-6 からは何が得られるんでしょう?
図5-2 の a. b. と同様の結論が得られますが、具体的には次の通りです。
- 「A=4&E=6」「B=4&CorD=6」のどちらかが成り立ち、2つの ALS はともにn国同盟に変化する。
- 2マスA, Bの属するヨコ列では、A, B以外のマスから候補数字4を除去できる。3マスC〜Eの属するブロックでは、C〜E以外のマスから候補数字6を除去できる。
a. はちょっとややこしい!
後者の組み合わせだと数字6が一意に定まりません。
CorD=6 ですもんね。
しかし、C=6とD=6のどちらであったとしても、青色 ALS はn国同盟に変化します。例えばC=6の場合は 図5-7 のようになります。
b. は 図5-2 と同じです。
2つの ALS は RCC を分け持つため、数字4はマスA, Bのどちらかに必ず入り、数字6はマスC, D, Eのどれかに必ず入ります。
よって、緑色×印マスに4は入れられず、灰色×印マスに6は入れられないことになります(図5-7)。
理由は 図5-3〜図5-4 で説明したことと同じです。
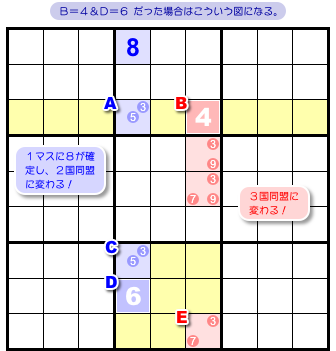
図5-7 ではC=6の場合を示しましたが、D=6の場合も図で表してみましょう。
青色 ALS は最上段の青色マスに8が確定し、2国同盟になりました。
赤色 ALS は 図5-7 と同じで、3国同盟になりました。
この場合も、両方の ALS はn国同盟に変化するんですね。
C=6でもD=6でも、結局、ALS はn国同盟になることが約束されているんです。
更新履歴
- 2022. 2. 5.
- 新規公開。
- 2023. 3.31.
- ページ冒頭に難易度表記を追加。