なぜカバーセットに数字Ｘが入らないの？《Franken Swordfish編・その２》

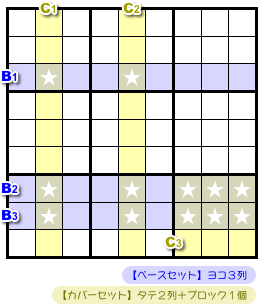
　図1-1 の盤面を例にとりましょう。
　まずは、ベースセットとカバーセットのおさらいをしておきます。

• 青色ヨコ３列において、数字Ｘは★の位置にしか入らない。
• そして、その★マスすべてを３個の黄色 house で覆い尽くせた！

　こういう状況で話を進めていきます。

　ベースセットは青色ヨコ３列で構成されています。
　B₁B₂B₃と名前をつけておきます。
　そして、それぞれを ベース要素 と呼ぶことにしましょう。

　カバーセットは３個の黄色 house で構成されています。
　C₁C₂C₃としておきます。
　そして、それぞれを カバー要素 と呼ぶことにしましょう。

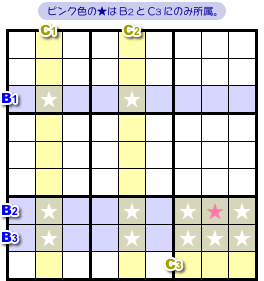
　さて、実はすべての★マスに共通する特徴があります。
　それは、次の特徴です。

• どの★マスも、ただ１つのベース要素とただ１つのカバー要素に属している。

　つまり、どの★マスも複数の青色ヨコ列に所属しておらず、かつ、複数の黄色 house にも所属していません。掛け持ちしていないんですね。
　例えば、図1-2 のピンク色★マスはB₂とC₃にのみ所属しています。

　この「ただ１つの」というのが重要です。

　では、３つのベース要素（青色ヨコ列）に数字Ｘを１個ずつ入れていきます。
　B₁から順に数字Ｘを入れていきましょう。

　もちろん、「どのベース要素も数字Ｘは★マスにしか入らない」という前提を忘れてはいけません。
　だから、どれかの★マスに数字Ｘを入れることになりますね。
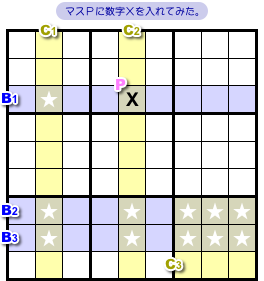
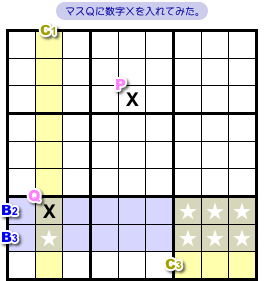
　まず、B₁ではマスＰに数字Ｘを入れてみます（図1-3）。

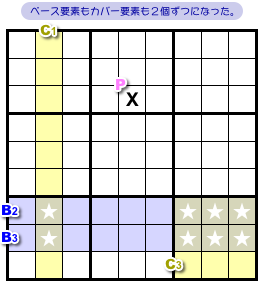
　図1-2 で説明した通り、マスＰの所属するカバー要素は１つだけです。
　C₂だけですね。
　マスＰに数字Ｘが入ったことで、次のようになりました。

• C₂では、★以外の黄色マスに数字Ｘは入らなかった。

　３つのベース要素に数字Ｘを１個ずつ入れるということをやっているので、数字Ｘの入ったB₁はもぅお役御免！
　ということで、除去しちゃいましょう。
　そして、もう数字Ｘの入れられない★とC₂も除去しちゃいます。
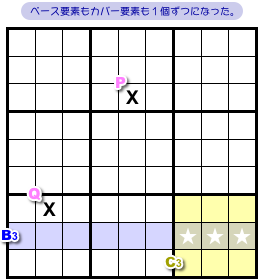
　ベース要素もカバー要素も２個ずつになりました。

　続いて、またベース要素に数字Ｘを入れます。
　次はB₂のマスＱに数字Ｘを入れてみましょう（図1-5）。

　マスＱの所属するカバー要素も１つだけです。
　C₁だけですね。
　マスＱに数字Ｘが入ったことで、次のようになりました。

• C₁では、★以外の黄色マスに数字Ｘは入らなかった。

　数字Ｘの入ったB₂はここでお役御免！
　ということで、除去しちゃいましょう。
　そして、もう数字Ｘの入れられない★マスとC₁も除去しちゃいます。
　ベース要素もカバー要素も１個ずつになりました。

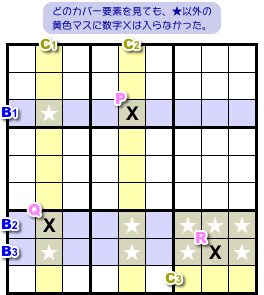
　最後はB₃に数字Ｘを入れるだけ。
　★が３個しか残ってないので、そのどれかに数字Ｘを入れて終わり！
　マスＲにしときましょうか。
　そのマスに数字Ｘを入れたら最後はこうなります。

• C₃では、★以外の黄色マスに数字Ｘは入らなかった。

　さぁ、これですべてのベース要素に数字Ｘを入れ終わりました。
　ここで、カバーセットについてどんなことが成り立ったでしょう？
　順番に全部書いてみます。

• C₂では、★以外の黄色マスに数字Ｘは入らなかった。
• C₁では、★以外の黄色マスに数字Ｘは入らなかった。
• C₃では、★以外の黄色マスに数字Ｘは入らなかった。

　なんと！
　どのカバー要素も、★以外の黄色マスに数字Ｘは１つも入らなかったのです！