1.数字Xの入れ方・全パターン
まず、用語を1つ紹介します。
タテ列・ヨコ列・ブロックをひっくるめた総称があります。それを house と言います。
これは英語のナンプレ解説サイトでも使われている用語で、英語の解説を読むと house というワードがやたらと現れます。
以降は、house という用語を使うことにします。
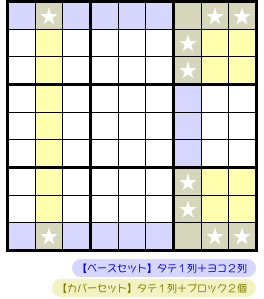
3個の青色 house(ヨコ2列&タテ1列)において、★マスにしか数字Xが入らないとします。
そして、★マスはすべて3個の黄色 house(タテ1列&ブロック2個)に存在しています。
いわば、★マスは3個の黄色 house で完全に覆い尽くされているという状況です。
この時、ベースセットとカバーセットはこうなります。
- ベースセット は3個の青色 house(ヨコ2列&タテ1列)。
- カバーセット は3個の黄色 house(タテ1列&ブロック2個)。
ここで、カバーセットのことは一旦忘れて、ベースセットを構成する青色 house それぞれに試しに数字Xを入れてみます。
さて、数字Xの入れ方は全部で何通りあるでしょう?
もちろん、★以外の青色マスに数字Xを入れてはいけません。
そして、同じ列やブロックに数字Xを2個以上入れてもいけません。
それに注意しながら、何通りあるのかを探っていきましょう。
数字Xの入れ方は全部で8通りあります。
以下の通りです。
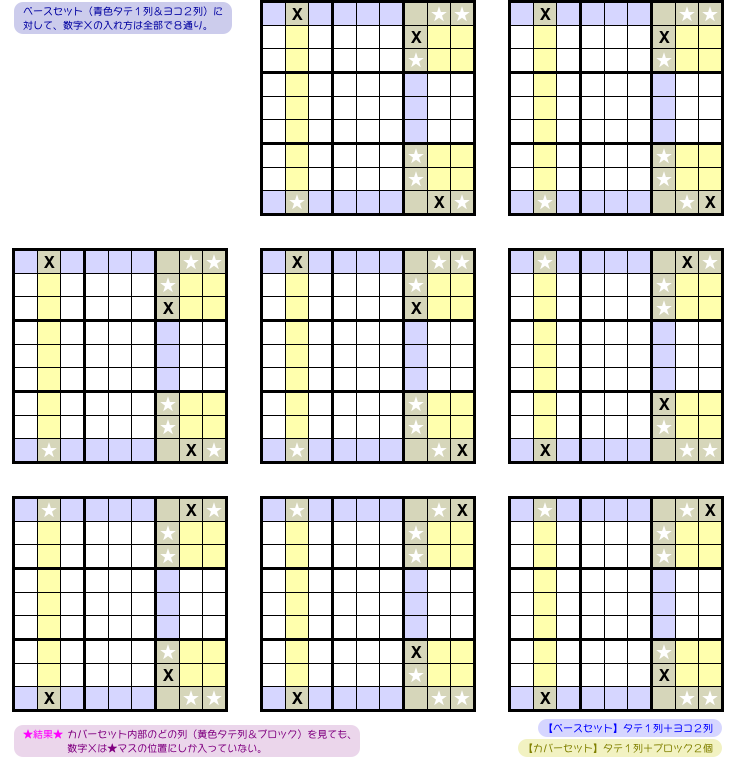
実は、この8通りのパターンには大きな共通点が1つあるんです。
- カバーセット内部のどの house(黄色タテ列&ブロック)を見ても、数字Xは★マスの位置にしか入っていない。
元々、★以外の黄色マスに数字Xが入るか否かは問いませんでした。
しかし、この全8通りの結果によって、黄色マスに数字Xの入る可能性はなくなるんですね。
よって、ベースセットとカバーセットを見つけた時、次の結論が得られます。
- カバーセットを構成するマスのうち、ベースセットに所属していないものがある。
そのマスすべてに数字Xを入れられなくなる(そのマスから候補数字Xを除去できる)。
このページでは全パターンを列挙してこの結論を導きましたが、背理法で導く方法もあります。
つまり、「★以外の黄色マスに数字Xが入ると仮定したら不合理が生じてしまう」という方法です。
実際、どれかの黄色マスに試しに数字Xを入れてみると、ベースセット内部のどこかの列やブロックで「数字Xの入るマスが1つもなくなっちゃった〜!」という破綻が起こります。
2.全パターンの見つけかた
セクション1で「全部で8通りで〜す😊」とか言ってパターンだけ示しましたが、「どうやって8パターン見つけたの?」と疑問に思った方々がいるかもしれません。
その方々に向けてちょいと解説してみます。
しょーもない解説なんで、テキトーに流し読みしちゃってくださ〜い😅
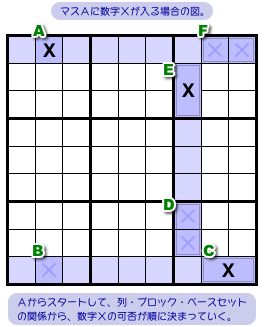
マスAに数字Xが入るか否かで分けて考えましょう。
まずは、マスAに数字Xが入る場合です。
この場合は、マスAから反時計回りに流れを追っていくとわかりやすいです。
具体的には以下の手順で進めます。
- マスAに数字Xが入る。
- Aを含むタテ列では、マスBにXは入らなくなる。
- Bを含む青色ヨコ列では、2マスCのどちらかにXが入ることになる。
- 右下ブロックでは、2マスDにXは入らなくなる。
- Dを含む青色タテ列では、2マスEのどちらかにXが入ることになる。
- 右上ブロックでは、2マスFにXは入らなくなる。
Xの場所について、Cは2通り、Eも2通りに分かれます。
だから、2×2=4 で4通りあります。
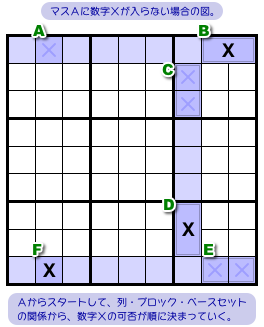
次は、マスAに数字Xが入らない場合です。
この場合は、図2-1 とは逆に時計回りに流れを追っていきます。
具体的には以下の手順で進めます。
- マスAに数字Xは入らない。
- Aを含む青色ヨコ列では、2マスBのどちらかにXが入ることになる。
- 右上ブロックでは、2マスCにXは入らなくなる。
- Cを含む青色タテ列では、2マスDのどちらかにXが入ることになる。
- 右下ブロックでは、2マスEにXは入らなくなる。
- Eを含む青色ヨコ列では、マスFにXが入ることになる。
Xの場所について、Bは2通り、Dも2通りに分かれます。
だから、2×2=4 で4通りあります。
図2-1 と合わせると、8通りあるんですね。