【解法】Broken Wing

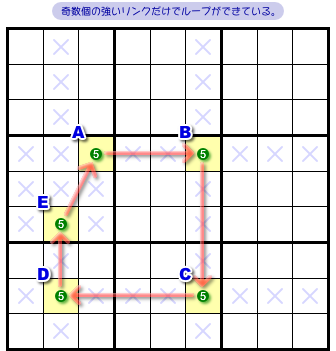
　図1-1 を見てみましょう。
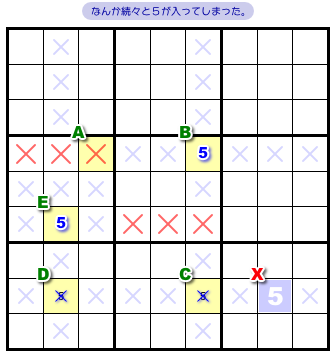
　これは、５以外の候補数字を無視した部分図です。
　この図以降、薄青色の×印を付けたマスに候補数字５は存在しないものと考えてください。

　さて、５マスＡ〜Ｅに注目しましょう。
　この５マス同士が強いリンクで順に結ばれ、強いリンクだけでぐるっと１周していますね。
　一瞥しただけでは、何の変哲もない普通のループのように見えます。

　ところが！
　このループはとんでもない特徴を持っているんです。

• 奇数個の強いリンクでループになっている。

　「とんでもない特徴」だなんて、んな大げさな😅
　いやいやいや、実は、大げさではなかったりします。

　「特徴」を通り越して、致命的な欠陥なんです。

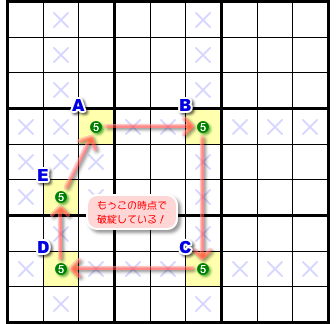
　「致命的な欠陥」だなんて、さらに輪をかけて大げさな😅
　一体、どこら辺が致命的なんでしょう？
　奇数個の強いリンクで１周してる。ただそれだけなんですが……。

　実は……これが致命的な欠陥なんです。

• 「奇数個」のせいで、既に破綻が起きている。

　奇数個。
　これがそもそもの元凶なんです。

　実は、このループ、マスＡに数字５が入っても入らなくても破綻を引き起こしてしまいます。

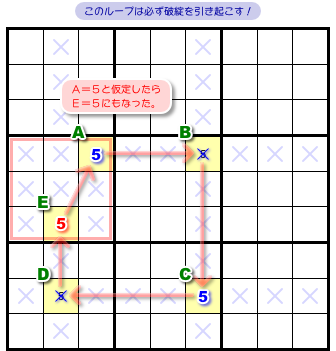
　例えば、「マスＡに数字５が入る」と仮定してみましょう。
　すると、こういう流れが起きます。

1. （仮定）マスＡに５が入る。
2. すると、弱いリンク によりマスＢに５は入らない。
3. すると、強いリンク によりマスＣに５が入る。
4. すると、弱いリンク によりマスＤに５は入らない。
5. すると、強いリンク によりマスＥに５が入る。

　ありゃ？
　ループを１周したら赤枠ブロックに数字５が２個も入ってもぅた。
　これは破綻です😵（図1-3）

　逆に、「マスＡに数字５は入らない」と仮定すると、今度は赤枠ブロックに数字５を１つも入れられなくなってしまう。これも破綻。
　マスＡに数字５が入ろうが入るまいが、破綻にたどり着くんですね。

　あぁ……こりゃ詰みだ🥺

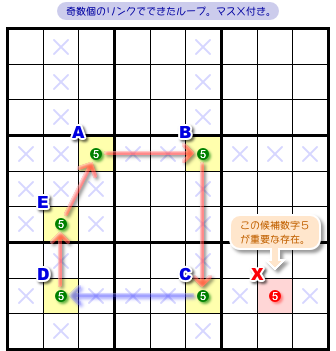
　図2-1 を見てみましょう（部分図です）。
　前セクションの盤面にマスＸを付け足した物です。
　薄青色×印のマスに候補数字５はないものとして、５マスＡ〜Ｅの候補数字５を順にリンクで結んでループができていますね。

　このループ、４個は強いリンクです。
　だけど、１個だけは弱いリンクですね。
　なぜ弱いリンクなのかと言うと、３マスＣ, Ｄ, Ｘに候補数字５があるからです。

• 奇数個のリンクでループができている。
• ループに関わる形でループ外にマス（マスＸのこと）がある。

　ここで、前セクションの話を思い出しましょう。
　図2-1 の状況では、「２マスＣ, Ｄが強いリンクで結ばれる」なんてことが起きてはいけないのです。
　是が非でもそれを阻止しなければならぬ！
　悲劇が起きてはならぬ！

　となると、ある１マスがクローズアップされてくる。
　このループの運命を握る、重要な存在。
　それはマスＸなんです。

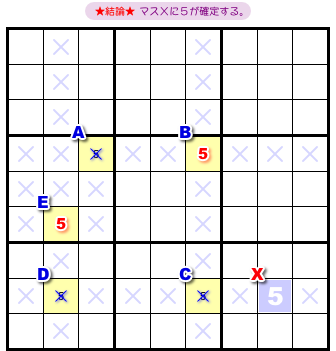
　では、結論です。
　図2-1 からはどうなるのか。

• マスＸに数字５が確定する。

　図2-2 の通りになります。
　重要な存在と言ったマスＸにあっさりと数字が確定してもぅた😊

　なぜ確定するんでしょう？
　それは、マスＸに数字５を入れなければ破綻を引き起こすからです。

　マスＸから候補数字５を除去してしまうと、２マスＣ, Ｄは強いリンクで結ばれてしまう。
　悲劇のループができあがってしまうのです。
　だから、マスＸに５を入れて破綻を回避するしかありません。

　図3-1 では、とあるマスに数字が確定します。
　それを解法 Broken Wing で突き止めてみます。

　この解法を使うためには、奇数個のリンクからなるループを見つけなければいけません。
　そして、破綻を阻止する guardian も必要です。
　それらをを探しましょう！

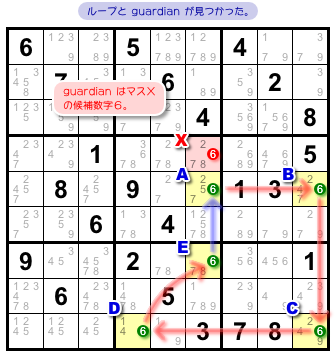
　候補数字６に注目すると見つかりました。
　該当のループと guardian は 図3-2 の通りです。

• 奇数個のリンクでループができている。
• guardian はマスＸの候補数字６。

　まさに Broken Wing の使える形をしていますね！
　早速使いましょう！

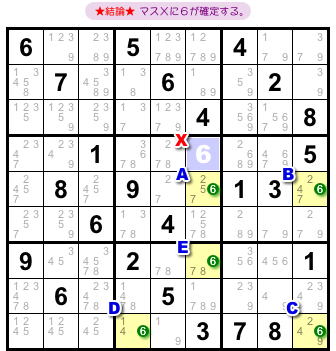
　前セクションと同じ理屈を適用しましょう。
　結論はこうなります。

• マスＸに数字６が確定する。

　guardian のあるマスに数字が確定です！
　guardian が見事に働いてくれました。

　理由は、もちろん、破綻を引き起こさないようにするためです。
　もしマスＸに６が入らないとすると、２マスＡ, Ｅが強いリンクで結ばれてしまう。

　そんな悲劇を招いてはならない。
　だから、マスＸに数字６が入るんですね。

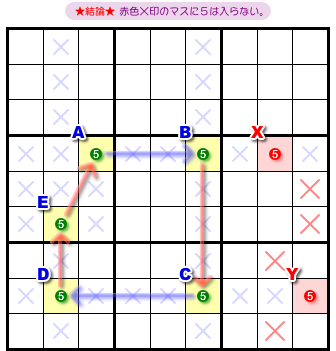
　図4-1 を見てみましょう。
　セクション２の盤面にさらにマスＹが増えています。
　リンクが奇数個なのは変わりませんが、今度は guardian が２つになりました。

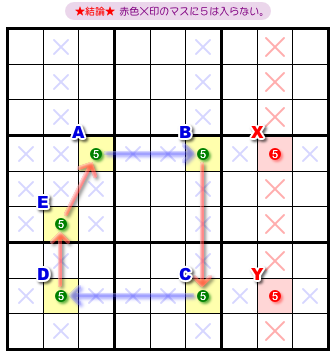
　この場合の結論はこうなります。

• マスＸ, Ｙ両方と列やブロックを共有しているマスがある。そのマスから guardian と同じ候補数字を除去できる。

　図4-1 だと、赤色×印の４マスが該当します。
　このマスに数字５は入りません。

　なぜこの結論になるんでしょう？
　それは、マスＸにもＹにも数字５が入らないとすると、破綻を引き起こしてしまうからです。
　悲劇のループができあがってしまうんですね。
　だから、Ｘ, Ｙのうち最低１つには必ず数字５を入れなきゃいけない。
　そうなると、×印のマスに数字５は入れられないんです。

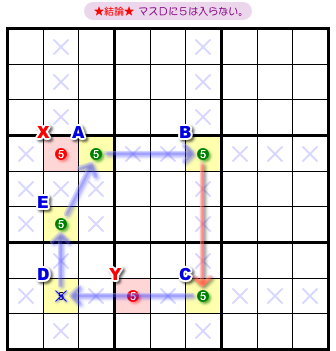
　次は、２マスＸ, Ｙが同じ列に属している形。
　結論はこうなります。

• ２マスＸ, Ｙの属する列において、Ｘ, Ｙ以外のマスから guardian と同じ候補数字を除去できる。

　図4-2 だと、赤色×印のマスが該当します。
　このマスに数字５は入りません。
　これも理由は同じ。
　マスＸ, Ｙのどちらかに必ず数字５が入るからです。

　図4-2 のように、guardian の位置によってはループ上のマスに影響が出たりするんですね。

　今度は、マスＸが弱いリンクを量産している形。
　結論はこうなります。

• マスＤから guardian と同じ候補数字を除去できる。

　理由は同じです。
　マスＸ, Ｙの少なくとも一方に必ず数字５が入るからなんですね。

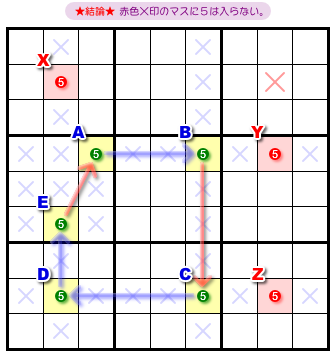
　最後は、guardian が３つある形。
　結論はこうなります。

• ３マスＸ, Ｙ, Ｚすべてと列やブロックを共有しているマスがある。そのマスから guardian と同じ候補数字を除去できる。

　理由は同じです。
　マスＸ, Ｙ, Ｚのうち最低１つに必ず数字５が入るからなんですね。

　例えば、セクション２では、guardian が守り神となってループを危機から救ってくれました。
　あの図を別の視点で考察してみましょう。

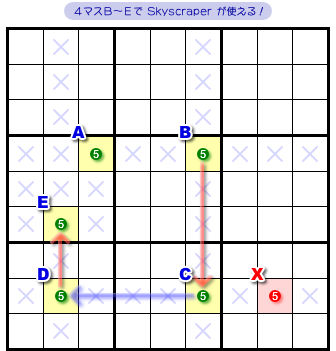
　図2-1 から強いリンクを２本取り除いてみます（図5-1）。
　強-弱-強 と３個のリンクが「コ」の字につながっていますね。
　この形をよく見ると…… なんと、解法 Skyscraper が使えるんです！

　あらま。
　じゃぁ、その解法をちょいと使ってみましょうか。

　Skyscraper により、赤色×印の６マスに数字５を入れられません。
　あら、マスＡに５は入らなくなったね。
　となると、マスＢとＥに５が入ることになるなぁ。
　さらに、マスＣとＤに５は入らなくなるよ。
　最後は、マスＸに５が確定しちゃった。

……あれ？
guardian さん、何にも仕事してなくね？

　guardian さんはループの守り役を担ってるはずでした。
　ところが、ループさんは普通に自己解決しちゃったんです。
　guardian さん、出る幕なし😅

　ル「自分でやっちゃいました〜！　すいませ〜ん！」
　ル「あ、ついでに guardian マスさんにも数字を入れときました！」
　ル「でも、これだと guardian さんに申し訳ないんで〜、guardian さんに守ってもらったという形で処理しときますんで〜！」
　ル「ありがとうございました〜〜！」
　ｇ「……」

　切ないぜ🥺