【解法】Death Blossom

　Death Blossom という解法は、中核となる１マスと複数の ALS を使った解法です。
　中核となる１マスにすべての ALS が結ばれているという状況で使い、すべての ALS に共通する候補数字がカギとなります。
　この解法を理解するためには、Almost Locked Set を理解する必要があります。
　（難易度：★★★★）

０．お花に見えますか？

　Death Blossom という解法には、「茎」と呼ばれる１マスと「花びら」と呼ばれる複数の ALS が登場します。
　そして、花びらはそれぞれ茎と候補数字１個でつながっています。

図 0-1

　Death "Blossom" ということで、しょーもない話をひとつ。
　すぐに解法 Death Blossom を知りたい方はセクション１に行っちゃってくださ〜い。

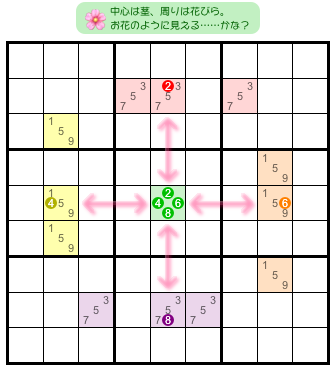
　図0-1 を見てみましょう（部分図です）。
　こういう状況になっています。

  • 茎は中央の 緑色１マス。花びらは４つの ALS。
  • 赤色 ALS と茎を結ぶ候補数字は２。同じタテ列に属する。
  • 黄色 ALS と茎を結ぶ候補数字は４。同じヨコ列に属する。
  • オレンジ色 ALS と茎を結ぶ候補数字は６。同じヨコ列に属する。
  • 紫色 ALS と茎を結ぶ候補数字は８。同じタテ列に属する。

　ちょうど茎の周りに花びらが付いていて、花を真正面から見ているかのよう！　キレイなお花です🥰

　図0-1 は作り物の Death Blossom で、この図からは何の結論も得られません。
　でも、なんとな～くお花っぽい雰囲気は受け取ってもらえた……かな？
　いかがでしょう？😄

１．どういう解法？

　残念ながら、現実の Death Blossom は前セクションのような綺麗な形はしていません。
　実際の Death Blossom はどういう解法なのか、解説していきましょう。

図 1-1

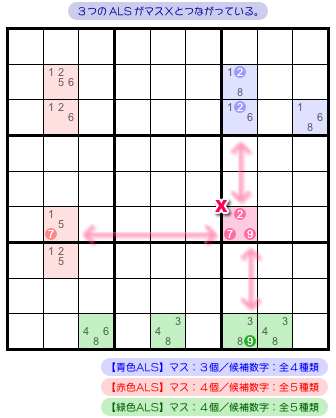
　図1-1 を見てみましょう（部分図です）。
　青色・赤色・緑色は ALS です。

  • マスＸ が茎。花びらは３つの ALS。
  • 青色 ALS と茎を結ぶ候補数字は２。すべて同じタテ列にある。
  • 赤色 ALS と茎を結ぶ候補数字は７。すべて同じヨコ列にある。
  • 緑色 ALS と茎を結ぶ候補数字は９。すべて同じタテ列にある。
  • マスＸ のすべての候補数字は ALS と１対１で結ばれている。
  • ３つの ALS には 候補数字６ が共通している。その候補数字は茎には存在していない。

　んもービジュアル的に理解しちゃった方が早い！
　マスＸを中心に ALS 達がつながっている。
　そんなイメージです。

　ちなみに、各 ALS にある候補数字２, ７, ９は、実質 RCC と同じ物だと考えてかまいません。
　実際、後に RCC と同様のはたらきをします。

　……え？　全然お花に見えない？
　現実なんてこんなモンさ😐

図 1-2

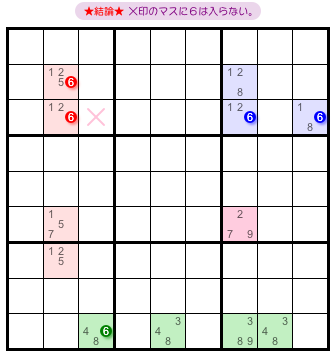
　前図1-1 からどういう結論が得られるんでしょう？
　こうなるんです。

  • ３つの ALS が持つすべての候補数字６と列やブロックを共有するマスがある。そのマスに数字６は入らない。

　図1-2 だと、×印のマスが該当します。
　このマスは６の２マスと同じヨコ列に属し、６の２マスと同じブロックに属し、マス６と同じタテ列に属しています。
　このマスに数字６は入らないというわけです。

　なぜ、こういう結論になるんでしょう？
　それは、候補数字６を持つ５マス６６６６６のどこかに必ず数字６が入るからなんです。
　それを解説しましょう。

図 1-3

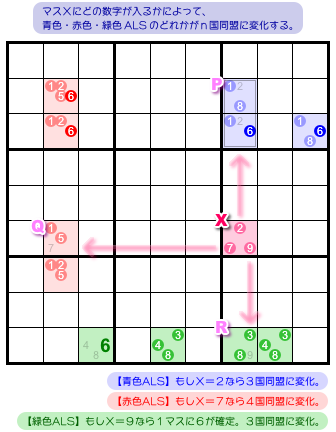
　マスＸには候補数字２, ７, ９がありますね。
　もちろん、そのうちのどれか１つが必ずマスＸに入ります。
　じゃぁ、実際に数字が入ったらどういう展開になるんでしょう？

　まず、２が入ったと仮定してみる。
　Ｘ＝２だから、Ｐの２マスに２は入りません。
　すると、青色 ALS は候補数字２を失って３国同盟（１６８の３国）に変化します。
　よって、２マス６のどちらかに６が入ることになりますね。

　次に、７が入ったと仮定してみる。
　Ｘ＝７だから、マスＱに７は入りません。
　すると、赤色 ALS は候補数字７を失って４国同盟（１２５６の４国）に変化します。
　よって、２マス６のどちらかに６が入ることになります。

　最後に、９が入ったと仮定してみる。
　Ｘ＝９だから、マスＲに９は入りません。
　すると、緑色 ALS は候補数字９を失って４国同盟（３４６８の４国）に変化します。
　ただ、緑色内部で３国同盟（３４８の３国）もできちゃってるもんだから、６は１カ所にしか入れられません。

　結局、何が言えるんでしょう？
　マスＸにどの数字が入ろうとも、こういう結果になるんです。

  • ３つの ALS のどれかには必ず数字６が入る。
図 1-4

　３つの ALS のどれかには必ず数字６が入る。
　ここからさらに話を展開していきましょう。

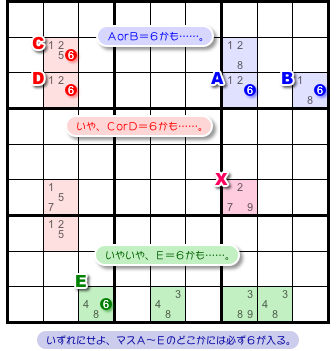
　候補数字６のあるマスをＡ〜Ｅとしておきます（図1-4）。
　この５マスに対して、次の３つのうち最低１つが成り立つんです。

  • マスＡ, Ｂのどちらかに数字６が入る。
  • マスＣ, Ｄのどちらかに数字６が入る。
  • マスＥに数字６が入る。

　これはもっと簡単に言えます。
　こうなるんです。

  • ５マスＡ〜Ｅのうち最低１カ所に数字６が入る。
図 1-5

　そうなると、数字６を入れられないマスが生じます。
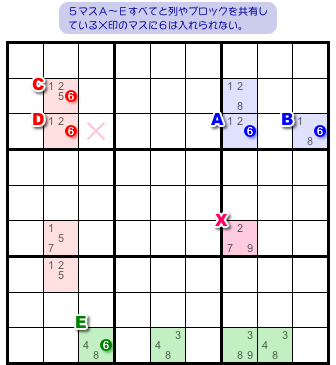
　×印を付けたマスです（図1-5）。
　このマスには次の特徴があります。

  • ５マスＡ〜Ｅすべてと列やブロックを共有している。

　×印のマスは２マスＡ, Ｂと同じヨコ列に属し、２マスＣ, Ｄと同じブロックに属し、マスＥと同じタテ列に属しています。
　前図1-4 で説明した通り６６６６６のどこかに必ず数字６が入るのだから、×印マスには数字６を入れることはできない。
　こういうわけなんです。

　図1-2 の結論通りになりましたね😊

２．実際に使ってみよう！

　実際の盤面で Death Blossom を使ってみましょう。
　花びらが２枚・３枚の場合をそれぞれ紹介します。

2-1．花びら２枚のパターン

図 2-1

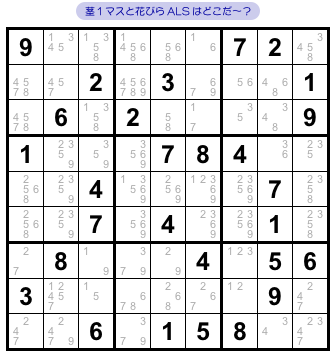
　まずは１つめの例です。

　図2-1 には、Death Blossom が使える箇所があります。
　そのためには、茎である１マスと花びらを表す ALS を探さなければいけません。
　さて、その茎と花びらはどこに潜んでいるでしょう？

図 2-2

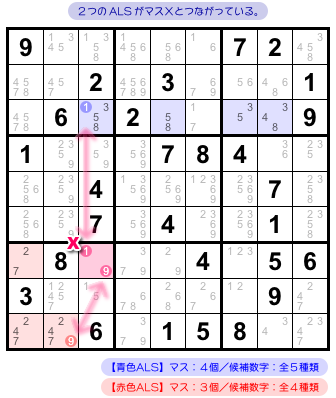
　茎と花びらは 図2-2 の通りです。

　確認してみましょう。
　こういう状況です。

  • マスＸ が茎。花びらは２つの ALS。
  • 青色 ALS と茎を結ぶ候補数字は１。すべて同じタテ列にある。
  • 赤色 ALS と茎を結ぶ候補数字は９。すべて同じブロックにある。
  • マスＸ の候補数字はすべて ALS と１対１に結ばれている。
  • ２つの ALS には 候補数字４ が共通している。茎には候補数字４は存在していない。

　青色＆赤色 ALS が茎とつながっていますね。
　２つの ALS は共通の候補数字を持っています。

　……っていうか、ちっともお花に見えない😅
　Death Blossom に見えないデス！（寒い）

図 2-3

　この場合はどういう結論が得られるんでしょう？
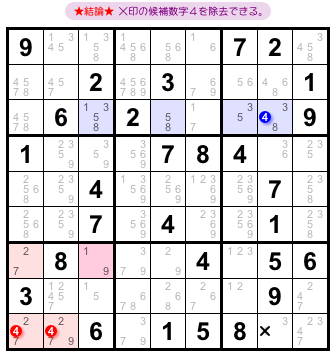
　こうなります。

  • 候補数字４を除去できるマスが１つある。

　図2-3、右下ブロックに存在します。×印を付けています。
　この１マスから候補数字４を除去できるんです。

　なぜこういう結論になるんでしょう？
　それは、候補数字４を持つ３マス４４４のどこかに必ず数字４が入るからなんです。
　それを解説しましょう。

図 2-4

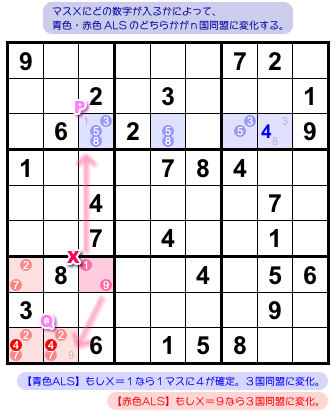
　マスＸには候補数字１と９がありますね。
　もちろん、どちらかが必ずマスＸに入ります。
　試しにそれぞれの数字が入ったと仮定してみましょう。

　まず、１が入ったと仮定してみる。
　Ｘ＝１だから、マスＰに１は入りません。
　すると、青色 ALS は候補数字１を失って４国同盟（３４５８の４国）に変化します。
　しかし、青色内部で３国同盟（３５８の３国）もできあがっている！
　というわけで、残った１マスに４を入れるしかありません。

　次に、９が入ったと仮定してみる。
　Ｘ＝９だから、マスＱに９は入りません。
　すると、赤色 ALS は候補数字９を失って３国同盟（２４７の３国）に変化し、赤色マスのどこかに４が入ることになりますね。
　つまり、２マス４のどちらかに４が入ります。

　両者を検証してみると、こういう結果になるんです。

  • 青色・赤色 ALS のどちらかには必ず数字４が入る。
図 2-5

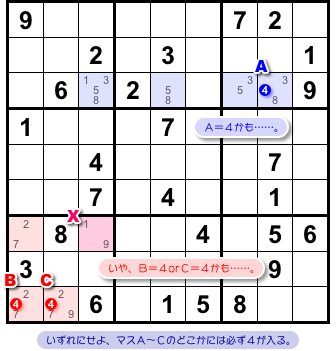
　２つの ALS のどちらかには必ず数字４が入る。
　前セクション同様に論理展開してみましょう。

　候補数字４のあるマスをＡ〜Ｃとしておきます（図2-5）。
　この３マスに対して、次のうち少なくとも一方が成り立つんです。

  • マスＡに数字４が入る。
  • マスＢ, Ｃのどちらかに数字４が入る。

　これはもっと簡単に言えますね。
　こうなります。

  • ３マスＡ〜Ｃのうち最低１カ所に数字４が入る。
図 2-6

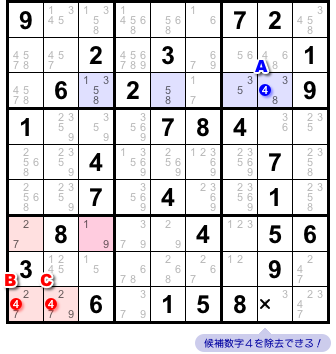
　そうなると、数字４を入れられないマスが生じます。
　×印を付けた１マスです（図2-6）。
　このマスには次の特徴があります。

  • ３マスＡ〜Ｃすべてと列を共有している。

　×印マスはマスＡと同じタテ列に属し、同時に、２マスＢ, Ｃと同じヨコ列に属しています。
　４４４のどこかに必ず数字４が入るのだから、×印マスには数字４を入れることはできない。
　こういうわけなんです。

　図2-3 の結論通りになりましたね😊

2-2．花びら３枚のパターン

図 2-7

　例をもうひとつ挙げてみます。
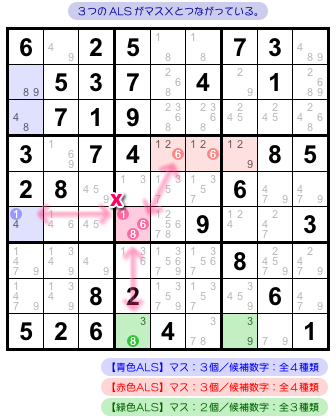
　今度は最初からお花を示します。

  • マスＸ が茎。花びらは３つの ALS。
  • 青色 ALS と茎を結ぶ候補数字は１。すべて同じヨコ列にある。
  • 赤色 ALS と茎を結ぶ候補数字は６。すべて同じブロックにある。
  • 緑色 ALS と茎を結ぶ候補数字は８。すべて同じタテ列にある。
  • マスＸ の候補数字はすべて ALS と１対１に結ばれている。
  • ３つの ALS には 候補数字９ が共通している。茎には候補数字９は存在していない。

　３つの ALS が茎とつながっていますね。
　各 ALS は共通の候補数字を持っています。

図 2-8

　この場合はどういう結論が得られるんでしょう？
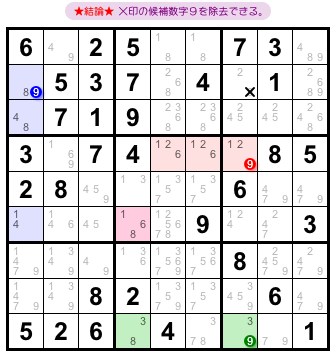
　こうなります。

  • 候補数字９を除去できるマスが１つある。

　図2-3、右上ブロックに存在します。×印を付けています。
　この１マスから候補数字９を除去できるんです。

　なぜこういう結論になるんでしょう？
　それは、候補数字９を持つ３マス９９９のどこかに必ず数字９が入るからなんです。
　それを解説しましょう。

図 2-9

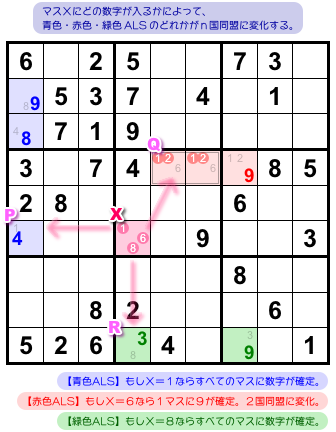
　マスＸには候補数字１, ６, ８がありますね。
　もちろん、どれかが必ずマスＸに入ります。
　試しにそれぞれの数字が入ったと仮定してみましょう。

　まず、１が入ったと仮定してみる。
　Ｘ＝１だから、マスＰに１は入りません。
　すると、青色 ALS は候補数字１を失って３国同盟（４８９の３国）に変化しま……っていうか、候補数字が少ないせいで３マスとも数字が確定しちゃいますね。０国同盟😊
　とりあえず、９の確定するマスが現れました。

　次に、６が入ったと仮定してみる。
　Ｘ＝６だから、Ｑの２マスに６は入りません。
　すると、赤色 ALS は候補数字６を失って３国同盟（１２９の３国）に変化する……んですが、Ｑの２マスで２国同盟発生！
　９の入り得るマスは１カ所しかなくなっちゃいました。
　その１マスに９が確定します。

　最後に、８が入ったと仮定してみる。
　Ｘ＝８だから、マスＲに８は入りません。
　すると、緑色 ALS は……青色 ALS と同じく２マスとも数字が確定します。これも０国同盟になった！
　９の確定するマスが現れます。

　全部検証してみると、こういう結果になりました。

  • ３つの ALS のどれかには必ず数字９が入る。
図 2-10

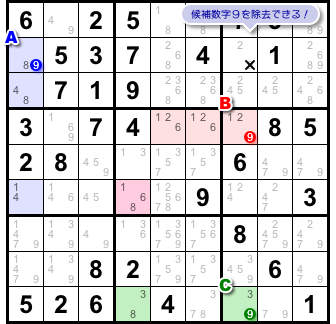
　３つの ALS のどれかには必ず数字９が入る。
　これをマス視点で見るとこう言い換えられますね。

  • ３マスＡ〜Ｃのどこかに必ず数字９が入る。

　そうなると、数字９を入れられないマスが生じます。
　×印を付けた１マスです（図2-10）。
　このマスには次の特徴があります。

  • ３マスＡ〜Ｃすべてと列を共有している。

　×印マスはマスＡと同じヨコ列に属し、同時に、２マスＢ, Ｃと同じタテ列に属しています。
　９９９のどこかに必ず数字９が入るのだから、×印マスには数字９を入れることはできない。
　こういうわけなんです。

　図2-8 の結論通りになりましたね😊

更新履歴