1.どういう解法?
Finned Swordfish の舞台は Swordfish と同じ。平行な3列。
その中の9マス+αが繰り広げる解法です。
9マスは Swordfish と同じくタテヨコに整列しているのに、+αのおかげで世界はまったく違います。
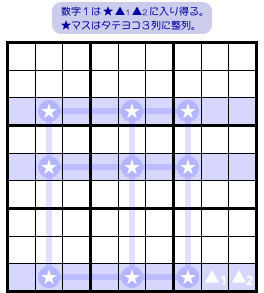
図1-1、青色3列を見てみましょう。
この3列において数字1の入り得るマスを探したら、次の状況だったとします。
- 青色3列において、★ ▲1 ▲2 の合計11マスにしか数字1は入らない。
- 9個の★マスはタテヨコ3列に整列している。
- ある1列には ▲1 ▲2 があり、1個の★と同じブロックに属している。
なんだか3行3列の整列に尻尾が生えちゃってるように見えますね。
これが Finned Swordfish の最大の特徴です。
これがあるだけで、Swordfish とはまったく異なる結論に至るんです。
ここで、用語をひとつ紹介しましょう。
図1-1 では尻尾のように付いた ▲1 ▲2 がありました。これを fin と呼びます。
fin は「ひれ」という意味です。
「ひれの付いた Swordfish」ということで、この解法には Finned Swordfish という名前が付いています。

さて、前図1-1 からはどういう結論が得られるんでしょう?
こうなるんです。
- ★マスの属するタテ列、▲1 ▲2 の属するブロック、この両者に共通する2マスがある。そのマスに数字1は入らない。
図1-2 だと×印の2マスが該当します。
この2マスは右側の★マス3つと同じタテ列に属しています。同時に、▲1 ▲2 と同じブロックに属しています。
この2マスに数字1は入らなくなるんですね。
なぜ、こういう結論になるんだろう?
それを解説していきましょう。

数字1の入り方について、大きく分けて2つの場合があります。
- ▲1 ▲2 のどちらかに数字1が入る。
- ▲1 にも▲2 にも数字1が入らない。
この両者についてそれぞれ検証していきましょう。
まずは前者。
これは簡単です。
▲1 ▲2 のどちらに数字1が入ろうとも、同じブロック全体に数字1が入らなくなります(図1-3 ×印)。
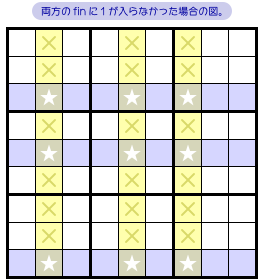
次に後者。
この場合は、fin がすべてなくなります。
あら、ただの Swordfish に姿が変わった!
ということは、Swordfish の結論の通り、★以外のすべての黄色マスに数字1が入らなくなりますね。
★以外の黄色マス、全滅!(図1-4)
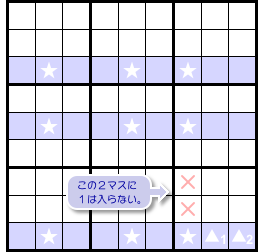
図1-3 と 図1-4、両者のうち一方が成り立ちます。
2つの図を見比べてみると……共通して×印のついているマスがありますね!
そのマスに数字1は入らないということが言えるんです。
具体的には 図1-5 の2マスです。
図1-2 の結論通りになりましたね😄
これが Finned Swordfish です。
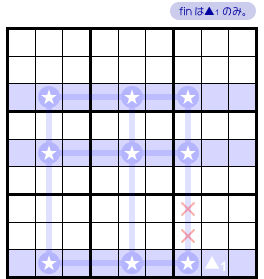
図1-1 では、fin は ▲1 ▲2 と2つありました。
実は、fin は1つしかなくてもかまいません。
この場合でも、まったく同じ論理展開ができます。
そのため、×印のマスに数字1を入れることができません。
ちなみに、fin が1つもない場合はただの Swordfish です。
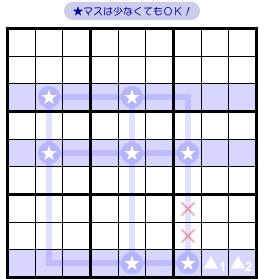
図1-1 では、9個の★がタテヨコ3列に整列していました。
しかし、本当は★がキッチリ9個並んでいる必要はありません。
★が少なくても、まったく同じ論理展開ができます。
大事なのは、★がタテにもヨコにも整列しているということです。
それさえ満たしていれば、★の個数は関係ありません。
上記の例では、青色はヨコ列でした。
もちろん、タテ列の場合でも理屈は同じです(その場合、fin はタテに並びます)。
その場合については、セクション2で実例を挙げて説明していきましょう。
このページは、単に Finned Swordfish の概要を知りたいという方々へ向けて書いたものです。
Finned Swordfish は Fish 系解法の一種ですが、Fish 系解法において重要な概念が2つあります。
それは ベースセット と カバーセット です。
どの Fish 系解法もその2セットを使って論理展開していくので、Fish 系解法を深く理解したければ2セットの理解は必須です。
この2セットによる Finned Swordfish を知りたい方々は Exofin のページをご覧ください。
2.実際に使ってみよう!
では、実際の盤面で Finned Swordfish を使ってみましょう。
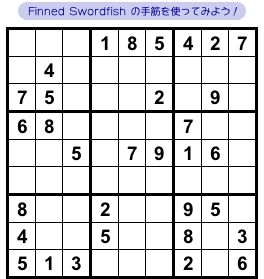
図2-1 では、とあるマスに数字が判明します。
それを Finned Swordfish で突き止めてみます。
ここでは数字4に注目して、4の入り得るマスを探してみます。
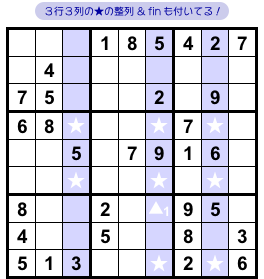
青色の3列に注目しましょう。
数字4の入り得るマスは 図2-2 の通りです。
★ ▲1 の合計9個。
8個の★を見ると、タテヨコ3列に整列しています。
そして、fin ▲1 も付いている。
さぁ、これはもぅ Finned Swordfish の出番です!
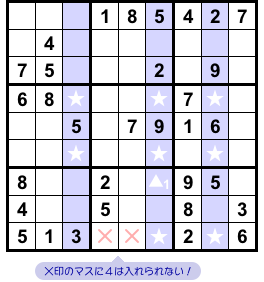
前セクションでの結論を 図2-2 に適用してみましょう。
すると、次のことが成り立ちます。
- ★マスの属するヨコ列、▲1 の属するブロック、この両者に共通するマスがある。そのマスに数字4は入らない。
理由は前セクションと同じです。
次の2通りに場合分けして検証すればOKです。
- ▲1 に数字4が入る場合。
- ▲1 に数字4が入らない場合。
というわけで、×印のマスに数字4を入れることができなくなりました。
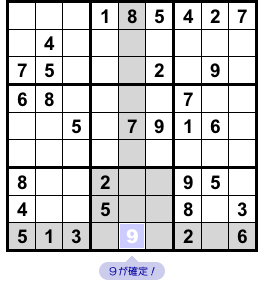
うまく Finned Swordfish が使えましたね!
もぅちょっと解き進めてみましょう。
図2-3 の×印マスのうち、右側の方に注目しましょう。
そのマスの属する列やブロック全域に目を通すと、そのマスの候補数字は4と9しかないことがわかります。
そして、×印マスに4が入らないことも既に判明しています。
というわけで、数字9が確定しちゃいました😄
更新履歴
- 2022. 2. 5.
- 新規公開。
- 2023. 3.31.
- ページ冒頭に難易度表記を追加。