1.Forcing Net とは何ぞや?
まずは、Forcing Net とは何かを説明しましょう!
……とは言ったものの、実はあんまり説明することがないんです。
なぜなら、Forcing Chain とほとんど同じだからです。
チェーンを使う解法だし、論理展開も Forcing Chain とまったく同じだし。
でも、Forcing Net という名前が付いているくらいなので、Forcing Chain とはちょっと違う。
はて、何が違うんでしょう?
このセクションでは、両者の違いを説明していきます。
以降、図の中には赤い矢印と青い矢印がありますが、それぞれ 強いリンク と 弱いリンク を表します。
まぁ、両者の違いは正直簡単です。
チェーンに枝分かれや合流があるか否か。
これだけ。
Forcing Chain で使われるチェーンはどれも一本道でした。
これは Forcing Chain だけでなく、X-Chain など他の解法でも一本道なんですね。
それに対して、分岐や合流のあるチェーンを使った Forcing Chain のことを Forcing Net と呼ぶんです。
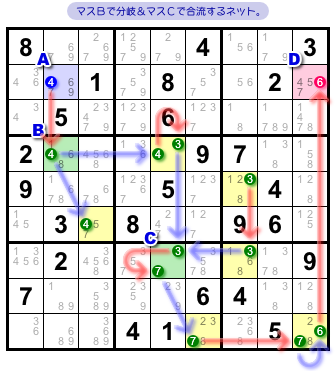
分岐・合流とは、具体的には 図1-1 のような形です。
マスAからDへとリンクが続いていますが、マスBの4で二手に分かれ、マスCの3で他のチェーンと合流してますね。
これが Forcing Net で使われるチェーンなんです。
もちろん、ただチェーンが分岐するだけでは Forcing Net を紹介する意味がありません。
分岐があるからこそできる論理展開もあるんです。
分岐チェーンの持つ特徴、ひとつ紹介しましょう!
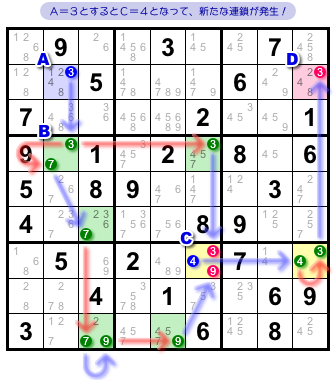
図1-2 には、マスAから始まるネットがあります。
マスBの3で左右に分岐した2本の流れはマスCに集結しています。
ここで、「マスAに数字3が入る」と仮定して二股のチェーンを伝っていくと、マスCには3も9も入れられなくなりますね。
ということは、マスCに4が確定することになる。
あれ?
そうなると、マスCの4からリンクを伝って別の連鎖が始まるんじゃない!?
そう。新たな連鎖が発生してマスDまで行っちゃうんです!
こういうふうに、分岐した道筋が同じマス・同じ列・同じブロックに再集結することで、新たに連鎖を生み出すことがあります。
Forcing Net では、こういった連鎖の自動発生もカギとなるんです。
次セクションでは具体例を使って解説していきますが、この連鎖自動発生が何回か起こります。
だから、このことは頭の片隅に入れておきましょう。
2.実際に使ってみよう!
次は、実際の盤面で Forcing Net を使ってみましょう。
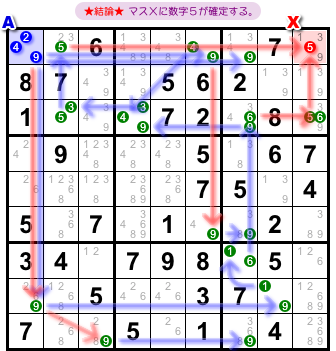
さて、いきなりですが結論を言っちゃいます。
- マスXに数字5が確定する。
え? もう結論?
まぁまぁまぁ、Forcing Net は図がゴチャゴチャになりやすいもんで結論を先にしてみました。
なんせ実際に使うチェーンは 図2-1 の通りでして😅
マス内部のリンクを省略してるのにゴッチャゴチャ😅
次を示すことで結論に導こうと思います。
- マスAにどの数字が入っても、必ずマスXに数字5が入る。
マスAには候補数字2, 4, 9がありますね。
そこで、2つに場合を分けて説明していくことにします。
- マスAに2または4が入る場合。
- マスAに9が入る場合。
ま、説明とは言っても、やることは「リンクをなぞるだけ」です。
同じ文言を繰り返すだけなので、読んでて飽きるかも😅
リンクを理解している方々なら、図だけでわかると思います。
サクッと読んじゃって(見ちゃって?)ください。
あっ、このセクションのメインは「b. マスAに9が入る場合」です。
a. はチェーンに分岐がありません。なので b. を重点的に解説していきます。
a. はテキトーにしゃべって終わらします😅
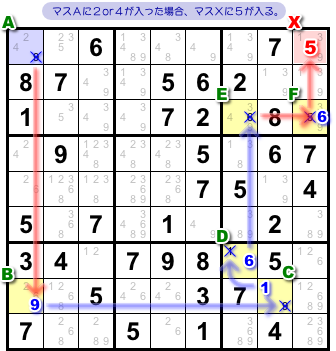
まずは「a. マスAに数字2または4が入る」場合。
テキトーにしゃべります。
A=2orA=4ということは、マスAに9が入らないということと同じです。
そう考えることにして、使うチェーンは 図2-2 の通り。
ただの一本道です😅
- マスAに9は入らない。
- 強いリンク によりマスBに9が入る。
- 弱いリンク によりマスCに9は入らない。1が入る。
- 弱いリンク によりマスDに1は入らない。6が入る。
- 弱いリンク によりマスEに6は入らない。
- 強いリンク によりマスFに6が入る。5は入らなくなる。
- 強いリンク によりマスXに5が入る。
というわけで、マスXに数字5が入りました。
めでたしめでたし。
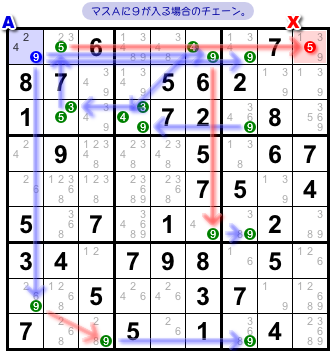
さぁ、次はいよいよメインです。
「b. マスAに数字9が入る」場合。
使うチェーンは 図2-3 です。
なんか結構複雑😓
もちろん、1つ1つ解説していきますよ〜!
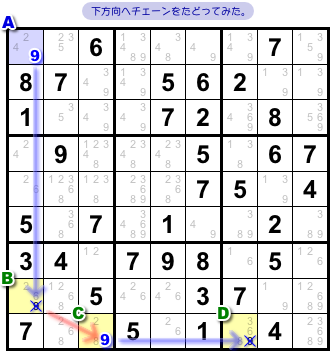
マスAの候補数字9からはルートが2種類あります。
まずは簡単な方を歩いてみましょう。
下方向の弱いリンクをたどってみます。
- マスAに9が入る。
- 弱いリンク によりマスBに9は入らない。
- 強いリンク によりマスCに9が入る。
- 弱いリンク によりマスDに9は入らない。
マスDに数字9は入りませんでした。
それがわかったところで、このルートはここで終わり。
マスAに戻って、もうひとつのルートを歩いてみましょう。
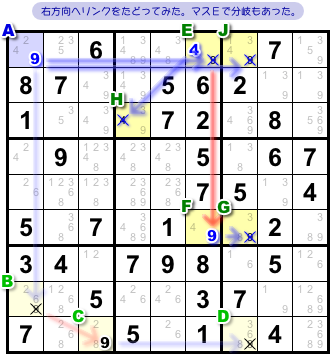
今度は、マスAから右方向へたどってみます。
- マスAに9が入る。
- 弱いリンク によりマスEに9は入らない。
- 強いリンク によりマスFに9が入る。
- 弱いリンク によりマスGに9は入らない。
また、マスEの候補数字9からは別ルートがあります。
手順 2. から続けます。
- 弱いリンク によりマスEに9は入らない。
- マスEに4が入る。
- 弱いリンク によりマスHに4は入らない。
ついでに、マスAからはこれも言えますね。
- マスAに9が入る。
- 弱いリンク によりマスJに9は入らない。
図2-5 では、マスEにルートが2つありましたね。
つまり、マスEの候補数字9からチェーンは二手に分かれていた。
これが Forcing Net の大きな特徴なんです。
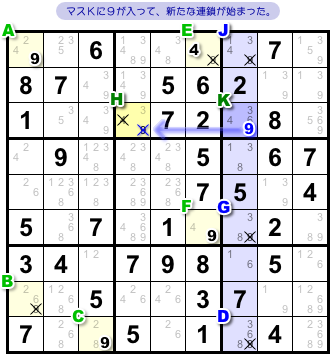
なんだか候補数字が結構除去されてきましたね。
ここで、青色タテ列に注目してみましょう。
さて、数字9の入るマスはいくつあるでしょうか?
実は、たった1つしかない!
3マスD, G, Jの候補数字9がことごとく除去されてしまって、1マスしか残っていなかったんです。
というわけで、マスKに数字9が入ることになりました。
しかも、よく見ると……マスKの候補数字9から弱いリンクが出ているじゃぁないですか!
- マスKに9が入る。
- 弱いリンク によりマスHに9は入らない。
マスKから新たに連鎖が始まった!
これが、前セクションで述べた「連鎖の自動発生」なんです。
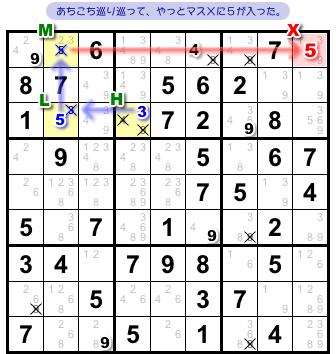
さて、マスHを見てみましょう。
マスHの候補数字4は既に消えていました。
そして、候補数字9はたった今消えた。
マスHには数字3を入れるしかなくなっちゃいました。
しかも、マスHの候補数字3からは弱いリンクが出ています。
連鎖の自動発生再び!
ここから先はリンクに沿って歩くだけです。
ゴールまであと少し!
- マスHに3が入る。
- 弱いリンク によりマスLに3は入らない。5が入る。
- 弱いリンク によりマスMに5は入らない。
- 強いリンク によりマスXに5が入る。
やっとマスXにたどり着きました。
もぅあっちこっち回りましたね!
この場合もマスXに数字5が入りました。
というわけで、図2-1 の結論通りになりました😊
更新履歴
- 2022. 2. 5.
- 新規公開。
- 2023. 3.31.
- ページ冒頭に難易度表記を追加。