１．ナンプレは解を１つしか持たないパズルである
雑誌やスマホアプリなどで世に出ているナンプレを解いていくと、すべてのマスが数字で埋まって解き終えることができますね。
これは「ナンプレの解はただ１つしかない」ということを意味しています。
しかし、実は、ナンプレのルールには「解は１つしか持たない」という文言がありません。
タテ・ヨコ・ブロックに関するルールはあるけれど、解の個数については明記されていないんですね。
でも、何百何千と解いてきた方々でも、複数解を持つナンプレを目にしたことはほとんどないと思います。
あったとしてもそれは出題者側のミスで、後にお詫びが掲載されたりする。
というのも、ナンプレは「解は必ずただ１つ」が原則であり、複数解を持つナンプレは良い作品とは認められないからなんです。
そうなると、その原則に則った解法が考え出されてもおかしくありません。
解はただ１つしかない。
じゃぁ、複数解が生じるような理屈はおかしいんじゃない？
こういうわけですね。
そういう観点から Unique Rectangle や Bivalue Universal Grave などの解法が生まれていきました。
実は、複数解を利用した解法は多く存在します。
そして、各解法の対象となる複数解パターンもいろいろ存在します。
そこで、次セクションではいろんな複数解パターンを紹介していきましょう。
複数解に関連して unavoidable set という概念もあるので、それも紹介します。
【追記】なぜ複数解を持つナンプレは良い作品とは認められないのか？
なぜ複数解を持つナンプレは良い作品とは認められないのか？
その理由を説明しましょう。
ま、手っ取り早く言うと「そんなナンプレは面白くないから」です。
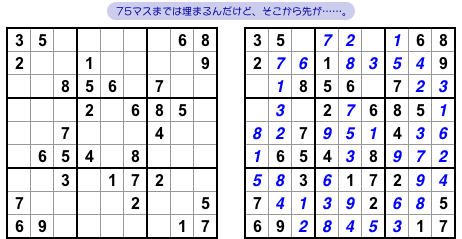
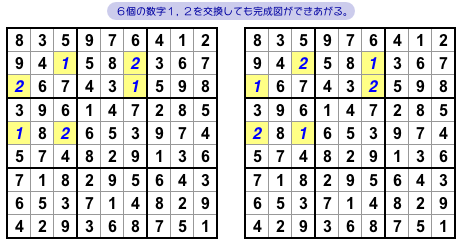
図1-1 左側のナンプレを解くと、図1-1 右側のように75マスまで埋まります。
しかし、ここで困ったことが起こる。
どうしてもここから先へ進めない。
なぜかと言うと、空きマスの１つに数字４を入れても９を入れても完成できてしまうから。
どちらを入れてもＯＫなんですね。
しかし、それは「マスに入る数字を論理的には決定できない」ということも意味します。
つまり、完成目前というところで理詰めが頓挫してしまったわけです。
「最後まで理詰めで解ける」
ナンプレなどの数理系パズルにおいて、これは最も重要です。
各マスに入る数字を論理的に突き止め、その積み重ねで解き進めていき、すべてのマスが埋まって完成する。
理詰めでゴールできた達成感が楽しいわけで、これは数理系パズルの要と言えるものなんです。
しかし、複数解を持つナンプレはその楽しさを奪います。
図1-1 のように必ず論理の流れが途絶えてしまい、完成には至らないからです。
どんなに正しく解き進んでいても途中で断念を余儀なくされ、達成感は得られない。
これじゃぁ面白さが半減しちゃうんですね。
だから、ナンプレ制作者達は複数解のあるナンプレを作りません。
ちなみに、「最後まで理詰めで解ける」とはどういうことか？
少し具体的に言うとこういうことです。
「このマスはこの数字で確定する」
これが最後の１マスまで論理的に続く。
解いている途中のどの局面であっても、数字の確定する空きマスがどこかに必ずある。
そのマスを理詰めで見つけ、数字を入れる。
これが最後まで繰り返されて完成にたどり着く。
こういうことです。
そうやってできたナンプレには複数解はありません。
どのマスにもただ１つの数字が確定してるわけですもんね。
ナンプレは必ず完成でき、達成感が必ず味わえる。
これが数理系パズルの正しいあり方です。
制作者達は「最後まで理詰めで解ける」ことを必ず心掛けてナンプレを作っています。
２．複数解の起こるパターン
「複数解が起こらない！」ということを根拠にした解法がナンプレには数多く存在します。
ただ、その前に「複数解とは何ぞや？」というところから話をしなきゃいけません。
そこで、このセクションでは、複数解の起こってしまうパターンについて解説していきます。
2-1．最も簡単な複数解パターン
まず、最も簡単な複数解パターンを紹介します。
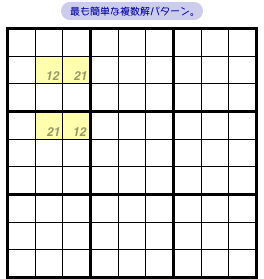
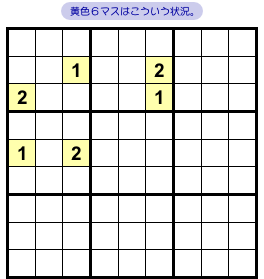
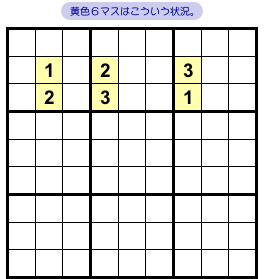
図2-1、黄色４マスが矩形状に並んでいますね。
この４マスは次の状況になっています。
- 黄色４マスは、タテ２列・ヨコ２列・ブロック２個にのみ属している。
- どの黄色マスも候補数字は２つだけ。しかも、すべて同じ。
黄色マスを含むヨコ列は２つあります（２行目と４行目）。
黄色マスを含むタテ列は２つあります（２列目と３列目）。
黄色マスを含むブロックは２つあります（左上隅とそのすぐ下）。
そして、黄色４マスはすべて数字１と２しか入れられません。
こういう特徴があるんですね。
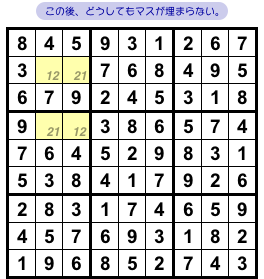
ナンプレを解く上で、前図2-1 のような箇所があると不都合が生じます。
最後まで解き終えることができないんです。
一応、うまいこと解き進められれば、図2-2 のように 77マスまでなら数字で埋められるかもしれません。
ところが、これ以上マスが埋まらない。
どうしてもここから先へ進めない！
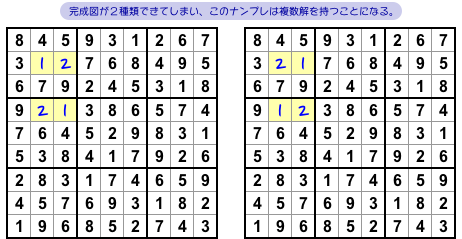
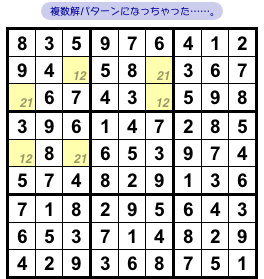
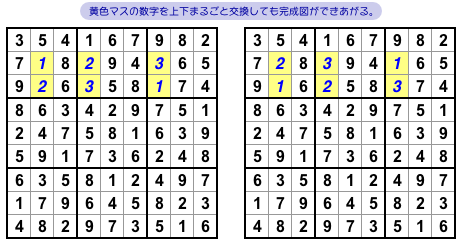
それもそのはずで、前図2-2 の状況からは完成図を２種類作ることができるんです。
図2-3 の通り。
黄色マスのどれか１つに数字１を入れても数字２を入れても完成できてしまう。
もちろん、両者の完成図は異なるから、解が複数あるわけなんです。
結局、図2-1 の状況が生まれてしまった時点で、そのナンプレは必ず複数解を持つ。
これはどうしても免れないんです。
「このマスはこの数字で確定する！」
これが最後の１マスまで続くから、ナンプレは完成まで解き進めることができます。
ところが、複数解パターンがあるとその流れは途絶えてしまう。
なぜなら、図2-2 のように数字の確定できる空きマスが１つもなくなってしまうから。
どうしてもゴールにはたどり着けないんです。
論理的にゴールにたどり着いてもらうために、ナンプレは必ず唯一解を持つように作られています。
そのようなナンプレを解いている時、複数解パターンが現れることは絶対にないんです。
前図2-3 に関連して、もうひとつ注意すべきことがあります。
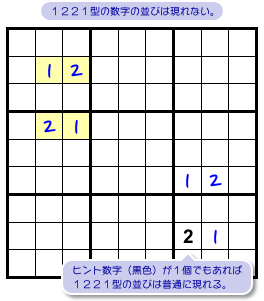
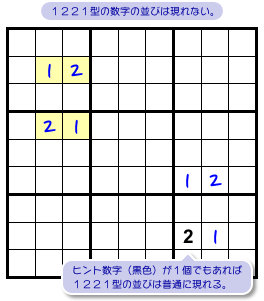
- 解いている途中で 図2-4 左上のような数字の並びは絶対に現れない。
この黄色４マスの数字はヒント数字（問題図に最初からある数字）ではなく、解いている途中で書き込まれた数字です。
何もないところから１２２１の形は生まれないということですね。
なぜかというと、たとえこの状態から 前図2-3 左側のように完成したとしても、この４マスの１と２を交換して 図2-3 右側の形にもできてしまうからです。
１２２１の形がある時点で、もう複数解は免れないんですね。
だから、この１２２１型の並びは現れません。
ただし、図2-4 右下のように４つのうち最低１つがヒント数字（黒色）だったなら、１２２１型は普通に現れます。
「複数解はＮＧ」という視点で見ると、図2-1 も 図2-4 も致命的な状況だと言えます。
だから、その状況を逆手に取った理屈が思い浮かび、それが解法へと発展していった。
現に、図2-1 からは解法 Unique Rectangle が生まれ、図2-4 からは解法 Avoidable Rectangle が生まれています。
ちなみに、図2-4 の形は両方とも unavoidable set と呼ばれます。
あまり深く覚える必要はありませんが、知りたい方々はセクション３をご覧ください。
2-2．他の複数解パターンもあるよ！
マス数が増えた複数解パターンも紹介しましょう。
例を２つ挙げて解説します。
まずは１つめ。
このような形は解法 BUG Lite に登場します。
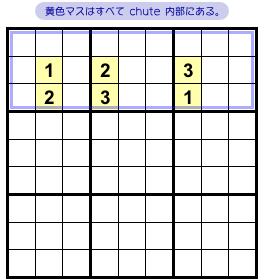
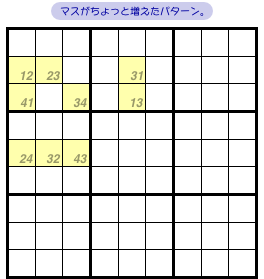
図2-5 を見てみましょう。
４マスからちょっと増えました😊
マスがこぢんまりと並んでいますが、黄色全体を見ると次の特徴があります。
- どの黄色マスを見ても、候補数字は２つしかない。
- 黄色マスを持つどの列やブロックを見ても、黄色マス内部の候補数字はそれぞれ２回ずつしか現れない。
例えば、左端のタテ列には黄色マスが３つありますが、その候補数字１, ２, ４はそれぞれ２回ずつ現れています。
左上ブロックでは候補数字１〜４が２回ずつ現れていますね。
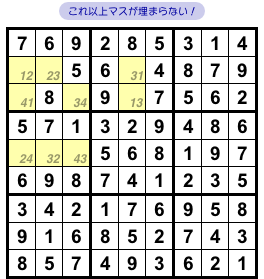
この場合も、うまく解き進められれば 図2-6 のように白マス全部を埋められるかもしれません。
しかし、やっぱりこれ以上マスが埋まらないんです。
どうしても先へ進めない😞
図2-6 からも完成図は２種類できあがります。
このナンプレも複数解を持つんですね。
２つめの例。
このような形は解法 Bivalue Universal Grave に登場します。
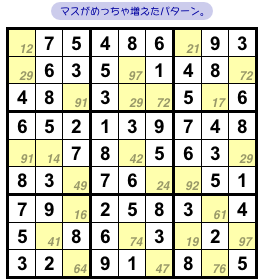
図2-7 です。
さらに多くなりました。
なんと、黄色マスは 20個以上！
これだけあっても、図2-5 と同じ特徴を持っているんです。
- どの黄色マスを見ても、候補数字は２つしかない。
- 黄色マスを含むどの列やブロックを見ても、黄色マス内部の候補数字はそれぞれ２回ずつしか現れない。
図2-7 からも完成図は２種類できあがります。
このナンプレも複数解を持つんですね。
2-3．複雑な複数解パターン
今までは、どのマスも候補数字が２個しかありませんでした。
もちろん、３個以上の場合でも複数解パターンは存在します。
ただ、それを活用する解法はほぼ無いので、紹介だけ。
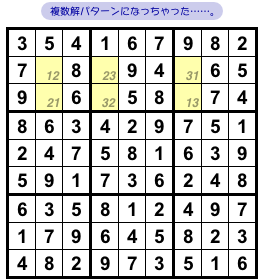
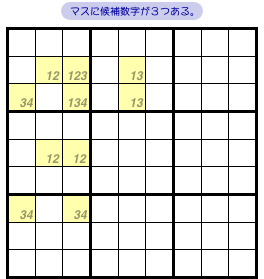
例えば 図2-8 ですね。
この黄色10マスには候補数字１〜４が散らばっていますが、今までのようなハッキリとした特徴はありません。
図2-8 から白マスをすべて埋めたとしても、完成図は５種類できあがります。
やはり、このナンプレも複数解を持ってしまうんですね。
最後に、複数解ＮＧを根拠とする解法についてちょいと真面目な話をひとつ。
複数解がＮＧだとはルールで規定されていません。
「必ず唯一解を持つ」というのは、作り手たちの持っている共通認識に過ぎないんですね。
だから、ルールにも書かれていない勝手な認識を解き手に要求するというのは、本当はおかしな行為です。
そういう意味で、Unique Rectangle など唯一解を拠り所とする解法は本筋であるとは言いづらいんですね。
作り手の立場からすると、こういう裏筋の解法を必須とするナンプレ問題は作るべきではありません。
しかし、解き手の立場で見ると話はガラッと変わります。
ナンプレを解く時に、皆さんはいちいちそんな裏事情を気にする必要はありません。
本筋だの裏筋だのは正直ど〜でもいい話。
楽しく解けりゃぁそれで良いのです😊
逆に、解き手だけでなく作り手の視点も味わえる。これもまたナンプレの面白いところですね。
裏事情ひとつでナンプレの世界をさらに知る。これもまたオツなものです。
３．Unavoidable Set
複数解パターンの他にも、数字の並びに複数解が関係することもあります。
それについて解説していきます。
3-1．unavoidable set とは何ぞや？
図3-1 を見てみましょう。
こぢんまりと散らばった黄色６マスに数字が入っていますね。
黄色全体を見ると、次の状況になっています。
- どの黄色マスにも数字１, ２どちらかが入っている。
- 黄色マスの属するどの列やブロックを見ても、黄色マスは２つある。さらに、その２マスには数字１, ２が１個ずつ入っている。
例えば、左端タテ列には黄色マスがちょうど２つありますね。
その２マスには数字１と２が１個ずつ入っている。
これは、黄色マスの属する列・ブロックすべてに言えることです。
実は、この黄色６マスには大きな特徴が１つあるんです。
数字を交換しても完成図ができる！
他のマスを全部埋めると、図3-2 左側のように完成図ができあがります。
そこから黄色マスの１と２を交換してみると、図3-2 右側のようになる。
あら、これも完成図になってるよ！
白マスの数字はそのままに、黄色６マスをいじるだけで別の完成図を作れるんですね。
図3-2 の黄色マスのように、数字を交換してもまた完成図になれる。
黄色マスのこのような数字配置を unavoidable set と呼びます。
ここで、unavoidable set の性質を１つ紹介しましょう。
複数解に関する性質です。
実は前セクションの 図2-4 で軽く触れてはいますが、図3-4 でもう一度解説します。
今、黄色６マスがすべて空きマスだったとしましょう（図3-3）。
この盤面、どういう状況になっているでしょうか？
あぁ……こりゃ非常にマズい！
複数解パターンになってしまってる😞
そう、数字を全部取っ払うと複数解が生じてしまうんです。
もちろん、これはＮＧです。
ということは、作り手の立場からすると複数解を回避する手段が必要になる。
具体的には、どれかの黄色マスにヒント数字を置かなきゃいけません。
というわけで、こういうことが成り立つんです。
- どの unavoidable set にも必ずヒント数字が存在する。
unavoidable set はヒント数字を最低１つ抱えなきゃいけない。
逆に言えば、ヒント数字のない unavoidable set は存在してはならない。
こういうことなんですね。
それを踏まえて、前セクション 図2-4 の盤面をもう一度（図3-4）。
これを unavoidable set の視点でおさらいしましょう。
左上の黄色４マス、これは unavoidable set です。
そして、どの数字もヒント数字ではありません。
この形はマズいんですね。複数解パターンが生じてしまうから。
こういう set はあってはならないんです。
対して、右下の４マス、これも unavoidable set です。
ただ、今度はヒント数字がありますね。
この４マスからは複数解は生じません。
こういう set はあってもＯＫなんです。
図3-1 のような形の unavoidable set は、解法 Reverse BUG で使われます。
詳細は Reverse BUG のページをご覧ください。
3-2．２列に存在する unavoidable set
実は、unavoidable set には他の形も存在します。
それを解説しましょう。
図3-5 を見てみましょう。
黄色６マスが整列しているように見えますね。
黄色全体を見ると、次の状況になっています。
- 黄色マスはヨコ２列にのみ存在している。また、その２列は同じ chute に属している。
- 黄色マスの属するどのタテ列を見ても、黄色マスが２つある。
- ヨコ２列とも、黄色マスに入っている数字の組み合わせは同じである。
黄色マスは上から２行目＆３行目に存在しています。
そして、どちらのヨコ列も黄色マス内部の数字は１〜３ですね。
「chute」については 図3-7 で説明することにしましょう。
実は、この黄色６マスには大きな特徴が１つあるんです。
数字を交換しても完成図ができる！
他のマスを全部埋めると、図3-6 左側のように完成図ができあがります。
そこから黄色マスの数字を上下まるごと交換してみると、図3-6 右側のようになる。
おぉ、これも完成図になってるじゃぁないか！
白マスの数字はそのままに、黄色６マスをいじるだけで別の完成図を作れるんですね。
図3-6 の黄色マスのように、数字を交換してもまた完成図になれる。
このような数字配置も unavoidable set なんです。
そういえば、新しい用語が現れていましたね。
「chute」です。シュートと読みます。
さて、chute とは何ぞや？
chute とは、ブロック３個並んだ３×９マスの領域です。
chute にはヨコ長とタテ長の２種類があります。
３×９のヨコ長の chute を floor と呼びます。
９×３のタテ長の chute を tower と呼びます。
図3-7 では、ヨコ２列とも青枠の floor に存在しているわけですね。
実は、２列から生まれる unavoidable set において、その２列は次の条件を満たさなければいけません。
- ２列とも同じ chute 内部に存在する。
２列が同じ chute 内部にないと、前図3-6 のような数字交換はできません。
ご注意ください。
セクション3-1でも解説しましたが、ここでも unavoidable set の性質をご紹介。
複数解に関する性質です。
今、黄色６マスがすべて空きマスだったとしましょう（図3-8）。
この形、非常にマズいですね！
複数解パターンになってしまってる😞
図3-3 と同様で、数字を全部取っ払うと複数解が生じてしまうんです。
もちろんこれはＮＧ。
図3-3 と同様にヒント数字を配置する必要があります。
というわけで、こういうことが成り立つんです。
- どの unavoidable set にも必ずヒント数字が存在する。
unavoidable set はヒント数字を最低１つ抱えなきゃいけない。
逆に言えば、ヒント数字のない unavoidable set は存在してはならない。
こういうことなんですね。
この形の unavoidable set は、解法 Reverse BUG Lite で使われます。
詳細は Reverse BUG Lite のページをご覧ください。
3-3．複雑な unavoidable set
今までは、簡単な unavoidable set を紹介しました。
数字が２種類だけだったり、２列だけだったり。
もちろん、さらに複雑な unavoidable set は存在します。
ただ、それを活用する解法はおそらく無いので紹介だけ。
例えば 図3-9 ですね。
この黄色９マスに並んだ数字１〜４です。
この９つの数字を適度に交換すると別の完成図ができあがります。
ちなみに、図3-9 の黄色マスがすべて空きマスだったとすると、前セクションの 図2-6 になります。
unavoidable set のどこかにヒント数字がなければ複数解が生じてしまう、ということの一例になっています。
更新履歴
- 2022. 2. 5.
- 新規公開。
- 2022.11.14.
- セクション１に「なぜ複数解を持つナンプレは良い作品とは認められないのか？」を追記。
- 2023. 3.31.
- ページ冒頭に難易度表記を追加。