1.どういう解法?
ナンプレを解いていると、マスが数字で埋まっていきますね。
そして、空きマスがどんどん少なくなっていく。
空きマスを全部なくせば完成ですが、当然、途中過程は必ずあります。
空きマスが少し残っている状態ですね。
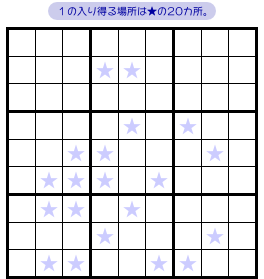
例えば、数字1の入り得るマスが 図1-1 みたいに20カ所程度残っている。
途中過程でこういった状況は毎回あるわけですね。
- 盤面全体において、数字1は★マスにしか入らない。
パッと見だと、これだけでは数字1の確定するマスは見つからなさそう。
でも、実は、数字1に関していくつか判明するんです。
果たして、何がどう判明するんでしょう?
ちょっとこんなことを考えてみましょう。
「数字1の入り方のパターン、全部挙げてみようか!」
なんと、試しに数字1をマスにアレコレ入れてみて、数字1の入り方を全パターン見つけちゃおうというのです。
すっごい原始的😓
まぁでも、実際にやってみましょうか。
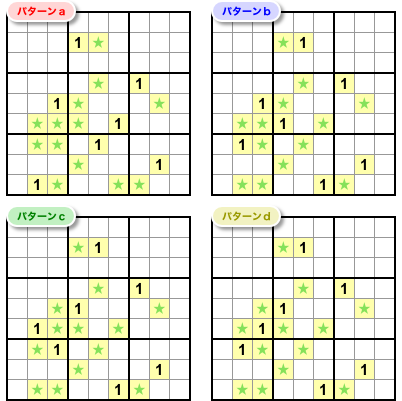
数字1のパターンは全部で4通り。図1-2 です。
a〜dと名前を付けておきましょう。すぐ後の 図1-4 で使います。
ここからこの4パターンを見て考察していきます。
これらのパターンを見てみると、数字1が入っているマスもあれば、数字1の入っていないマスもありますね!
……って、何を当たり前なこと言ってるんだ😓
まぁそれはおいといて。
さらに次のようなことに気付いたりすると、また見え方が違ってくるかもしれません。
そういや、一度も数字1の入らなかった★マスがチラホラあるなぁ。
これに気付けば、解法 Pattern Overlay Method の基礎は半分理解できたようなもの。
実は、この解法のキモはそういったところにあるんです。
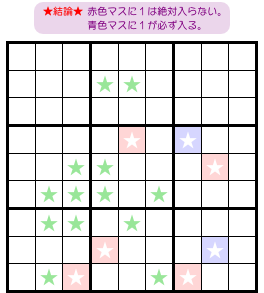
では、結論を言いましょう。
結論は2つあります。
- どのパターンにも数字1が現れなかった★マスには、数字1は入らない。
- どのパターンにも数字1が現れた★マスには、数字1が確定する。
図1-3 だと、a. に該当するのは赤色マスです。
b. に該当するのは青色マスです。
赤色マスに数字1は絶対に入りません。
青色マスに数字1が確定します。
数字1に関して、7マスに影響が出るというわけです。
なぜこういう結論になるのか?
それを説明していきましょう。
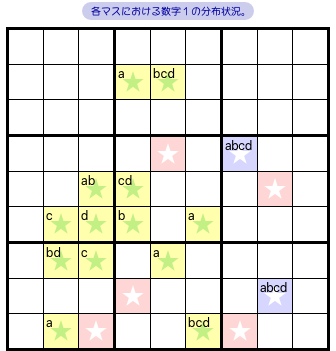
全パターンをもう一度示して説明することもできますが、ここでは別の方法で説明してみます。
図1-2 で4パターンa〜dを紹介しましたね。
数字1の入った★マスにa〜dをメモしてみます。
パターンaの中で数字1のあるマスに「a」をメモする。
b, c, dも同様にメモしていく。
すると、図1-4 の通りになりました。
この時、次のことに気付きます。
- 赤色マスにはメモがまったくない。
- 青色マスはa〜dすべてメモされている。
ナンプレが完成した時、数字1はパターンa〜dのどれか1つの形に配置されることになります。
しかし、a〜dのどれが採用されようとも赤色マスに数字1が入ることは絶対にないんですね。そして、青色マスには数字1が必ず入ることになるんです。
ということは、「赤色マス≠1」「青色マス=1」の2つはもう既に保証されているわけなんですね。
図1-3 の結論通りになりました😊
これが Pattern Overlay Method という解法です。
2.実際に使ってみよう!
次は、実際の盤面で Pattern Overlay Method を使ってみましょう。
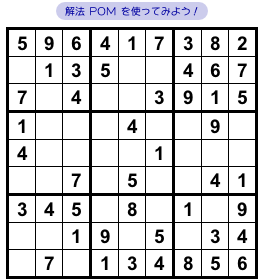
空きマスの数が少ない方が Pattern Overlay Method を使いやすいです。
だから、終盤の盤面(図2-1)で解説しましょう。
……とか言っといて、全然終盤じゃないじゃん😅
あ、いやその、数字7に関しては終盤を迎えつつあります😅
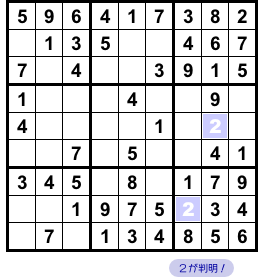
図2-1 の時点では、もぅ数字7の入るマスがかなり少なくなっています。
そこで、Pattern Overlay Method で7の場所を突き止めてみます。
まずは、7の入り得るマスを洗い出しましょう!
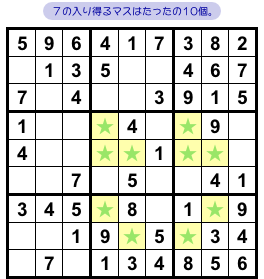
数字7の入り得る場所は★マスです(図2-2)。
たったの10カ所!
見るからにこぢんまりとした分布ですね。
特に、★マスを2個しか持たないタテ列・ヨコ列・ブロックが多い。
これがすごく大きくて、おかげでパターン数はグッと絞られます。
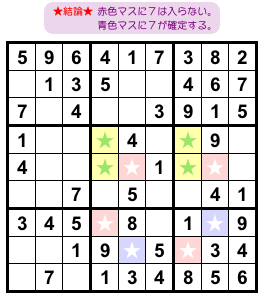
さぁ結論です。
図2-2 からはこうなります。
- 4マスに数字7を入れられなくなる。
- 2マスに数字7が確定する。
図2-3 だと、赤色&青色の6マスが該当します。
赤色マスに数字7を入れられなくなります。
青色マスに数字7が確定します。
これは、全パターンを挙げれば一発でわかります。
早速挙げてみましょう!
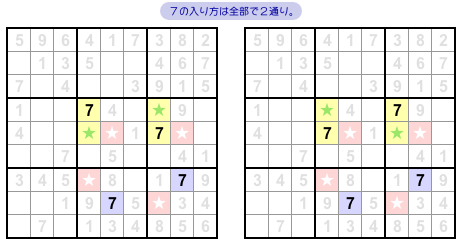
実は、数字7の入れ方はたった2通りしかありません。
図2-4 の通りです。
この2パターンを見れば一目瞭然ですね!
赤色マスには数字7はまったく入っていないし、青色マスには必ず数字7が入っている。
図2-3 の結論通りになりますね😊
マスが少なくて分布がこぢんまりとしていると、2〜3パターンで済んだりします。
そのくらいだと、人によっては頭の中だけで処理できるかもしれませんね。
うまく Pattern Overlay Method が使えましたね!
もぅちょっと解き進めてみましょう。
数字7を入れた後、タテ列やブロックを見れば他のマスにも容易く数字が入っちゃいますね😄
3.複数の数字が関係するパターン
今までは、1種類の数字にのみ注目して話をしていきました。
今度は複数の数字に注目するパターンを紹介します。
……と、本題の前に前準備をひとつ。
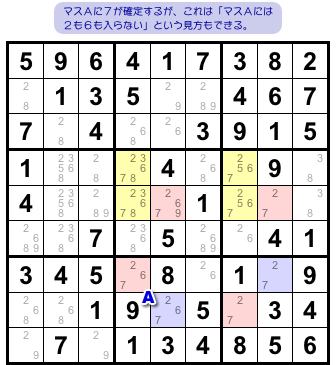
前セクションで使った盤面をもう一度見てみましょう(図3-1)。
これを候補数字の視点で軽く考察します。
前セクションでは、候補数字7を持つ10マスに注目して「青色マスに7が確定する」と結論づけました。
これは、他の候補数字からの視点では「マスAには2も6も入らない」といったことも言えるわけですね。
図3-1 では数字6の入り得る場所は 20マスほどあるから、6の入れ方のパターンは数多くあります。
その中には、マスAに6の入るパターンも含まれている。
ところが、マスAに6は入れられなくなった。
ということは、数字6のパターンはその分減ることになるんですね。
つまり、数字7のパターンによって数字6のパターンが減らされたと言えるわけです。
実は、「数字aのパターンによって数字bのパターンが減ってしまう」という現象が起こったりするんです。
そして、パターンが減らされたことで数字bに新展開が起こる。
このセクションでは、そういう話をしていこうと思います。
原案は Sudopedia のミラーサイト、Pattern Overlay Method のページです。
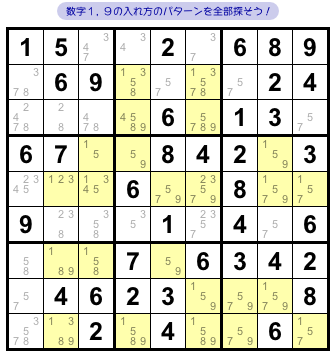
新しい盤面を用意しましょう。
図3-2 です。
この盤面では2つの数字1と9に注目します。
そして、各数字の入れ方のパターンを洗い出してみます。
候補数字1と9は 図3-2 の黄色エリア内部に分布しているので、これらの配置を基にパターンをそれぞれ全部見つけましょう。
詳細は省きますが、数字1も9もパターンは5個ずつ見つかります。
数字1の方はA〜E、数字9の方はa〜eと名付けておきましょう。
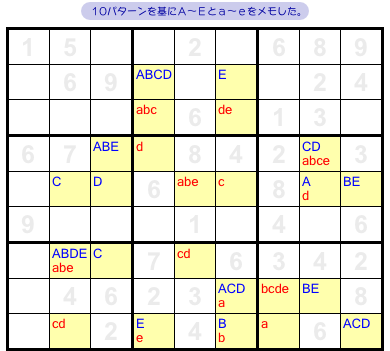
次は、その見つけた全10パターンを基に盤面にメモしていきます。
パターンAの中で数字1のあるマスに「A」をメモします。
パターンBの中で数字1のあるマスに「B」をメモします。
C〜Eも同様にメモします。
パターンaの中で数字9のあるマスに「a」をメモします。
b〜eも同様にメモします。
要は 図1-4 と同じことをやるわけです。
すべてメモすると 図3-3 のようになりました。
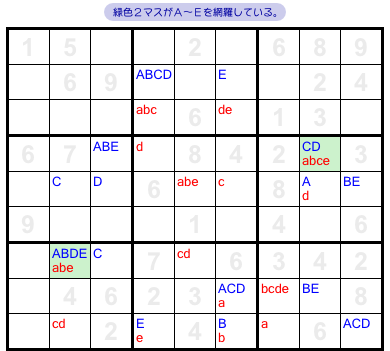
さて、メモをしたはいいものの……。
ここから先、何をすればいいんでしょう?
大文字小文字の両方を持つマスに注目しましょう。
例えば、緑色2マス(図3-4)。
この2マス全体を見ると、A〜Eがすべて現れていますね。
となると、こういうことが言えるんです。
- 緑色2マスのうち少なくとも1つには数字1が入る。
理由は簡単です。
数字1のパターンはA〜Eの全5種類だからですね。
その5種類のどれが採用されようとも、緑色マスのどちらかには必ず数字1が入ることになるんです。
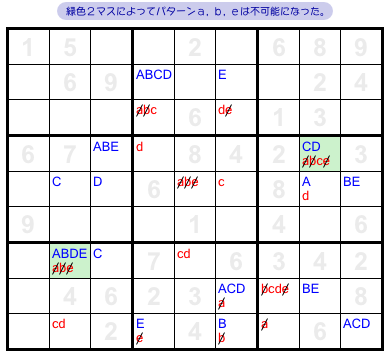
緑色2マスの少なくとも一方には数字1が入ります。
言い換えると、「緑色マス全部を数字9で埋め尽くす」ことは不可能になりました。
そうなると、数字9についてこんなことが判明するんです。
- パターンa, b, eはすべて却下される。
なんと!
5つあったパターンから3つも消え去り、cとdの2つしか残らなくなるんです。
数字9のパターンが減ってしまう!
なぜ却下されるんでしょう?
パターンa, b, eは緑色マス全部を数字9で埋め尽くす形をしています。
ところが、その「数字9で埋め尽くす」は不可能だ。
というわけで、パターンa, b, eが採用される可能性はもう完全に無いんです。
パターンa, b, eはもう考慮から外します。
盤面からa, b, eをすべて消しちゃいましょう。
数字9のパターンは5つから2つに減りましたね。
まさに数字1のパターンによって数字9のパターンが減らされてしまった恰好。
しかし、ここで数字9に新たな展開が起こるんです。
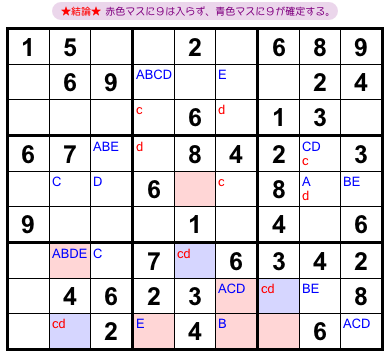
まずは赤色マス。
a, b, eがすべて消え去った今、赤色マスにメモa〜eは消滅してしまいました。
次に青色マス。
もともと青色マスにはcもdもメモされていましたが、今や数字9のパターンはc, dの2種類しかありません。
では、結論を発表しましょう。
こうなるんです。
- 赤色マスに数字9を入れられなくなる。
- 青色マスに数字9が確定する。
4.この解法、人間は使えません
ここからは余談です。
解法 Pattern Overlay Method の大変さについて、ちょいと話をしてみます。
いきなり言っちゃいますが、Pattern Overlay Method という解法は人間の手に負えるシロモノではありません。
それはそれは凄まじく手間がかかるからなんです。
ま、これはすぐに想像つきますよね。
なんたって、特定の数字の入り方を全パターン挙げるわけですもん。
空きマスが多ければ多いほど、パターンの数は膨れあがります。
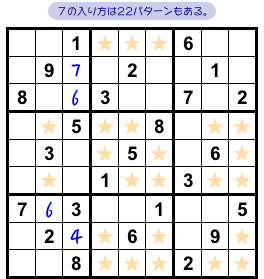
図4-1 は序盤も序盤、4マスだけ埋まっています。
この段階で数字7の入り得る場所は★の位置。
さて、この盤面で数字7の入れ方は何通りあるでしょう?
数えてみたら 22通りでした。
多すぎる😅
こりゃぁ人力で全パターン挙げるのはシンドい……どころか発狂してしまう!
Pattern Overlay Method がどれだけ手間のかかる解法か。
それが垣間見えますね。
百歩譲って、その22パターンから結果が1つでも見つかればマシかもしれない。
しかし、残念ながら何ひとつ見つかりませんでした。
無闇に Pattern Overlay Method を使っても、ただただ骨折り損で終わるばかり。

究極の場合を考えてみましょう。
完全にまっさらな盤面に数字Xを9つ入れてみる。
入れ方の一例は 図4-2 ですね。
果たして、数字Xの入れ方は全部で何通りあるんだろう?
答えは 46,656通りです。
46,656通り。
声も出ません😵
一応、9カ所のうち1カ所に数字Xが確定するだけで 46,656通りから 5,184通りに減るんだけれど、それでも数がバケモノじみてます。
9分の1に減ったというのに、それでも気が遠くなる😓
ラスボスが側近になったくらいの数かな。
でも、HP:5184 の側近に立ち向かえる勇者はこの世にいるんだろうか。
5184ターンも必要なんですが😅
基本的に Pattern Overlay Method は人間向きの解法ではありません。
特に、序盤で使おうなどと無謀なことは控えましょう。
ましてや、前セクション3みたいなことを人力でやろうなどとは夢にも思ってはいけません😅
ただ、セクション2のようにマス数がごく僅かだったなら手作業でもイケる。
だから、この解法を頭の片隅に入れておくのはアリかもしれません。
参考・参照
- Sudopedia ミラーサイト, 『Pattern Overlay Method』,
http://sudopedia.enjoysudoku.com/Pattern_Overlay_Method.html#Multi-Digit_Pattern_Elimination
更新履歴
- 2022. 2. 5.
- 新規公開。
- 2023. 3.31.
- ページ冒頭に難易度表記を追加。