【コラム】ルールには無駄がある !?

　ナンプレを解くにあたって大事なナンプレルール。
　なんと、そのルールに「多すぎる」という疑いがあるとかないとか !?
　ルールの個数についての話です。
　（難易度：★★★★）

１．１個ぐらい無くなっても……

　ナンプレのルール。
　何百何千と解いてきた皆さんには骨の髄まで染みわたっていることでしょう。
　そのルールについて、こ〜んなことを考えたことはありませんか？

ルール、ちょっと多すぎじゃない？

　「何言ってんだお前はｗ」とか言われそう😅
　でも、実は、ルールの個数について奇妙な事実が１つあるんです。
　その話をちょいとしてみたい。

図 1-1

　まずその前に、用語を定義しておきます。
　盤面の中にあるタテ列・ヨコ列・ブロック、これらを総称して house と呼びます。
　当然ですが、house には「数字１〜９を１個ずつ入れなければいけない」というルールがありますよね。
　当ページではそれを ミニルール と呼ぶことにします。

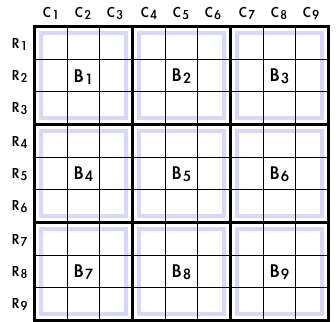
　図1-1、それぞれの house に記号を付けてみました。
　ヨコ列は R1～R9、タテ列は C1～C9、ブロックは B1～B9。
　この27個を使うと、ナンプレのルールはこう表現されます。

  • R1〜R9、C1〜C9、B1〜B9、この27個はすべてミニルールを守らなければならない。

　ナンプレのルールは一文で書かれていることが多いけれど、実際は27個のミニルールが存在しているわけです。

　27個。
　……ずいぶん多いよね😅

図 1-2

　実際、27個は本当に多すぎるんです。

　その理由を示すために、今、ちょいと変なことを考えてみましょう。
　27個の house のうち１個だけ、これを許可してみます。

  • R9 だけミニルールを破っても良いよ！

　R9 だけはどんなに数字が重複しようが何しようがお咎めなし！
　無法地帯にしちゃおう、というのです。

　ミニルールを27個から１個だけ減らし、26個のミニルールを守りながらナンプレ盤面を数字で埋め尽くしてみる。
　この時、一体どんなことが成り立つんでしょう？
　特に、R9 について何が言えるのか？

図 1-3

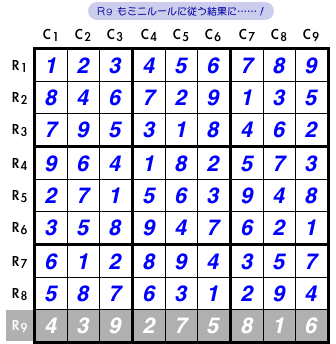
　実は、こんなことが言えるんです。

  • それでも R9 はミニルールに従うことになる。

　なんと！
　ミニルールを破ってもいいよと言われたのに、結局はミニルールを守ることになってしまう。
　ヨコ列 R9 の秩序は乱れないのです。

　もちろん、これは証明できます。
　どのタテ列もミニルールに従うから、タテ列 C1〜C9 に数字１は１個ずつ入る。
　だから、盤面全体に数字１は９個入ることになる。
　そのうちの８個は R1〜R8 に費やされるから（R1〜R8 もミニルールに従うので）、最後の数字１は R9 に入れるしかない。
　数字２〜９についても同じ理屈が成り立つから、R9 には数字１〜９が１個ずつ入ることになる。
　結局、R9 もミニルールに従う形になってしまう。
　こういうわけですね。

　R9 からミニルールを撤廃しても、ナンプレは必ず正しく完成する。
　この事実から一体何が推測できるのか？

　ルールには無駄がある。
　なんという驚きの結末だろうか。

２．ルールの過多を論じた論文がある

　まぁ、実を言うと、「ルールには無駄がある」という言い方は少し語弊があります。
　現実のナンプレを解く時はミニルール27個をすべて駆使するのだから、その意味では決して無駄ではありません。
　今回は、解く以外の視点でミニルールの多さを語ってみようというわけです。

　実は、ナンプレルールの過多について論じた論文が存在します。
　『Redundant Sudoku Rules』という論文。2012年に発表された物です。
　その論文の中で Googleグループ「rec.puzzles」に寄せられた投稿コメントを挙げていますが、もしかしたら、それが研究に着手したキッカケなのかもしれません。
　その投稿コメントには、軽い考察の後にこういう質問が書かれてありました。

what’s the minimum amount of checking that needs to be done to show that a completed 9x9 grid is valid?

　「９×９のナンプレ盤面が矛盾なく完成していることを示すためには、どのくらいのチェック量が最低必要ですか？」
　本来は、ナンプレが完成したかどうかを確かめるには27個の house をすべて調べなければいけません。
　しかし、「27個も調べる必要はない」ということは既に知られていて、「じゃぁ何個まで減らせるんだろう？」という疑問は当然生まれるわけですね。
　その疑問をこの論文が解決した。
　そういう次第です。

　その論文ではプログラミングを使って結論を導いていますが、そのために補題をいくつか導入しています。
　もちろんその補題には証明も描かれているわけですが、証明方法がビジュアルにほぼ全振りしていて非常に珍しい！
　それも紹介しつつ、当ページのテーマを語っていきます。

　ここでひとつ注意書き。
　当ページの内容は、Bart Demoen, Maria Garcia de la Banda による論文『Redundant Sudoku Rules』を基にしています。
　以降は、この論文を「原論文」と呼ぶことにします。
　原論文の内容を正しく解釈して話すことを心掛けていますが、誤訳や誤解釈をしている可能性はゼロとは言えません。
　また、論文内容を端折っている場合もあります。
　したがって、当ページの正確性について完全な保証はできません。
　正確な内容を知りたい方々は、当ページではなく原論文をご覧ください。
　原論文は学術記事サイト『arXiv』のこのページでダウンロード可能です。

３．盤面に巣くう灰色 house たち

　当ページの本題は「最低必要なチェック量はどれくらい？」です。
　これは「最低必要なミニルールは何個？」と同じです。
　逆に言うと「ミニルールを27個から最大何個撤廃できる？」と同じですね。
　原論文ではこの「ミニルールの撤廃」に注目し、これをビジュアルだけで表現するという画期的な手法をとりました。

図 3-1

　その手法はかなりシンプルです。
　まず、ブロックの境界線だけを描いて盤面を簡略化する。
　そして、ミニルールを定めていない house だけを灰色にする。
　たったこれだけ！

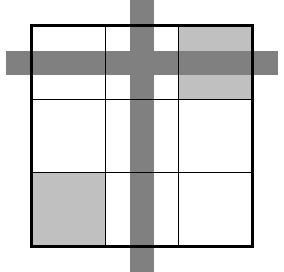
　図3-1 で具体例を１つ。
　この盤面は４個の house にミニルールが定められていません。
　R2, C5, B3, B7 の４個ですね。
　他の23個はミニルールに従います。

　もちろんですが、すべての house がミニルールに従っている場合は、灰色は１つもありません。
　つまり、盤面は真っ白です。

　ここで注意をひとつ。
　灰色の house は「必ずミニルールを破っている」という意味ではありません。
　「ミニルールを破っても良い」という意味であり、実際に破っているか否かは不明です。
　誤解しやすいので注意が必要です。

図 3-2

　そういえば、セクション１では一例を紹介しましたっけ。
　結果はこうでした。

  • R9 にミニルールが定められていなくても、結局 R9 はミニルールに従うことになる。

　この論述は 図3-2 の形で表現できます。
　あのセクションで長々と解説したことが、たったの１文字も使わずにこ〜んなにシンプルに表現できちゃう！

　図3-2 からわかる通り、「ミニルールに従うことになる」は「灰色を消せる」とまったく同じです。
　そして、すべての灰色 house を消して盤面を真っ白にできた時、「灰色だった house のミニルールは無駄」とわかるわけですね。
　ということは、消した灰色 house の個数が重要になってくる。
　セクション２で挙げた疑問は次のように言い換えられるんです。

真っ白にすることが可能な盤面、灰色 house を最大何個持てますか？

　その個数が結論を導いてくれます。
　もし仮に「最大６個持てる」と判明すれば、「最低必要なミニルールは21個」という結論になるんです。

　さぁ、もぅ方針は見えた！
　いかに灰色 house を論理的に消していくかが重要だ！
　でも……、どうやって灰色 house を消していくんでしょう？

４．灰色 house 全滅大作戦！

　どうやって灰色 house を消せばいいのか？
　実は、心強い武器が２つあるんです。

図 4-1

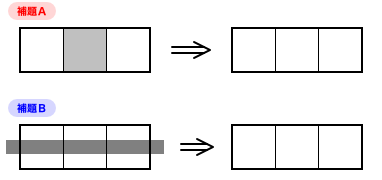
　その武器とは、図4-1 の２つの補題です。
　この２つは見た目が異なりますが、論旨は同じです。

  • R1 R2 R3 B1 B2 B3 のうち５つがミニルールに従っていれば、残りの１つも必ずミニルールに従う。

　補題Ａは B2 だけが灰色。
　補題Ｂは R2 だけが灰色。
　どちらも消える運命にある、というのがこの補題の主張です。

　補題の証明は簡単です。
　補題Ａの場合、R1 R2 R3 はミニルールに従うから、この３×９マス領域には数字１が３個入る。
　そのうちの２個は B1 と B3 に費やされ、最後の数字１は B2 に入れるしかない。
　数字２〜９についても同じ理屈が成り立つから、結局、B2 には数字１〜９が１個ずつ入ることになります。
　補題Ｂも同様に証明できます。

　この３×９領域、chute という名前が付いています。
　縦長と横長の２種類あります。
　以降はこの名前で呼ぶことにしましょう。
　補題Ａ, Ｂは chute から灰色 house を除去するために使う物です。

図 4-2

　全滅成功の一例を挙げましょう。
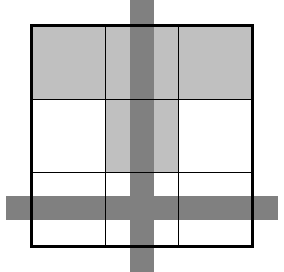
　図4-2 です。

  • 灰色 house は R8 C5 B1 B2 B3 B5 の６つ。

　さすがに６つもあると、盤面が灰色だらけ。
　こんな状態だと、全滅なんて不可能そうに見えますよね。
　上端の chute なんて完全に灰色だけど、大丈夫なんかいな……？

　もちろん心配はご無用！
　補題たちが綺麗サッパリ解決してくれます。

　では、全滅させましょう！
　次の手順でＯＫです。

　青色枠の chute に補題をどんどん適用しましょう！

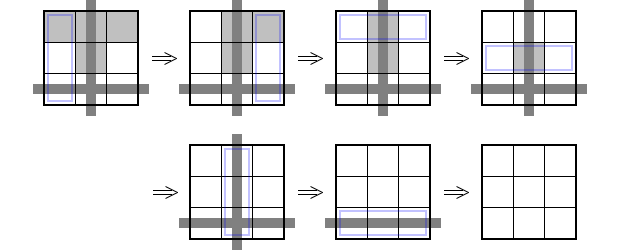
　このように２つの補題が大活躍！
　灰色 house がジワジワと１個ずつ消えていく。
　あんなに灰色だらけだった盤面がめでたく真っ白に😊
　灰色 house 全滅作戦、大成功！

　図4-2 からは、途中経過ながら１つの結果が出ましたね。

　おぉ〜！　２割以上も減らせたぞ！
　これは、まだまだ減らすことができるかもしれない？

５．そして結論へ……

　もちろん、成功例だけでは結論は出せません。
　失敗例も知らないと、灰色個数の上限は見えてきません。
　全滅不可能な盤面にも目を向けてみましょう。

図 5-1

　例えば、図5-1。

  • 灰色 house は C1 C3 の２つ。

　この盤面、実はどちらの灰色も消せません。
　左端の chute にしか灰色がなく、しかも、そこには灰色が２カ所あるからです。
　補題の使いどころが１つもない😞

　試しにこの盤面を数字で埋めてみると、矛盾を持つ盤面を作れます。
　C1, C3 以外はすべてミニルールを守っているのに、灰色 house ではおかしなことが起きている。
　この灰色配置では、ナンプレが必ず正しく完成できるとは断言できないんですね。

　原論文チームは、灰色６個の盤面を 全滅可能/不可能 の２種類に分類するという作業を行いました。
　図5-1 はその過程で見つかった物です。おそらく、灰色を４個消した時点で全滅不可能だと判明したのでしょう。
　灰色６個の分類が終わると、それを基に今度は灰色７個の盤面に着手。
　そこでついに大きな結果にたどり着きます。

灰色 house を７個持つ盤面はすべて全滅不可能だった。

　これで最終結論は得られました。
　次の通りです。

　最後に。
　この話題の本質的な部分、それは２つの補題と 図5-1 の２つです。
　chute の中にある灰色 house の個数、これがすべてを物語っていました。

　原論文チームは、図5-1 を含め全滅不可能な盤面を見つけていました。
　灰色７個以下の物だと次の８種類です。

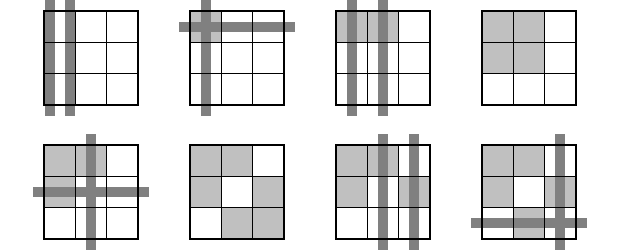
　この８つの盤面を見ると、灰色 house を１個だけ持っている chute は１つもありません。
　だから、灰色除去の最中にこれらの状況になると補題Ａ, Ｂは完全に出番を失い、全滅作戦が立ち往生してしまうわけです。

　原論文によると、灰色 house を７個持つ盤面を調査すると、どの盤面もこの８種類のどれかに帰着したそうです。
　そのため、すべての盤面で灰色全滅作戦は失敗となり、「灰色 house の上限は６個」だと判明するんですね。

参考・参照

更新履歴