1.Fish が退化する !?
まずは、Sashimi 型 Fish の大きな特徴である「Fish の退化」について解説します。
すでにご存じの方々はセクション2に進んじゃってください😊
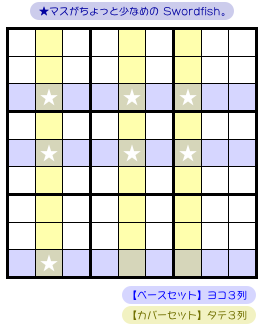
Swordfish を例に話を進めていきましょう。
図1-1、Fish は以下の状況になっています。
- 青色ヨコ3列において、数字1の入り得るマスは★のみ。
- そして、その★マスすべてを黄色タテ3列で覆い尽くせた!
青色3列をベースセット、黄色3列をカバーセットと呼びました。
さて。
図1-1 の盤面、★の個数は9個よりも少ないですね。
しかし、ベースセット/カバーセットのページで補足説明した通り、これは正当な Swordfish です。
さて。
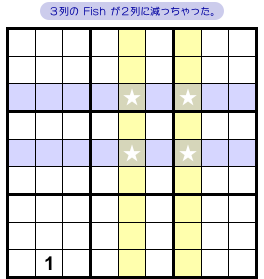
★の配置をよく見ると……、一番下のヨコ列には★が1個しかありません。
あれ? その列に数字1が確定しちゃうじゃん!
というわけで、その★マスに数字1を入れましょう。
すると、他の青色列では数字1の入り得るマスが2個ずつに減りました。
なんと!
Swordfish が X-Wing に変わってもぅた!
★の配置によっては、一部のマスに数字1が確定して列数が減ってしまう。
このように、元の Fish から列数が減ってしまい、小サイズの Fish に姿を変えてしまうことがあるんです。
これを Fish が退化する と言います。
退化のパターンはいくつかあります。
簡単なのは、図1-2 みたいに1サイズ小さくなるというパターンですね。
他には、Jellyfish が2個の X-Wing に分裂したりします。4列のように見えて実は2列×2だったという……。
極端な場合だと、どの列にも次々と数字1が確定してしまって Fish 自体が消滅! ……なんて可能性もあったり。
退化を通り越しちゃう😅
このページでは、1マスにだけ数字1が確定して Fish が1サイズ退化する場合のみを扱うことにします。
退化のパターンはいっぱいあるけれど、複雑なパターンはここでは扱いません。
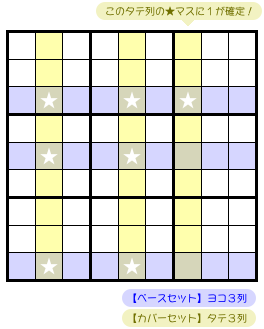
もうひとつ、Swordfish の例を紹介しましょう。
今度は、カバーセットのとある黄色列には★が1個しかありません。
実は、この Fish も退化するんです。
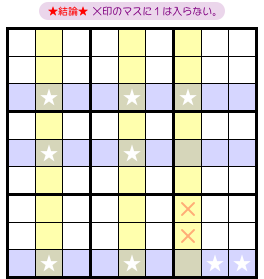
なぜなら、Fish にはこういう結論があったからです。
- カバーセットにおいて、★以外のすべてのマスに1を入れられなくなる。
つまり、図1-3 の黄色マスに数字1は入れられない。
★以外の黄色マス、全滅!
……だったわけですね。
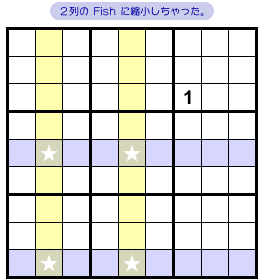
というわけで、その黄色列では数字1は★マスに入るしかない。
すると、他の2列に影響が出て、1の入り得るマスが2個ずつに減っちゃいます。
Fish は2行2列の X-Wing に退化するんですね。
Sashimi 型の Fish 系解法では、この Fish の退化が関わっています。
それを軽く踏まえながら、以降のセクションをご覧ください。
2.Sashimi Fish とは何ぞや?
このセクションでは、Sashimi Fish を説明します。
前セクションで説明した「Fish の退化」も現れます。
2-1.こういう Fish です
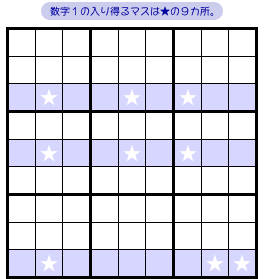
図2-1 を見てみましょう。
青色ヨコ3列において数字1の入り得るマスを探した時、★の9カ所しかなかったとします。
これら9マスは……整列していると言っていいんだろうか?
んもぅ明らかに列を乱しまくってんのが約2名😅
それでもまぁ、3行3列の整列っぽくは見える。
じゃぁ、タテ3列で覆ってみましょうか。
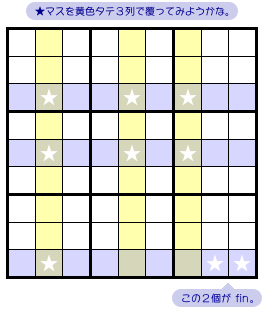
やっぱり★が2個漏れちゃいました😅(図2-2 右下)
そりゃ漏れるよねー😅
青色ベースセットの★マスを黄色カバーセットで覆いきれませんでした。
あぁ残念😞
というわけで、前図2-1 からはこういう状況になりました。
- 青色ヨコ3列において、数字1の入り得るマスは★のみだった。
- そして、その★マスを黄色タテ3列で覆ってみた。
- すると、★マスが2個漏れてしまった。
この漏れてしまった★マスのことを fin と呼びます。
fin は「ひれ」という意味です。
"Fish" 系の解法らしく、魚の「ひれ」ですね。
Exofin のページでは exofin を紹介していますが、それとまったく同じものです。
このページでは、exofin ではなく fin と呼ぶことにしましょう。
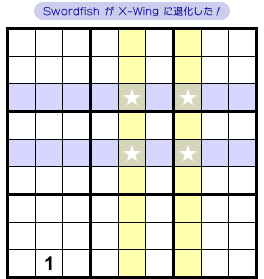
さて、この Fish にはさらに大きな特徴があります。
前図2-2 の Fish、どの青色列を見ても★マスは2つ以上ありますね。
だから、直ちに数字1が確定するわけではありません。
ただ、仮に fin をすべて取り除いたとしたらどうなるでしょう?
取り除いた直後はただの Swordfish になります。
だけど、その Swordfish をよく見ると…… おぉ、一番下のヨコ列、★が1個しかないじゃないの!
そうなると、その★マスに数字1が確定する。
そして、Swordfish が X-Wing に変わってしまう(図2-3)。
なんと、Fish が退化しよった!
こういうふうに、fin を持つ Fish のうち、その fin をすべて取り除くと退化してしまうものがあります。
このような Fish のことを Sashimi Fish と言います。
前図2-2 は Sashimi Swordfish ですね。
ここで、ひとつ白状します。
実は、Sashimi Fish と Finned Fish には本質的な違いはありません。
なぜなら、両者とも Fish の形は本質的に同じだからです。
どちらも「★マスのタテヨコ整列に fin がくっついたもの」なんです。
じゃぁ、何が違うのか。
それは、仮に fin を全消ししたら Fish が退化するのか、それとも退化しないのか。
それだけ😅
前者を Sashimi、後者を Finned と区別しているだけなんです。
というわけで、Finned Fish の解法をご存じの方々はここから先を読む必要はありません。
だって、論理展開も結論もまったく同じなんだもの😓
でも、それじゃぁこのページの意味がないから、一応 Sashimi Fish から得られる結論を以下で解説していくことにしましょう。
2-2.どういう結論になるの?
さて、Sashimi Fish からはどういう結論が得られるんでしょう?
それを解説していきます。
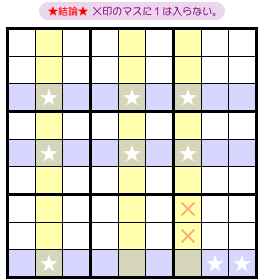
実は、単に fin が散らばっているだけだと何の結論も得られません。
しかし、すべての fin と同じブロックに属している黄色マスがある場合、次の結論が得られるんです。
- カバーセット内部の★以外のマスのうち、すべての fin と同じブロックに属しているマスがある。そのマスに数字1は入らない。
図2-4 だと、×印の2マスが該当します。
この2マスはカバーセット内部にあり、かつ、すべての fin と同じブロックに属しています。
この2マスに数字1は入らなくなるんですね。
なぜこういう結論になるんでしょう?
それを解説しましょう。
とりあえず言えるのは、次のどちらかが必ず成り立つということです。
- どれかの fin に数字1が入る。
- どの fin にも数字1は入らない。
この両者についてそれぞれ論理展開していきましょう。
まずは前者。
これは簡単です。
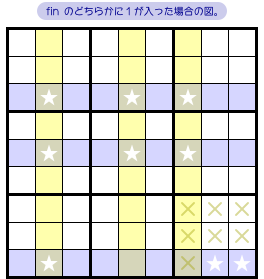
fin のどちらに数字1が入ろうとも、同じブロック全体に数字1が入らなくなります(図2-5 ×印)。
次に後者。
この場合は、fin がすべてなくなります。
つまり、ただの Fish に様変わり!
様変わりした時点では、その Fish は Swordfish です。
しかし、一番下の青色ヨコ列では数字1は★マスにしか入れられなくなってますね。そのマスに1を確定させましょう。
すると、Swordfish は X-Wing に退化しちゃいますね。
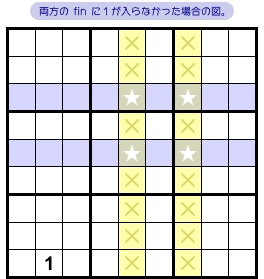
ということで、最終的には★以外のすべての黄色マスに数字1が入らなくなります。
退化はしたけど、★以外の黄色マス、全滅!(図2-6 ×印)。
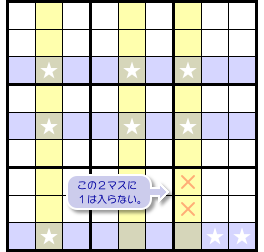
図2-5 と 図2-6、両者のうち一方が成り立ちます。
2つの図を見比べてみると……おぉ、共通して×印のついているマスがありますね!
そのマスに数字1は入らないということが言えるんです。
具体的には 図2-7 の2マスです。
図2-4 の結論通りになりましたね😄
2-3.もうひとつのパターン
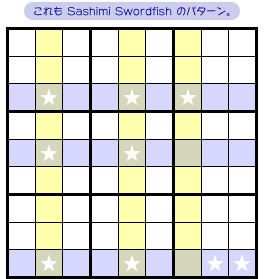
もうひとつのパターンを紹介しましょう。
今度は、ある黄色タテ列に★マスが1個しかありません。
そして、その★マスと fin はタテに並んでいませんが、両者の属するブロックはタテに並んでいます。
これも Sashimi Fish(Sashimi Swordfish)です。
実際、右下隅の fin をすべて取り除くと、右側黄色列の★マスに数字1が確定して X-Wing に退化しちゃいますね。
この場合も結論は同じです。
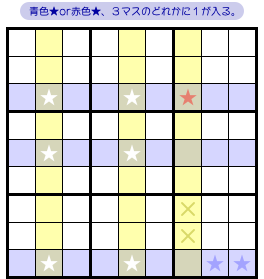
- カバーセット内部の★以外のマスのうち、すべての fin と同じブロックに属しているマスがある。そのマスに数字1は入らない。
図2-9 だと、×印の2マスが該当します。
この2マスはカバーセット内部にあり、かつ、すべての fin と同じブロックに属しています。
この2マスに数字1は入らなくなるんですね。
理由は 図2-5~図2-7 で示したのと同様です。
次の両者をそれぞれ論理展開していけばOKです。
- どれかの fin に数字1が入る。
- どの fin にも数字1は入らない。
前者の場合は、青色★マスのどちらかに数字1が入る。
後者の場合は、右端の黄色列では数字1は赤色★マスに入れるしかない(ついでに Fish が退化する)。
結局、青色・赤色★マスのどれかには必ず数字1が入るから、×印の2マスに数字1を入れられないというわけです。
図2-9 の結論通りになりましたね😄
3.複雑な Sashimi Fish
セクション2で解説した Sashimi Fish はそれほど難しい概念ではありません。
しかし、Fish には Franken Fish や Mutant Fish もありましたね。
もちろん、それらにも Sashimi があるんです。
このセクションでは、そういう複雑な Sashimi Fish を紹介します。
……とその前に、house という用語を紹介しましょう。
house とは、タテ列・ヨコ列・ブロックの総称です。
これは英語のナンプレ解説サイトでも使われている用語で、英語の解説を読むと house というワードがやたらと現れます。
以降では、house はタテ列・ヨコ列・ブロックのどれかを指すものだと考えちゃってください。
3-1.Sashimi Franken Fish
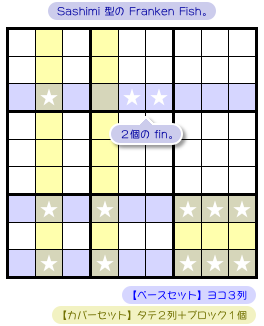
さて、図3-1 の盤面、こういう状況になっています。
- 青色ヨコ3列において、数字1の入り得るマスは★のみだった。
- そして、その★マスを3個の黄色 house で覆ってみた。
- すると、★マスが2個漏れてしまった。
ベースセットは青色のヨコ3列です。
カバーセットは黄色のタテ2列&ブロック1個です。
漏れた★マス2個が fin です。
そして、fin をすべて取り除くと Fish が退化することを確認してみてください。
一番上の青色ヨコ列に数字1が確定して、ベースセットもカバーセットも house が2個ずつに減っちゃいます。
ということで、図3-1 は Sashimi 型の Franken Swordfish ですね。
これを Sashimi Franken Swordfish と言います。
名前が長ぇ😓
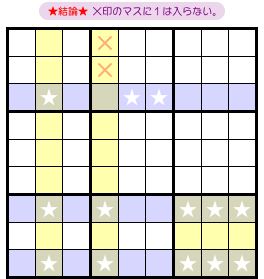
セクション2-2では「すべての fin と同じブロックに属している黄色マスがある場合、結論が得られる」と説明しました。
- カバーセット内部の★以外のマスのうち、すべての fin と同じブロックに属しているマスがある。そのマスに数字1は入らない。
これは一般的な表現ではありません。
ここでは、もっと一般的な言い方をしましょう。
こうなります。
- カバーセット内部の★以外のマスのうち、どの fin とも house を共有しているマスがある。そのマスに数字1は入らない。
図3-2 だと×印の2マスが該当します。
その2マスはどの fin ともブロックを共有しています。
この2マスに数字1は入らないというわけです。
なんだかこれだけだと「言い方を変えただけじゃないの?」と言われそう😅
実は、fin が異なるブロックに属している場合があるんです。
どの fin とも house を共有しているマス、これがカバーセット内部に存在するかどうかなんですね。
文字だとピンとこないかもしれない😓
セクション3-2で具体例を挙げて説明しましょう。
3-2.Sashimi Mutant Fish
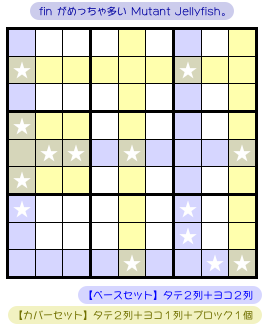
図3-3 の盤面はこういう状況になっています。
- 4個の青色 house において、数字1の入り得るマスは★のみだった。
- そして、その★マスを4個の黄色 house で覆ってみた。
- すると、★マスが4個漏れてしまった。
ベースセットは青色のタテ2列&ヨコ2列です。
カバーセットは黄色のタテ2列&ヨコ1列&ブロック1個です。
漏れた★マス4個が fin です。どれも盤面下部にあります。
図3-3 は fin の付いた Mutant Jellyfish ですね。
4個の fin がすべて同じブロックに属しているというわけではありません。
1個だけ違いますもんね。
そこにも少し注意してください。
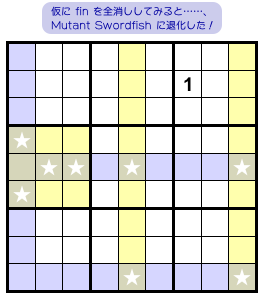
図3-3 の Fish、パッと見では Sashimi には見えなさそう。
でも、これは Sashimi なんです。
ちょいと試しに fin をすべて取り除いてみましょう。
すると、右側の青色タテ列では★マスが1個しかなくなりますね。そこに数字1が確定して…… Mutant Swordfish に退化しちゃいました。
というわけで、これは正真正銘の Sashimi Mutant Jellyfish です。
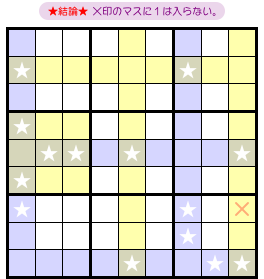
図3-2 でも述べましたが、結論はこうなります。
- カバーセット内部の★以外のマスのうち、どの fin とも house を共有しているマスがある。そのマスに数字1は入らない。
図3-5 だと×印の1マスが該当します。
そのマスはカバーセット内部にあり、左端の fin とはヨコ列を共有し、残り3つの fin とはブロックを共有しています。
そのマスに数字1は入らないというわけです。
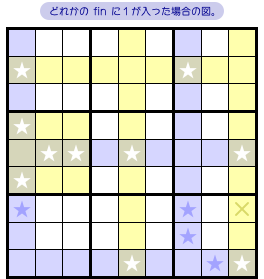
セクション2-2と同じ説明になっちゃいますが、なぜ 図3-5 の結論が得られるのかを解説しましょう。
とりあえず言えるのは、次のどちらかが必ず成り立つということです。
- どれかの fin に数字1が入る。
- どの fin にも数字1は入らない。
この両者についてそれぞれ論理展開していきましょう。
まずは前者。
fin は4つありますね。青色の★です(図3-6)。
fin の位置関係を見てみると、どの fin とも house を共有しているマスがカバーセット内部に存在しています。×印のマスです。
×印マスと fin の位置関係により、どの fin に数字1が入ろうとも×印マスに数字1は入りません。
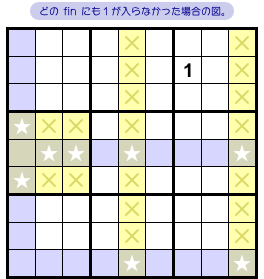
次に後者。
この場合は、fin がすべてなくなります。
つまり、ただの Mutant Jellyfish に様変わり!
さらに退化して Mutant Swordfish にもう一度様変わり!
ということで、★以外のすべての黄色マスに数字1が入らなくなります。
★以外の黄色マス、全滅!(図3-7 ×印)
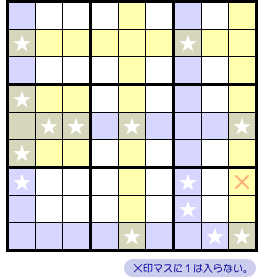
図3-6 と 図3-7、両者のうち片方が成り立ちます。
2つの図を見比べてみると……おぉ、共通して×印のついているマスがありますね!
そのマスに数字1は入らないということが言えるんです。
具体的には 図3-8 の1マスです。
図3-5 の結論通りになりましたね😄
更新履歴
- 2022. 2. 5.
- 新規公開。
- 2023. 3.31.
- ページ冒頭に難易度表記を追加。