1.双対とクラスター
Simple Colors の舞台、それは「クラスター」です。
1種類の候補数字nが「双対」でつながっている世界。
その世界は二大勢力に分かれていて、そのどちらに数字nが入るのかが一番の関心事。
なんだか不思議な世界です。
このセクションでは、双対とクラスターを解説していきます。
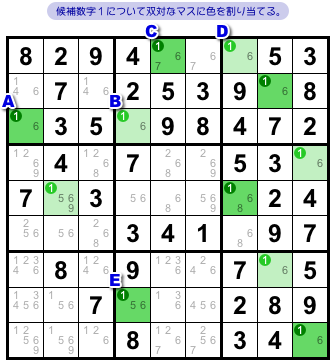
ある列やブロックにおいて、数字nの入り得るマスが2つしかないとします。この時、その2マスは 数字nについて双対である と言うことにしましょう。あるいは、単に 双対である と言うことにします。
例えば、図1-1 において候補数字1に注目すると、2マスA, Bは双対です。B, Cも双対ですね。C, DもB, Eも双対です。
ここでは、双対である2マスに色付けをします。
その際、次のルールに従って2色を割り当てていきます。
- 双対である2マスには異なる色を割り当てる。
- ある1マスが複数のマスと同時に双対である場合、相手のマスすべてに同じ色を割り当てる。
候補数字1に対して a. b. を適用してできたのが 図1-1 です。
a. の例としては、双対な2マスA, Bには異なる色が割り当てられています。双対な2マスB, Cも色が異なります。他も同様です。
b. の例としては、マスBと双対な3マスA, C, Eにはどれも同じ色が割り当てられています。マスCと双対な2マスB, Dも同じ色が割り当てられています。
なぜ、こういうルールで2色を割り当てるんでしょう?
それは、双対である場合、次の2つが必ず同時に成り立つからです。
- 一方のマスに数字1が入る。
- 他方のマスに数字1は入らない。
この「2つが必ず同時に成り立つ」というのがミソで、2色を割り当てることで 一方/他方 を可視化させるというわけです。
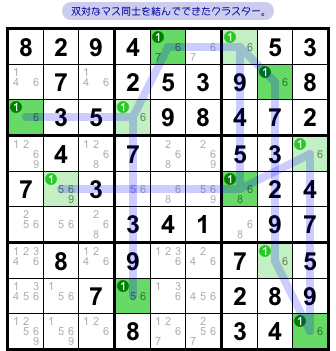
さて、双対である2マス同士を線で結んでみると、図1-2 のようにひとつながりの図形ができあがります。
これを クラスター と呼びます。
図1-2 では、数字1について緑色&薄緑色・全11個のマスからなるクラスターができました。
ちなみに、クラスターには「房」「群れ」といった意味があります。
海外のサイトでも cluster という用語を使ったりしています。
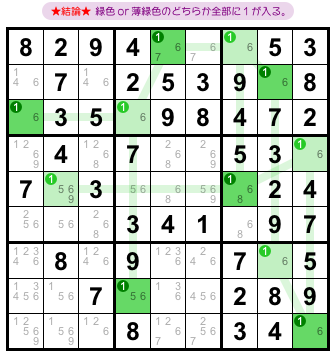
さて、前図1-2 のクラスター、何のために作ったのか?
こういう結論を得るためです。
- どちらか一方の色付きマス全部に数字1が入る。
具体的に言うと、次のどちらかが必ず成り立つということです。
- 緑色マス全部に数字1が入る。
- 薄緑色マス全部に数字1が入る。
なぜ「全部」なのかというと、緑色マスと薄緑色マスは双対の関係にあるからです。
クラスター上のとある1マスに数字1が入るか否かが判明した時、双対の関係によって他のすべてのマスも数字1が入るか否かが次々と波及していきます。
そして、ものの見事に色分けした通りに「1が入る/1が入らない」に二分されるという結果になるんです。
数字1が入るのは緑色? それとも薄緑色?
この2択に帰着できる。
これが色付けの最大の意味なんです。
Simple Colors では、1個のクラスターを使って解き進めます。
例を2つ挙げて解説していきましょう。
2.こんな手筋があるよ!・その1 (Color Trap)
まずは1つめの手筋です。
Color Trap という名前が付いています。
例として、前セクションの盤面をそのまま流用しちゃいます。
手抜きとか言わないで😅
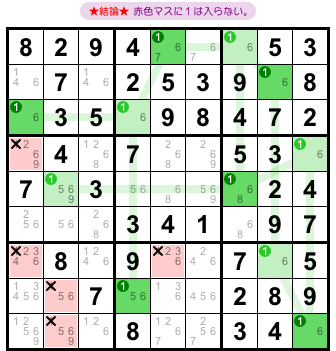
図1-3 からは、こういう結論が得られます。
- 緑色マス・薄緑色マスの両方と列やブロックを共有しているマスがある場合、そのマスに数字1は入らない。
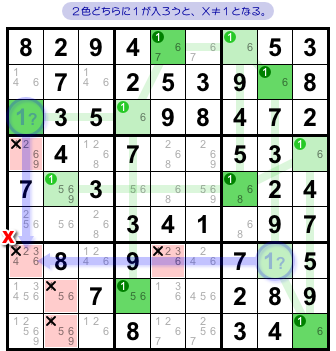
図2-1 だと、赤色のマスが該当します。
この5マスに数字1を入れられなくなるんです。
なぜ、こういう結論になるんでしょう?
それを解説しましょう。
前セクションで述べた結論が効いてくるんです。
次のどちらかが必ず成り立つんでしたね。
- 緑色マス全部に数字1が入る。
- 薄緑色マス全部に数字1が入る。
となると、両方の色と列やブロックを共有しているマスに影響が出るんです。
例えば、左端のマスX。
真上には緑色マスがあり、右には薄緑色マスがありますね。
その2マスの片方に必ず数字1が入るわけだから、マスXには1を入れられない。
こういうわけなんです。
他のマスも同様です。
結局、赤色5マスの候補数字1がすべて除去されるんですね。
前図2-2 の後も解き進められるので、ちょいと解説。
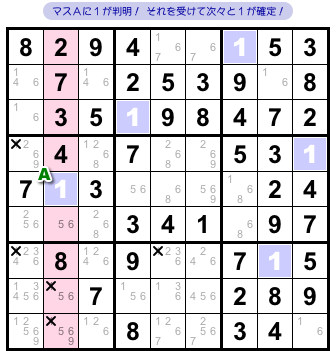
図2-2 では、5マスに数字1を入れられなくなりました。
それを踏まえてピンク色のタテ列に注目すると、なんと、数字1の入れられるマスはAしかない!
というわけで、マスAに1が確定しました。
しかし、それだけでは終わらない!
マスAはクラスターの薄緑色マスでしたよね。
ということは、薄緑色のマス全部に数字1が確定してしまうのです。
まさに一蓮托生ですね。
数字1の入る運命を共にする。
これが Simple Colors の大きな威力なんです。
3.こんな手筋があるよ!・その2 (Color Wrap)
2つめの手筋です。こういう解き方もあるんです。
Color Wrap という名前が付いています。
このセクションでは、青色と水色でクラスターを色分けします。
ここでは、前セクションとは違う盤面で説明しましょう。
今度は青色&水色の2色を使ってクラスターを作っていきます。
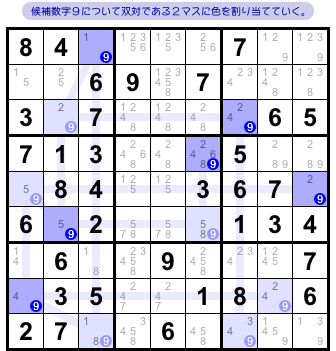
候補数字9に注目すると、クラスターは 図3-1 の通りになりました。
青色&水色・全12個のマスからなるクラスターです。
では、このクラスターから何が言えるんでしょう?
こういう結論になるんです。
- ある列やブロックが同じ色のマスを2個以上含んでいる場合、その色のマスすべてに数字9は入らない。
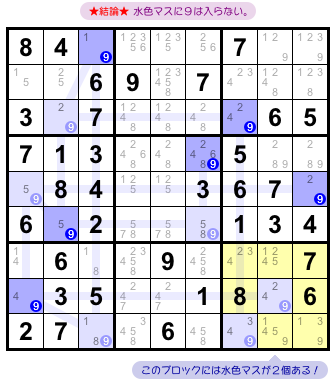
図3-2 だと、水色のマスが該当します。
黄色ブロックを見てみると、その中に水色マスが2つありますね。
そのため、すべての水色マスに数字9を入れられなくなるんです。
なぜ、こういう結論になるんでしょう?
それは簡単です。
水色マス全部に数字9を入れちゃうと……ご想像通りの結末に😵
破綻しちゃいますもんね。
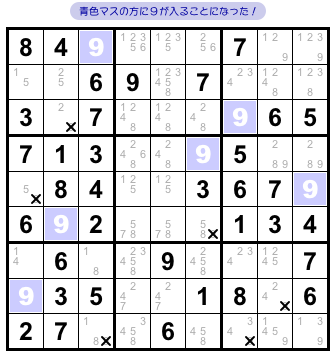
水色マスに数字9を入れてはダメ。
となれば、残った青色の方に数字9が入る。
こういうことになりました😊
こういうふうに、不合理の視点で解き進められることもあるんですね。