【解法】Sue De Coq

　Sue De Coq は１列とブロック１個に含まれるマスを使った解法で、候補数字の分布に特徴があります。
　（難易度：★★★★）

１．どういう解法？

　解法 Sue De Coq を使う際は、列とブロックの２つに注目します。
　そして、両者の交差部分にも注目します。
　そのため、列とブロックが交差していなければ Sue De Coq は使えません。
　このセクションでは、例を２つ挙げて説明します。

1-1．基本パターン

図 1-1

　図1-1 には青色ヨコ列と黄色ブロックがあります。
　そして、両者が交差してできた緑色３マスもありますね。
　このうち、緑色領域・青色の１マス・黄色の１マス、合計５マスに注目します。それぞれＡ, Ｂ, Ｃとしておきましょう。
　この５マスには次の特徴があります。

  • ５マスが持つ候補数字は 2, 3, 4, 7, 9 の全５種類。
  • 領域Ａには５種類の候補数字がすべて存在する。
  • マスＢの候補数字は２と７。マスＣの候補数字は３と４。どちらも上記の全５種類のうちの２種類である。
  • ２マスＢ, Ｃに共通する候補数字はない。

　図1-1 でビジュアル的に理解しちゃった方が早いかも😊
　領域Ａの候補数字５種類のうち２種類ずつがＢとＣに振り分けられている、という感じです。

　こういう状況の時、Sue De Coq が使えるんです。

図 1-2

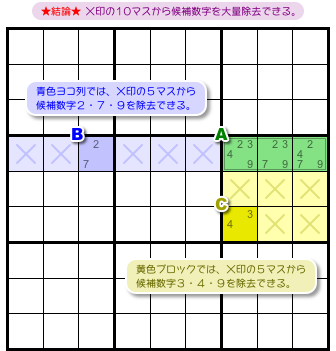
　さて、前図1-1 からはどういう結論が得られるんでしょう？
　こうなります。

  1. 青色ヨコ列において、ＡとＢ以外のすべてのマスから候補数字２と７を除去できる。
  2. 黄色ブロックにおいて、ＡとＣ以外のすべてのマスから候補数字３と４を除去できる。
  3. 青色ヨコ列と黄色ブロックにおいて、Ａ, Ｂ, Ｃ以外のすべてのマスから候補数字９を除去できる。

　図1-2 だと、10マスが該当します。
　a. に該当するのは青色×印のマスです。その５マスから候補数字２と７を除去できます。
　b. に該当するのは黄色×印のマスです。その５マスから候補数字３と４を除去できます。
　c. に該当するのはすべての×印マスです。その10マスから候補数字９を除去できます。

　ものすごい大量除去が起きますね！
　なぜ、こういう結論になるんだろう？
　それを説明しましょう。

　あ、説明の前に。
　結論 a. にある「候補数字２と７」はちょうどマスＢの候補数字と同じです。
　結論 b. にある「候補数字３と４」はちょうどマスＣの候補数字と同じです。
　結論 c. にある「候補数字９」は領域Ａにのみ存在する候補数字です。
　それを踏まえて 図1-2 を見ると理解しやすいかもしれません。

図 1-3

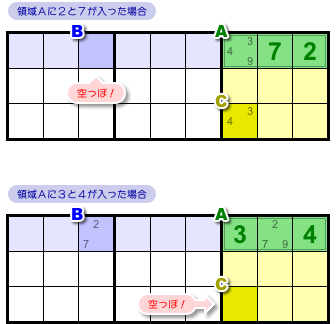
　まず、領域Ａに入る数字をちょっと検討してみましょう。

　もしＡのどこかに数字２も７も入ったとすると、マスＢに入れる数字がなくなっちゃいます。これはダメ。
　２と７のうち少なくとも一方は領域Ａに入れてはいけません。

　また、もしＡのどこかに数字３も４も入ったとすると、マスＣに入れる数字がなくなっちゃいます。これもダメ。
　３と４のうち少なくとも一方は領域Ａに入れてはいけません。

　領域Ａには候補数字が全５種類ありますね。マスより２個多い。
　だから、その中の２種類は領域Ａに入れてはいけない。
　そう考えると、次の a. b. c. が領域Ａの３マスにそれぞれ入ります。

  1. 数字２と７のどちらか。
  2. 数字３と４のどちらか。
  3. 数字９。

　果たして、この a. b. c. がどういう結果を生むんでしょう？

図 1-4

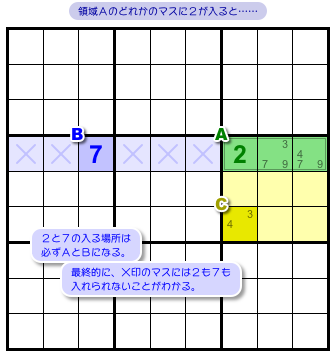
　まず、「a. 数字２と７のどちらか」を考えてみます。

　領域Ａのどこかに２が入ったとすると、それに連動してマスＢに７が確定します。
　ＡとＢの２カ所に２と７がそれぞれ収まるんですね（図1-4）。

　逆も同様です。Ａに７が入るとＢに２が確定する。
　この場合も、ＡとＢの２カ所に２と７が収まります。

あれ？　もしかして……
数字２と７って、ＡとＢにしか入らないんじゃない？

　そうなんです。
　青色ヨコ列において、数字２と７の入る場所はＡとＢに限定されてしまうんです。
　だから、他のマスには２も７も入れることはできなくなりました（図1-4 ×印）。

　これが 図1-2 の結論 a. です。

図 1-5

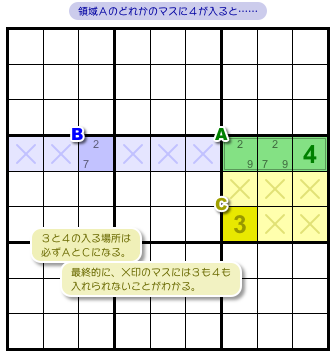
　「b. 数字３と４のどちらか」も理屈はまったく同じです。
　領域Ａのどこかに３が入ればマスＣに４が確定する。
　逆もしかり（図1-5）。
　だから、黄色ブロックにおいて、数字３と４の入る場所はＡとＣの２カ所に限定される。
　他のマスには３も４も入らないんです（図1-5 黄色×印）。
　図1-2 の結論 b. ですね。

　最後は「c. 数字９」です。
　これは、領域Ａのどこかに必ず９が入るということを考えれば、10個の×印マスに９が入らないことはすぐにわかります。
　図1-2 の結論 c. です。

　図1-2 の結論通りになりましたね😊
　これが Sue De Coq なんです。

1-2．こういうパターンもある

　上記では緑色領域は３マスでしたが、２マスに減っていてもかまいません。
　そのパターンについても軽く説明しましょう。

図 1-6

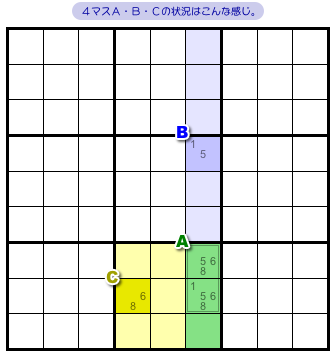
　図1-6 には青色タテ列と黄色ブロックがあり、両者が交差してできた緑色領域もありますね。
　今回は、緑色領域は２マスにだけ注目します。
　緑色２マスの領域をＡ、青色の１マスをＢ、黄色の１マスをＣとしておきます。
　この４マスには次の特徴があります。

  • ４マスが持つ候補数字は１, ５, ６, ８の全４種類。
  • 領域Ａには４種類の候補数字がすべて存在する。
  • マスＢの候補数字は１と５。マスＣの候補数字は６と８。どちらも上記の全４種類のうちの２種類である。
  • ２マスＢ, Ｃに共通する候補数字はない。

　図1-6 でビジュアル的に理解しちゃいましょ〜😊

図 1-7

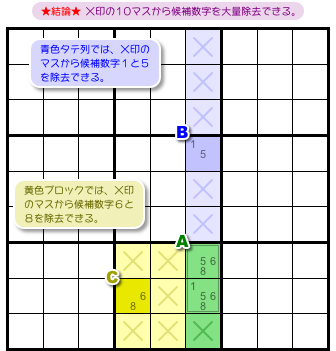
　結論はこうなります。

  1. 青色タテ列において、ＡとＢ以外のすべてのマスから候補数字１と５（マスＢの候補数字）を除去できる。
  2. 黄色ブロックにおいて、ＡとＣ以外のすべてのマスから候補数字６と８（マスＣの候補数字）を除去できる。

　図1-7 だと、10マスが該当します。
　a. に該当するのは青色×印のマスです（緑色マスの×印も含む）。その６マスから候補数字１と５を除去できます。
　b. に該当するのは黄色×印のマスです（緑色マスの×印も含む）。その６マスから候補数字６と８を除去できます。

　なぜこういう結論になるのかを簡単に説明しましょう。

図 1-8

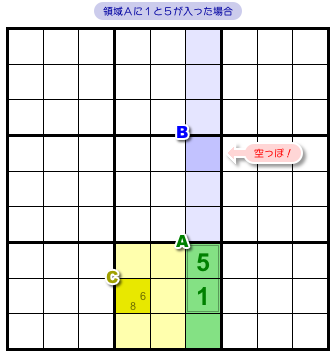
　緑色領域の２マスに数字１と５が同時に入ることはあり得ません。
　マスＢに入る数字がなくなるからです（図1-8）。
　同様に、緑色領域に数字６と８が同時に入ることもありません。
　マスＣに入る数字がなくなっちゃいます。

　領域Ａには候補数字が全４種類ある。マスより２個多い。
　だから、その中の２種類は領域Ａには入れられない。
　そう考えると、次の a. b. が領域Ａの２マスにそれぞれ入ります。

  1. 数字１と５のどちらか。
  2. 数字６と８のどちらか。
図 1-9

　「a. 数字１と５のどちらか」。
　数字１か５のうち一方を領域Ａに入れると、マスＢには他方の数字が入ります。
　よって、青色ヨコ列において数字１と５の入る場所はＡとＢに限定され、他のマスには１も５も入れられません（図1-9 青色＆緑色×印）。

　「b. 数字６と８のどちらか」。
　これも同様です。
　黄色ブロックにおいて数字６と８の入る場所はＡとＣに限定され、他のマスには６も８も入れられません（図1-9 黄色＆緑色×印）。

　図1-7 の結論通りですね😊

２．実際に使ってみよう！

　次は、実際の盤面で Sue De Coq を使ってみましょう。

図 2-1

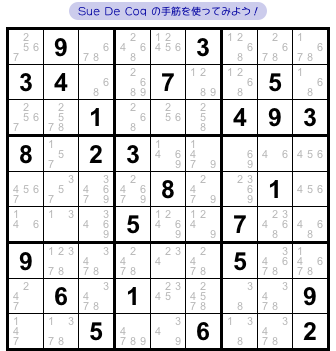
　図2-1 では、とあるマスに数字が判明します。
　それを Sue De Coq で突き止めてみます。

　Sue De Coq を使うためには、とある列とブロックを１個ずつ見つけ、その交差領域と他の２マスに注目しなければいけません。
　さて、それらはどこにあるでしょう？

図 2-2

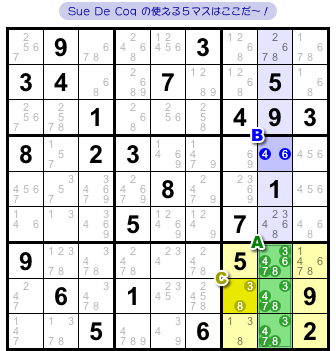
　ここにありました！
　青色タテ列と黄色ブロックが交差した緑色領域、そして、うまいこと青色マスと黄色マスが１個ずつありますね！
　緑色領域をＡ、青色マスをＢ、黄色マスをＣとしておきましょう。

　図2-2 はこういう状況になっています。

  • ５マスが持つ候補数字は３, ４, ６, ７, ８の全５種類。
  • 領域Ａには５種類の候補数字がすべて存在する。
  • マスＢの候補数字は４と６。マスＣの候補数字は３と８。どちらも上記の全５種類のうちの２種類である。
  • ２マスＢ, Ｃに共通する候補数字はない。

　この状況、Sue De Coq が使えますね！
　早速使いましょう！

図 2-3

　前セクションで説明した結論を適用すると、こうなります。

  1. 青色タテ列において、ＡとＢ以外のすべてのマスから候補数字４と６を除去できる。
  2. 黄色ブロックにおいて、ＡとＣ以外のすべてのマスから候補数字３と８を除去できる。
  3. 青色タテ列と黄色ブロックにおいて、Ａ〜Ｃ以外のすべてのマスから候補数字７を除去できる。

　a. は青色×印、b. は黄色×印、c. は黒色×印で示しています。

　理由を簡単に説明します。
　次の a. b. c. が領域Ａの３マスにそれぞれ入ることになるんですね。

  1. 数字４と６のどちらか。
  2. 数字３と８のどちらか。
  3. 数字７。

　んで、数字４と６はＡとＢの２カ所に必ず収まることになり、青色タテ列では候補数字の除去が起こります（青色×印）。
　数字３と８はＡとＣの２カ所に必ず収まることになり、黄色ブロックでは候補数字の除去が起こります（黄色×印）。
　また、黒色×印は「c. 数字７」のおかげです。

図 2-4

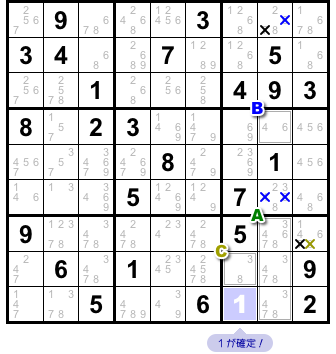
　たくさんの候補数字を除去したところで、Sue De Coq の出番はここで終わり。
　もぅちょっと解き進めてみましょう。

　図2-3 で候補数字を除去したおかげで、候補数字が１個しかないマスが現れちゃいました！
　マスＣのすぐ下ですね。
　そこに数字１が確定するのです。

３．何で「Sue De Coq」という名前なの？

　ここからは余談です。
　このページでは Sue De Coq という解法を紹介してきました。
　もしかしたら、ご覧になった方々は疑問が１つ生じているかもしれません。

「Sue De Coq」なんていう名前、どっから来たの？

　Sue De Coq。
　どう見ても英語には見えない、他の解法とは違って明らかに異質なスペル。
　「de」があるからフランス語とか？　ニワトリの Sue？　Sue って何だ？　ペットのスーちゃん？
　何でこんな名前が付いたんだろうか。

　ナンプレには、古くからとあるフォーラムサイトが存在します。
　『The New Sudoku Players' Forum』というフォーラムサイト。
　そのサイトはナンプレに関するフォーラムで、さまざまな話題で盛り上がっている場所です。
　解法の議論、自作ナンプレの発表、ナンプレの書籍やソフト、その他諸々のトピックがずらっと並び、話題が尽きません。
　Sue De Coq という解法はそのサイトで産声を上げました。

図 3-1

　時は 2005年10月25日、深夜12時を回ったところ。
　ナンプレの解法を発見したというトピックが１つ舞い込んできた。

　その解法の名は『Two-Sector Disjoint Subsets』。
　トピックの投稿者は「ほとんど実用的ではないけど」と前置きしながらも「すごくエレガントな解法だから」とその解法を紹介した。
　ブロックとタテ列の２つを融合させた解法である。

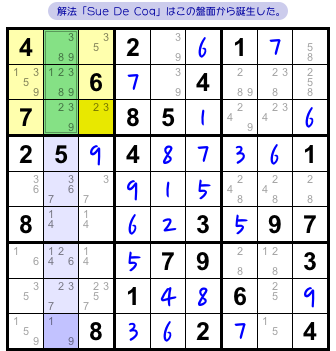
　紹介に使われた盤面は 図3-1 の通り。
　ここから、薄青色＆薄黄色マスから候補数字を４個除去できる。

　理屈は複雑だが、候補数字を大量除去できる画期的な解法であった。
　投稿者も「Magic！」と驚くほどのスグレモノだ。
　しかも、この盤面には同じ手法の使える場所が他に２つも潜んでいる。
　投稿者の言を借りれば、「Sudoku carnage！」がこの盤面には起こるのだ。

　いやはや、ナンプレにはまだまだ面白い解法が眠っているもんだ。
　こんな解法、いったい誰が発見したのだろう？
　そう思い、投稿者欄に目を向けてみる。
　すると、そこにあったのは……「Sue De Coq」という８文字だったのである。

　Sue De Coq 氏は Two-Sector Disjoint Subsets と呼ばれる解法を披露し、「この中に Two-Sector Disjoint Subsets の手筋があるから見つけてね！」とナンプレ２問を置き土産にひとまずトピックを後にする。
　そして、氏の投稿からほどなくして、こういうレスが返ってきた。

Brilliant.
A 'Sue De Coq'😄.

　和訳はちょっと自信ないけれど、「素晴らしい。『Sue De Coq』という名の解法だね😄」といった感じの褒め言葉だろうか。
　続けて、その人は置き土産に対しても解答を返してきた。

I found the 'Sue de Coq' which unlocked your first example:
(図)
In the second example I can see the 'Sue de Coq' but it doesn't seem to provide any eliminations:
(図)

　１つめは無事に Sue De Coq を見つけた模様。
　２つめは Sue De Coq を見つけたものの、先へは進めなかったようだ。
　まぁとにかく、まるで『Sue De Coq』が正式な名前だと言わんばかりだ。

　そのせいかどうかは知らないが、まるで雨後の筍のように他の投稿者達も「Sue De Coq」という名称を使い出す。
　トピックの中に躍る「Sue De Coq」の文字。
　いつの間にやら「Sue De Coq」が解法の名前として浸透してしまっていた。

　……とまぁ、こんな顛末です。
　今では「Sue De Coq」という解法名はフォーラムサイトを飛び出し、全世界のパズラーに知れ渡っています。
　本人が付けた Two-Sector なんちゃらなんて長い名前、今はもぅどこへやら。

　Sue De Coq 誕生の経緯は『The New Sudoku Players' Forum』の Two-Sector Disjoint Subsets というトピックで見られます。
　もし興味があればご覧ください（モバイルでは見づらいかもしれません）。
　……ただ、すべて英語だもんで読むのは大変です😓
　しかも、Sue De Coq 氏本人は数学っぽく抽象論を展開し、トピックの中では解法 Sue De Coq の一般化・抽象化へと話に花が咲いたりしています。
　んもぅマニアックすぎて悶絶すること請け合い😅

参考・参照

更新履歴