1.どういう解法?
W-Wing の舞台は1列。そして、その外側に2マスがいる。
全部で4マスが繰り広げる世界です。
外の2マスは完全な双子で、それが功を奏する解法です。
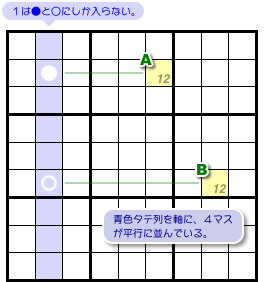
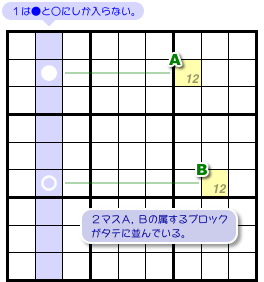
図1-1、青色列を軸とする4マスがありますね。
4マスA, B, ●, ○について、次の状況だとしましょう。
- 青色タテ列において、数字1の入り得るマスは●と○の2つしかない。
- 2マスA, Bに入り得る数字はどちらも1, 2のみ。
- マスAと●は同じヨコ列に属し、マスBと○は同じヨコ列に属している。
図1-1 のような感じですね😄
コの字型っぽい形です。
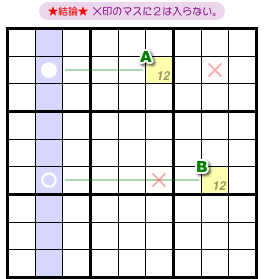
さて、図1-1 からはどういう結論が得られるんでしょう?
こうなるんです。
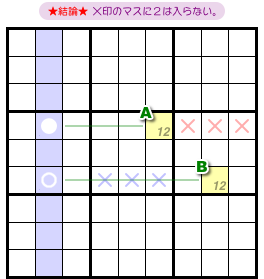
- 2マスA, Bの両方と列を共有するマスが2つある。そのマスに数字2は入らない。
図1-2 だと、×印の2マスが該当します。
上側の×マスはAとヨコ列を共有し、Bとタテ列を共有しています。
下側の×マスはAとタテ列を共有し、Bとヨコ列を共有しています。
このマスに数字2は入らないというわけです。
なぜ、こういう結論になるんでしょう?
それは、2マスA, Bのどちらかに必ず数字2が入るからなんです。
それを解説しましょう。
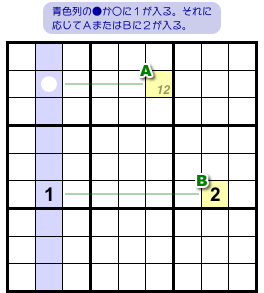
青色タテ列では●と○のどちらかに必ず数字1が入ります。
それぞれ数字1が入った場合はどうなるのか。
見ていきましょう。
●に1が入った場合は、マスAに1は入らなくなります。
つまり、マスAに2が入ることになりますね。
○に1が入った場合は、マスBに1は入らなくなります。
つまり、マスBに2が入ります。
(図1-3 は後者の場合を表しています)
というわけで、次のことが成り立つんです。
- 2マスA, Bの少なくとも一方に必ず数字2が入る。
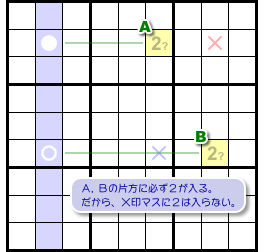
そうなると、数字2を入れられないマスが生じます。
図1-4、×印の2マスです。
赤色×マスはAと同じヨコ列に属し、かつ、Bと同じタテ列にも属しています。
そのため、AとBのどちらに2が入ったとしても赤色×マスに2を入れることができません。
青色×マスはAと同じタテ列に属し、かつ、Bと同じヨコ列にも属しています。
そのため、同様に青色×マスにも2を入れることができません。
図1-2 の結論通りになりましたね😊
これが W-Wing という解法なんです。
上記の例は、タテ1列を軸とした W-Wing でした。
もちろん、ヨコ1列でも理屈は同じです。
それは次セクションで解説していきましょう。
2.実際に使ってみよう!
次は、実際の盤面で W-Wing を使ってみましょう。
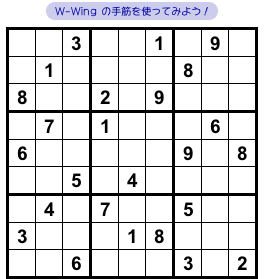
図2-1 では、とあるマスに数字が判明します。
それを W-Wing で突き止めてみます。
ここでは数字4と7に注目します。
数字4を軸として、1列と2マスを探してみます。
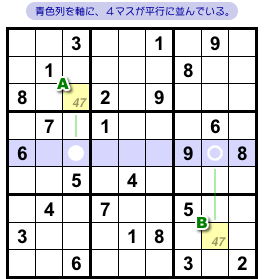
まず、青色のヨコ列に注目します。
この列では、数字4は●と○にしか入りません。
そして、2マスA, Bに入り得る数字はどちらも4, 7のみですね。
しかも、Aは●と同じタテ列に属し、Bは○と同じタテ列に属しています。
さぁ、●, ○, A, Bの4マスが出揃いました!
W-Wing の出番です!
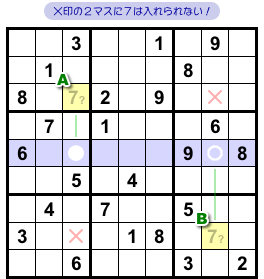
前セクションでの結論を適用すると、こうなります。
- 図2-3、×印のマスに数字7は入らない。
●か○のどちらかに必ず数字4が入ります。
もし●=4なら、A=7になる。
もし○=4なら、B=7になる。
というわけで、A, Bのどちらかに必ず7が入るんです。
となると、数字7を入れられないマスが生じます。
×印の2マスです。
どちらもA, Bとタテ列やヨコ列を共有しています。
AかBに必ず7が入るのだから、×印の2マスに7は入れられないんですね。
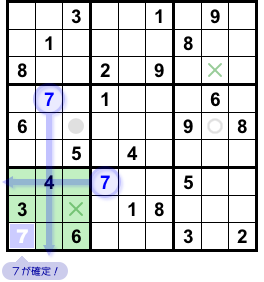
うまく W-Wing が使えましたね!
もぅちょっと解き進めてみましょう。
×印のマスに7が入らないことを踏まえて緑色ブロック(図2-4)に注目します。
なんと、7が判明してしまいました😊
3.他のパターンもあるよ!
これまでのセクションでは、結論は2マスにしか作用しませんでした。
チェーン両端の位置関係によっては、複数のマスに作用することもあるんです。
その例を2つ紹介します。
3-1.パターン・その1
セクション1では、2マスA, Bの属するブロックはタテヨコに並んでいませんでした。
その場合は、結論が2マスにのみ作用しました。
では、A, Bの属するブロックがタテヨコに並んでいる場合はどうでしょう?
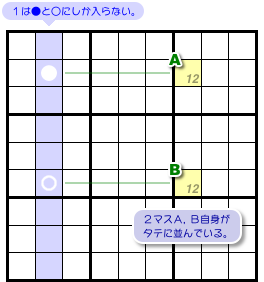
例えば、図3-1 のような場合です。
マスAの所属ブロックとマスBの所属ブロックはタテに並んでいます。
- 青色のタテ列において、数字1の入り得るマスは●と○の2つしかない。
- 2マスA, Bには候補数字が1, 2の2個しかない。
- マスAは●とヨコ列を共有し、マスBは○とヨコ列を共有している。
- 2マスA, B自身はタテに並んでいないが、両者の所属ブロックはタテに並んでいる。

この場合、結論はこうなります。
- 2マスA, Bと列やブロックを共有しているマスがある。そのマスに数字2は入らない。
図3-2 だと、×印の6マスが該当します。
赤色×印マスはマスAとブロックを共有し、マスBとタテ列を共有しています。
青色×印マスはマスAとタテ列を共有し、マスBとブロックを共有しています。
この6マスに数字2は入れられません。
理由は前セクションの説明と同じです。
2マスA, Bのどちらかに必ず数字2が入るからです。
こういうふうに、A, Bの位置関係によっては多くのマスに作用することもあるんですね。
所属ブロックがヨコに並んでいる場合も説明しましょう。
図3-3 の状況だとして、結論はこうなります。
- 2マスA, Bと列やブロックを共有しているマスがある。そのマスに数字2は入らない。
この場合も理由は同じです。
2マスA, Bのどちらかに必ず数字2が入るからですね。
こういうふうに、A, Bの位置関係によっていろんな作用が起こるんですね。
3-2.パターン・その2
例をもうひとつ紹介しましょう。
今度は、別の解法に変わっちゃうパターンです。
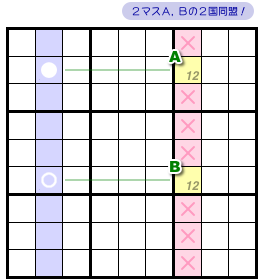
2マスA, Bの持つ候補数字は1, 2の2個だけでした。
そして、その2マスは同じタテ列に属しています。
なんと、2マスA, Bで2国同盟(Naked)が発生しました!
ということは、A, Bの属するタテ列では数字1の入らないマスが大量発生しますね。×印の7マスです。
となると、2マスにしか数字1の入らないタテ列がもう1つ現れました。
そして、よく見ると4マス●, ○, A, Bが矩形状に並んでいるような……。
状況を整理しましょう。
こういう状況になりました。
- 青色&ピンク色の2列において数字1の入り得るマスを探したら、それぞれ2カ所ずつしかなかった。
- 青色の列では●と○のみ。ピンク色の列では△と▲のみ。
- 4マス●○▲△が矩形状に並んでいる。
なんと、X-Wing とまったく同じ状況じゃぁないですか!
W-Wing は X-Wing に姿を変えてしまいました。
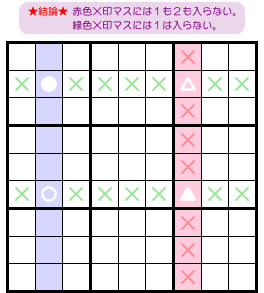
図3-4 で述べたことが起きました😊
最終的な結論を書いておきましょう。
今までの結論とはまるっきり違う😅
- ピンク色タテ列の×印マスには1も2も入らない。
- 緑色×印のマスに1は入らない。
4.そういや『浜田ロジック』って W-Wing に似てるなぁ
W-Wing から派生したわけではありませんが、ナンプレの解法に『浜田ロジック』というものがあります。
このセクションでは、浜田ロジックを W-Wing の視点で語っていこうかと思います。
4-1.浜田ロジックとは?
まずは、浜田ロジックの本来の解法を紹介しましょう。
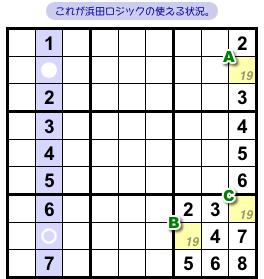
元々、浜田ロジックは 図4-1 の状況で生まれた解法です。
- 青色タテ列において、2マス●, ○に入り得る数字は8と9のみ。
- 3マスA, B, Cに入り得る数字はどれも1と9のみ。
- AとCは同じタテ列に属し、BとCは同じブロックに属している。
- ●とAは同じヨコ列に属し、○とBは同じヨコ列に属している。
この状況からはどういう結論が得られるんでしょう?
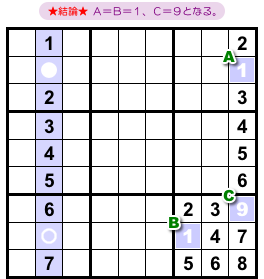
結論はこうなります。
- マスA, Bに数字1が確定し、マスCに数字9が確定する。
なぜ、そうなるんでしょう?
まず、3マスA, B, Cには数字1か9が入りますが、3マスの位置関係からAとBには同じ数字が入ります。
両者に1が入るか、はたまた9が入るか。
対して、青色タテ列では2マス●, ○のどちらかに必ず9が入ります。
となると、AとBの片方には9は入らない。
あらま、A, B両方に数字9を入れるということができなくなっちゃいました。
というわけで、A, B両方には数字1を入れるしかありません。
A=B=1, C=9となるわけですね。
「浜田ロジック」という解法は、パズル作家・浜田剛先生によって発見された解法です。
ちなみに、過去に世界文化社からパズル雑誌『ナンクロ』が刊行されていましたが、浜田先生と筆者(E坂もるむ)はその雑誌にて同時にパズル作家デビューを果たしました。
もぅかれこれ20年以上も前の話です(2022年現在)。
浜田先生はこの「浜田ロジック」の発見などでも活躍がめざましいですが、さてアタシの方は……??
聞かんといて🥺
4-2.浜田ロジックを W-Wing として説明してみる
では、W-Wing の視点で浜田ロジックを見ていきましょう。
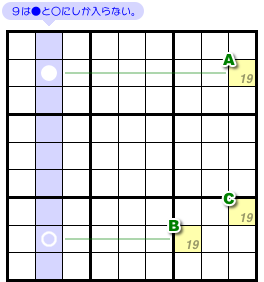
図4-3、青色列を軸とする5マスについて、次の状況だとしましょう。
- 青色のタテ列において、数字9の入り得るマスは●と○の2つのみ。
- 2マスA, Bに入り得る数字はどちらも1, 9のみ。
- マスAと●は同じヨコ列に属し、マスBと○は同じヨコ列に属している。
- マスCは…… あ、W-Wing とは全然関係ないや😅
とととりあえず、数字1と9しか入らないということにしておきます😅
これはセクション3-1で説明した形と同じです。
2マスA, Bの属するブロックがタテに並んでますもんね。
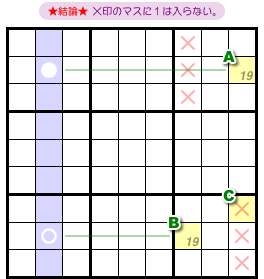
では、セクション3-1で説明した結論を適用してみましょう。
結論はこうなります。
- 2マスA, Bと列やブロックを共有しているマスがある。そのマスに数字1は入らない。
図4-4 だと、×印の6マスが該当します。
この6マスに数字1は入りません。
理由は次の通りです。
2マス●, ○の片方に必ず9が入るから、A, Bの片方に9は入らない。
つまり、A, Bのどちらかには必ず数字1が入るのだから、×印の6マスに数字1は入れられない。
……というわけですね。
あ、よく見たら、マスCに×印がついちゃった!
なんと、マスCに数字1が入らなくなっちゃったんですね。
というわけで、C=9となる。そして、A=B=1となるわけです。
更新履歴
- 2022. 2. 5.
- 新規公開。
- 2023. 3.31.
- ページ冒頭に難易度表記を追加。