【解法】WXYZ-Wing

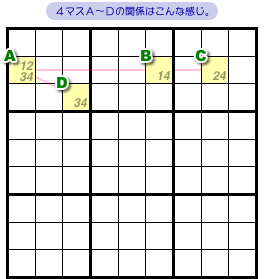
　今、４マスＡ〜Ｄについて、次の状況になっているとします。

• マスＡには数字１〜４のみが入り得る。
• マスＢには数字１と４のみが入り得る。
• マスＣには数字２と４のみが入り得る。
• マスＤには数字３と４のみが入り得る。
• マスＡ, Ｂ, Ｃは同じ列に属している（ただし、ＢもＣもＡとは異なるブロックに属する）。
• マスＡとＤは同じブロックに属している（同じ列に属しても良い）。
• マスＤは３マスＡ〜Ｃとは異なる列に属している。

　んも〜、字だと読む気なくす😅
　図1-1 を見てビジュアル的に理解しちゃってください😅

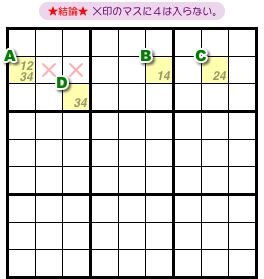
　さて、前図1-1 からはどういう結論が得られるんでしょう？
　こうなります。

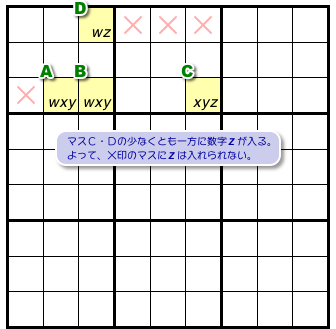
• ４マスＡ〜Ｄすべてと列やブロックを共有するマスがある。そのマスに数字４は入らない。

　図1-2 だと×印の２マスが該当します。
　その２マスはマスＡ〜Ｃとヨコ列を共有し、マスＤとブロックを共有しています。
　その２マスに数字４は入らないというわけです。

　なぜこういう結論になるんでしょう？
　それは、４マスＡ〜Ｄのどこかに必ず数字４が入るからなんです。
　それを解説しましょう。

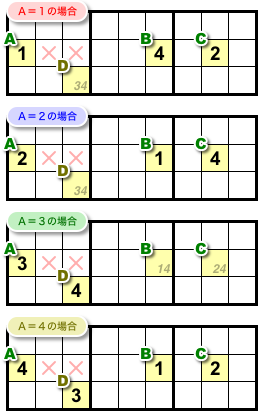
　マスＡの候補は４つあります。
　そして、Ａに入った数字によってマスＢ, Ｃ, Ｄに影響が出ます。

　マスＡに１が入った場合、マスＢに必ず４が入ります（ついでにＣ＝２も確定）。
　マスＡに２が入った場合、マスＣに必ず４が入ります（ついでにＢ＝１も確定）。
　マスＡに３が入った場合、マスＤに必ず４が入ります。
　マスＡに４が入った場合、Ｂ〜Ｄすべて数字が確定します。

　図1-3 の４パターンを見て、どういうことが言えるんでしょう？
　数字４について、何かが見えてきそう……。
　実は、こういうことが言えるんです。

• ４マスＡ〜Ｄのどこかに必ず数字４が入る。

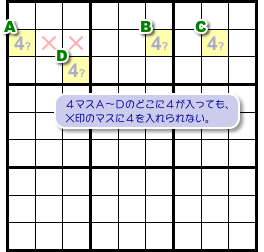
　そうなると、数字４を入れられないマスが生じます。
　図1-4、×印のマスです。

　×マスは３マスＡ〜Ｃとヨコ列を共有し、マスＤとブロックを共有しています。
　だから、Ａ〜Ｄのどこに４が入ったとしても、×マスには４を入れることができないんです。

　図1-2 の結論通りになりましたね😊
　これが従来の WXYZ-Wing です。

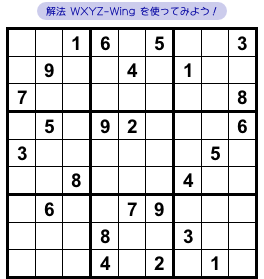
　図2-1 では、とあるマスに数字が判明します。
　それを WXYZ-Wing で突き止めてみます。

　各マスの入り得る数字を調べてみましょう。

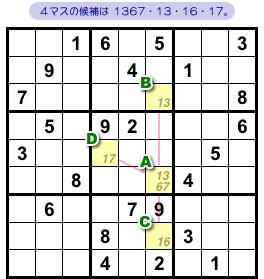
　図2-2、Ａ〜Ｄの４マスに注目します。
　さて、状況はどうなっているでしょう？

• マスＡには数字１, ３, ６, ７のみが入り得る。
• マスＢには数字１と３のみが入り得る。
• マスＣには数字１と６のみが入り得る。
• マスＤには数字１と７のみが入り得る。
• マスＡ, Ｂ, Ｃは同じ列に属している（ただし、ＢもＣもＡとは異なるブロックに属する）。
• マスＡとＤは同じブロックに属している（同じ列に属しても良い）。
• マスＤは３マスＡ〜Ｃとは異なる列に属している。

　これは WXYZ-Wing が使えますね！
　早速使いましょう！

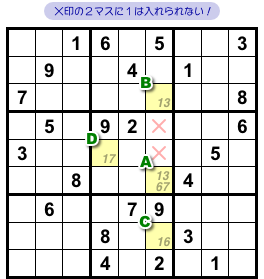
　結論はこうなります。

• 図2-3、×印のマスに数字１は入らない。

　マスＡには１, ３, ６, ７のどれかが必ず入ります。
　すると、入った数字に応じてマスＢ〜Ｄに影響が出ます。

　１が入った場合は、マスＢ〜Ｄすべて数字が確定します。
　３が入った場合は、マスＢに１が入ります。
　６が入った場合は、マスＣに１が入ります。
　７が入った場合は、マスＤに１が入ります。
　結局、４マスＡ〜Ｄのどこかに数字１が入ることになるんですね。

　というわけで、×印のマスに１を入れることができなくなりました（図2-3）。

　うまく WXYZ-Wing が使えましたね！
　もぅちょっと解き進めてみましょう。

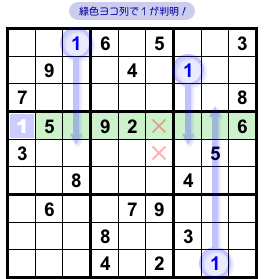
　緑色ヨコ列（図2-4）に注目しましょう。
　×印マスに１が入らないことも踏まえると……

　なんと、緑色ヨコ列で１が判明しちゃいました😊

　まずは、最もシンプルな形。
　これは、図1-1 で挙げたものと同じ形です。
　一応、状況を簡単に説明します。

• マスＡには数字ｗｘｙｚのみが入り得る。
  （中略）
• マスＡ, Ｂ, Ｃは同じ列に属している。
• マスＡとＤは同じブロックに属している。
• マスＤは３マスＡ〜Ｃとは異なる列に属している。

　この場合の結論はこうなります。

• ×印の２マスに数字ｚは入らない。

　理由はセクション１で説明した通りです。
　４マスＡ〜Ｄのどこかに必ず数字ｚが入るからです。

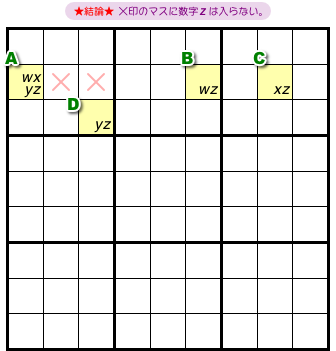
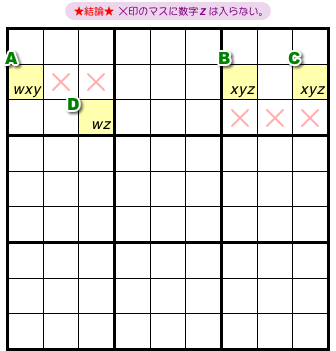
　次は、マスＡから数字ｚがなくなり、他のマスに候補数字がちょびっと増えました。
　この場合の結論はこうなります。

• ×印の５マスに数字ｚは入らない。

　理由は同じです。
　３マスＢ〜Ｄのどこかに必ず数字ｚが入るからです。

　マスＡに数字ｗが入った場合はマスＤに数字ｚが入るため、簡単に上記の結論が得られます。
　マスＡに数字ｘやｙが入った場合は、２マスＢ, Ｃに２国同盟が発生します。そのため、数字ｚはその２マスのどちらかに必ず入り、上記の結論が得られます。

　気が向いた時にでも検証してみてください😊

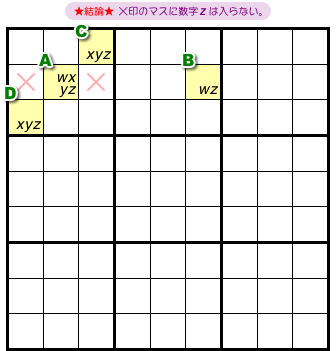
　今度は、ブロックに３マスが入ったパターンです。
　この場合の結論はこうなります。

• ×印の２マスに数字ｚは入らない。

　理由は同じです。
　４マスＡ〜Ｄのどこかに必ず数字ｚが入るからです。

　マスＡに数字ｗが入った場合はマスＢに数字ｚが入るため、簡単に上記の結論が得られます。
　マスＡに数字ｘやｙが入った場合は、２マスＣ, Ｄに２国同盟が発生します。そのため、数字ｚはその２マスのどちらかに必ず入り、上記の結論が得られます。

　気が向いた時にでも検証してみてください😊

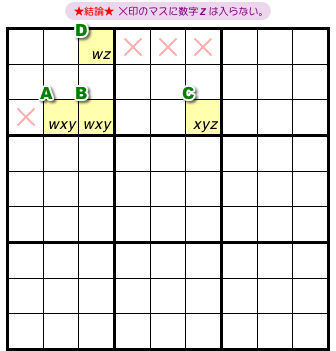
　最後はこんなパターン。
　この場合の結論はこうなります。

• ×印の４マスに数字ｚは入らない。

　理由は同じです。
　２マスＣ, Ｄのどこかに必ず数字ｚが入るからです。

　マスＤに数字ｗが入った場合は、２マスＡ, Ｂに２国同盟（数字ｘ, ｙ）が発生します。そのため、マスＣには数字ｚしか入れられず、上記の結論が得られます。
　マスＤに数字ｚが入った場合は言わずもがな。

　気が向いた時にでも検証してみてください😊

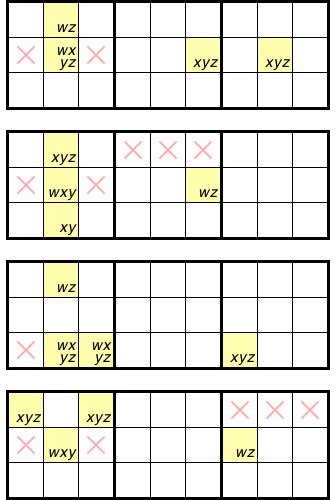
　他にも本当にいろんなパターンがあります。
　んもぅ山ほどありすぎるんで、一部だけ紹介。
　結論も全部同じです。

• ×印のマスに数字ｚは入らない。

　とにかくとにかく、WXYZ-Wing のパターンはこんなにも豊富です。
　んも〜気が遠くなるほど多いんです😅

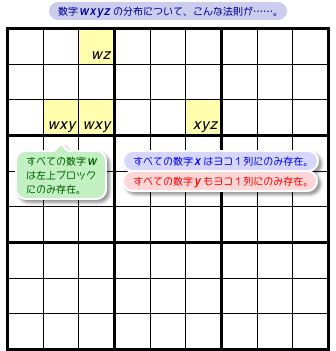
　図4-1、WXYZ-Wing の一例（図3-4 と同じ）です。
　黄色４マスには候補数字がほどよく分布していますね。
　さて、この分布について上記の法則は成り立っているでしょうか？

　実は、成り立っているんです。

• 候補数字ｗはすべて左上ブロックにしか存在していない。
• 候補数字ｘはすべてヨコ１列にしか存在していない。
• 候補数字ｙはすべてヨコ１列にしか存在していない。
• しかし、候補数字ｚだけはそうなっていない。

　ｗ全体、ｘ全体、ｙ全体、どれを見ても１列や１ブロックにスッポリ収まっているんです。
　２つ以上の列やブロックにまたがって存在していないんですね。

　ただし、ｚだけは違います。
　ｚは１列や１ブロックに収まっていません。

　黄色４マスのｗｘｙｚの分布にはこういう大きな法則があるんです。

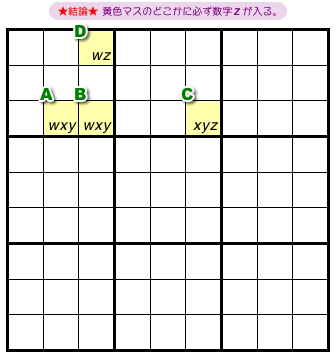
　では、この法則は何をもたらすんでしょう？
　最終的にはこうなるんです。

• 黄色マスのどこかに必ず数字ｚが入る。

　図4-2 だと、マスＣ, Ｄが候補数字ｚを持っています。
　この２マスのどちらかには必ず数字ｚが入る。
　こういうことになるんです。

　なぜ、こうなるんでしょう？
　それを解説しましょう。
　図4-1 で説明した法則が大きく効いてきます。

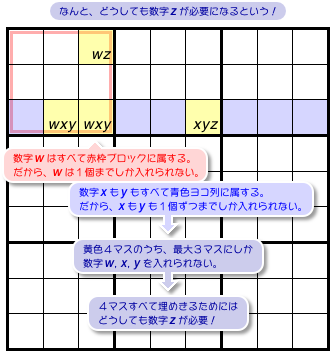
　黄色４マスに数字ｗｘｙｚを入れる場合、実は、必ず成り立つことが１つあるんです。

• 黄色４マスには、ｗもｘもｙも１個までしか入れられない。

　なぜでしょう？
　それは、図4-1 で説明した法則があるから。
　候補数字ｗは１ブロックにしか存在していません。ということは、ｗを１個入れたらもう他の黄色マスにはｗを入れられません。
　候補数字ｘは１列にしか存在していません。ということは、ｘを１個入れたらもう他の黄色マスにはｘを入れられません。
　候補数字ｙも同様です。ｙを１個入れたらそれで終わりです。

　となると、黄色４マスのうち３マスまでなら数字ｗ, ｘ, ｙで埋めることが可能ですね。
　逆に言えば、ｗ, ｘ, ｙだけでは最大３マスまでしか埋まらない。
　あれ？　黄色マスはまだ余ってるよ！
　残りはどうすんの……？

　そうです。残りは数字ｚで埋めるしかないんです。
　ｗ, ｘ, ｙを使い果たしたんだから、もぅｚしかない。
　つまり、４マスすべてを数字で埋めるためには、どうしても数字ｚが必要になっちゃうんですね。

　数字ｗ, ｘ, ｙだけでは黄色４マスを埋め尽くせない。
　どうしても数字ｚが必要になってしまう。
　というわけで、黄色４マスについてこういう結果になるんです。

• 黄色４マスのどこかに必ず数字ｚを入れなければならない。

　ま、「黄色４マスのどこか」とは言っても、実際はマスＣ, Ｄにしか数字ｚを入れる余地はありません。
　そのどちらかには必ず数字ｚが入る、というわけですね。
　どちらに数字ｚが入ろうとも、×印のマスに数字ｚは入らないということがわかるんです。

　図4-2 の結論通りになりましたね😊