【解法】X-Wing

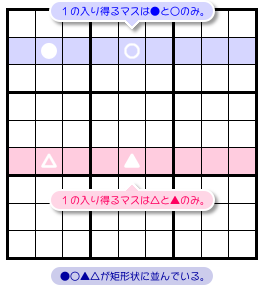
　図1-1 の青色＆ピンク色のヨコ２列を見てみましょう。
　この２列において数字１の入り得るマスを探したら、次の状況だったとします。

• 青色ヨコ列において、数字１は●と○にしか入らない。
• ピンク色ヨコ列において、数字１は△と▲にしか入らない。
• ４マス●○▲△は矩形状に並んでいる。

　実は、矩形状というのが大きなミソでして。
　ヨコ２列に並んだ４マス達が、今度はタテ２列に大きな影響を及ぼしていくんです。

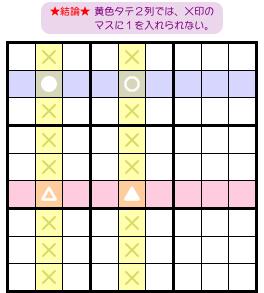
　さて、前図1-1 からはどういう結論が得られるんでしょう？
　こうなるんです。

• ●と△の属するタテ列では、●と△以外のマスに数字１は入らない。
• ○と▲の属するタテ列では、○と▲以外のマスに数字１は入らない。

　図1-2 だと、×印のマスが該当します。
　このマスに数字１を入れられなくなるんです。
　うわ〜なんという凄まじいバツっぷり！　タテ２列がバッサリ！
　こんなにも数字１が入らなくなっちゃうんですね。

　なぜ、こういう結論になるんでしょう？
　それは、次の２つが判明することになるからです。

• ●と△のどちらかに必ず数字１が入る。
• ○と▲のどちらかに必ず数字１が入る。

　それを解説しましょう。

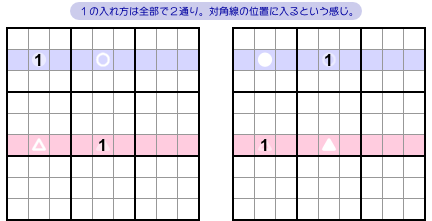
　まず、●○▲△のうち２マスにだけ数字１が入ることはすぐにわかります。ヨコ列に１個ずつですね。
　そして、●○▲△が矩形状に並んでいることから、数字１の入れ方は次の２通りしかありません。

• ●と▲の２マスに入れる。
• ○と△の２マスに入れる。

　対角線の位置に数字１が並ぶわけですね。
　同じ数字をタテにもヨコにも並べるわけにはいかないから、ナナメに並べるしかないんです。

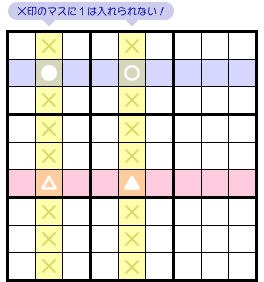
　●と▲に１が入る。
　○と△に１が入る。
　この２通りから何が言えるのか。

　実は、その２通りのどちらであったとしても、次の２つが成り立つんです。

• ●と△のどちらかに必ず数字１が入る。
• ○と▲のどちらかに必ず数字１が入る。

　前者により、左側の黄色タテ列では●と△以外のマスに１は入れられません。
　後者により、右側の黄色タテ列では○と▲以外のマスに１は入れられません。
　というわけで、２列にわたって数字１を入れられなくなっちゃうんです。

　図1-2 の結論通りになりましたね😄
　これが X-Wing という解法です。
　２列まるごと数字１が入らないという！
　ずいぶん豪快な結末になりましたね。

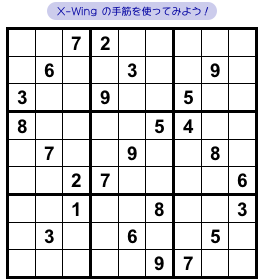
　図2-1 では、とあるマスに数字が判明します。
　それを X-Wing で突き止めてみます。

　ここでは数字９に注目して、９の入り得るマスを探してみます。

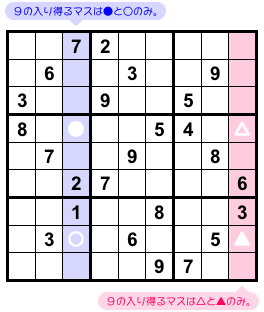
　青色とピンク色の２列に注目しましょう。

　両者を調べると、数字９はともに２カ所にしか入れられません。
　青色の列では●と○の２つ。
　ピンク色の列では△と▲の２つですね（図2-2）。

　そして、●○▲△の４マスは……おぉ！　ちょうど矩形状に並んでる！
　まさに X-Wing の使える形ですね。
　使ってみましょう！

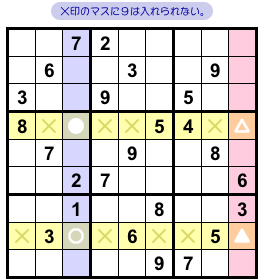
　セクション１で説明した通り、４マス●○▲△については次のどちらかが成り立ちます。

• ●と▲の２マスに数字９が入る。
• ○と△の２マスに数字９が入る。

　そのため、●と△のどちらかに必ず９が入ります。
　だから、上側の黄色ヨコ列では×印のマスに９を入れられません（図2-3）。

　同様に、○と▲のどちらかに必ず９が入ります。
　だから、下側の黄色ヨコ列でも×印のマスに９を入れられません（図2-3）。

　なんと、８マスも数字９が入らなくなっちゃいました！

　うまく X-Wing が使えましたね！
　もぅちょっと解き進めてみましょう。

　★マス（図2-4）に注目しましょう。
　前図2-3 での説明により「★マスに９を入れられなくなっている」ということに注意してください。

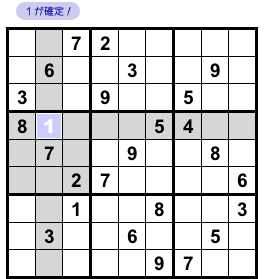
　★マスの属する列やブロック全域に目を通すと、★マスには１と９しか入れられないことがわかります。
　そして、★マスには９が入らないということも既に判明しています。

　というわけで、★マスに１が確定しちゃいました😄