1.Fish が退化する !?
Sashimi Swordish は Finned Swordfish とほとんど同じですが、1つだけ違うところがあります。
それは Fish が退化するというところです。
と言っても、「じゃぁ退化って何だ?」ですよね😓
そこで、このセクションでは Fish の退化について解説していきます。
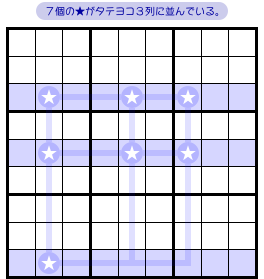
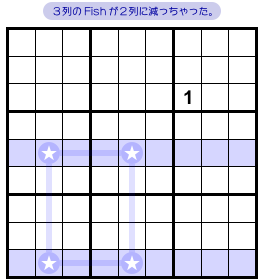
図1-1 を見てみましょう。
青色3列において、数字1の入り得るマスは★の7カ所しかなかったとします。
これらの★マスがヨコ3列に並んでいるというのは当たり前😊
そして、タテ3列にも並んでいますね。
また、整列は少し欠けています。
しかし、Swordfish のページで補足説明した通り、これは正当な整列です。
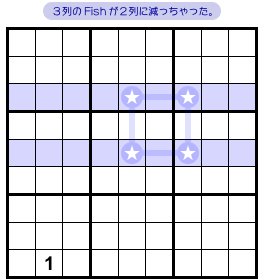
さて。
前図1-1 の盤面、★の配置をよく見ると……とあることに気付きます。
一番下のヨコ列には★が1個しかありません。
あれ? その列に数字1が確定しちゃうじゃぁないか!
じゃぁ、1を入れちゃいましょう。
すると、他の2列は★マスが2個ずつに減ってしまいました。
なんと!
Swordfish が X-Wing に変わっちゃったよ!
★の配置によっては、こういうことが起こるんです。
一部のマスに数字1が確定したりして列数が減ってしまう。
このように、元の Fish から列数が減ってしまい、小サイズの Fish に姿を変えてしまうことを Fish が退化する と言います。
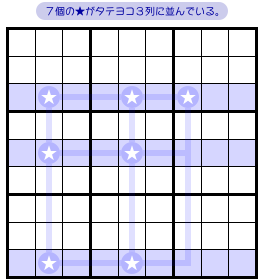
もうひとつ例を紹介しましょう。
今度はどの青色列にも★が2個以上あります。
ただ、あるタテ列には★が1個しかありません。
どの青色列を見ても数字1は確定しません。
この Fish は退化しなさそうに見えますね。
ところが、これも退化するんです。
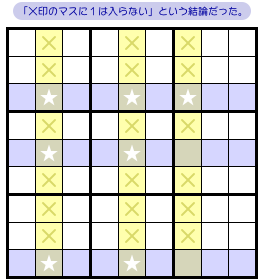
なぜでしょう?
それは、Swordfish にはこういう結論があるからです。
- 黄色タテ列において、★以外のマスに数字1は入らない。
つまり、図1-4 の黄色マスに数字1は入れられない。
★以外の黄色マス、全滅!
……だったわけですね。
というわけで、右側のタテ列では数字1は★マスに入るしかない。
すると、他の青色2列では★マスが2個ずつに減っちゃいます。
Swordfish は X-Wing に退化するんですね。
退化のパターンはいくつかあります。
簡単なのは、上記のように1サイズ縮小するパターンですね。
他には、Jellyfish が2個の X-Wing に分かれたりします。4列のように見えて実は2列×2だったという……。
極端な場合だと、どの列にも次々と数字1が確定してしまって Fish 自体が消滅!……なんてこともあったり。
退化を通り越して絶滅である😅
このページでは、退化について簡単な捉え方で済ませることにします。
「ある1マスに数字が確定して Fish が1サイズ小さくなる」というパターンのみを扱うことにします。
Sashimi 型の Fish 系解法では、この Fish の退化が関わってきます。
それを踏まえながら、以降のセクションをご覧ください。
2.どういう解法?
Sashimi Swordfish の舞台は Finned Swordfish と同じ。平行な3列。
Finned Swordfish との違いはほんの少ししかありません。
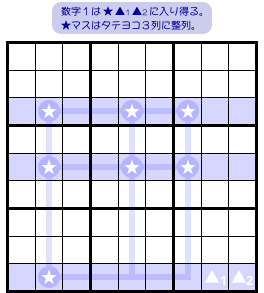
図1-1、青色3列を見てみましょう。
この3列において数字1の入り得るマスを探したら、★ ▲1 ▲2 の9カ所しかなかったとします。
これら9マスには次の特徴があります。
- 7個の★がタテヨコ3列に整列している。
- ある青色1列には★は1個しかないが、▲1 ▲2 が属している。ただし、▲1 ▲2 は★と同じブロックには属していない。
- ★マスの属するタテ列には ▲1 も ▲2 もない。
図2-1 では、一番下のヨコ列に大きな特徴がありますね。
▲1 ▲2 の属するヨコ列には★が1個しかありません。
ここで、用語をひとつ紹介しましょう。
図2-1 では、整列とは無関係そうに ▲1 ▲2 が佇んでいました。これを fin と呼びます。
fin は「ひれ」という意味です。
Sashimi Swordfish にも fin という概念があり、それは Finned Swordfish と同じものを指します。
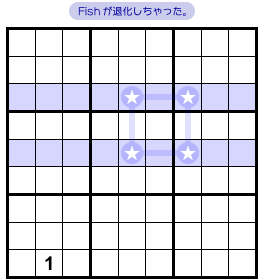
さて、この Fish には大きな特徴があるんです。
- fin をすべて取り除くと Fish が退化する。
仮に ▲1 ▲2 を消してみましょうか。
すると、一番下のヨコ列には★マスが1個だけになりますね!
数字1が確定しちゃう。1を入れちゃいましょう。
すると……
Swordfish が X-Wing に退化した。
こういうふうに、fin がないと Fish が退化する。
これが Sashimi 型の Fish なんです。
さて、この Sashimi Swordfish ですが……実は、本質的には Finned Swordfish とまったく同じです。
なぜなら、Fish の形が本質的に同じだから。
どちらも「★マスのタテヨコ整列に fin が付いている」という形なんですね。
両者の違いはただ1つ。
仮に fin を全消ししたら Fish が退化する? それとも退化しない?
それだけ😅
前者を Sashimi、後者を Finned と区別しているだけなんです。
というわけで、Finned Swordfish をご存じの方々はここから先を読む必要はありません。
だって、結論は同じだし、論理展開も同じなんですもの!
でも、一応、Sashimi Swordfish を解説していきます。
Sashimi の詳細については Sashiminess のページで紹介しています。よければご覧ください。
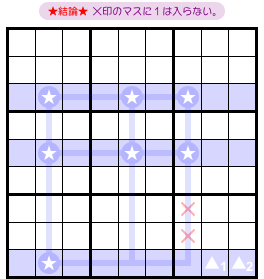
さて、前図2-1 からはどういう結論が得られるんでしょう?
こうなるんです。
- ★マスの属するタテ列、▲1 ▲2 の属するブロック、この両者に共通する2マスがある。そのマスに数字1は入らない。
図2-3 だと×印の2マスが該当します。
この2マスは右側の★マス2つと同じタテ列に属しています。同時に、▲1 ▲2 と同じブロックに属しています。
この2マスに数字1は入らなくなるというわけです。
なぜ、こういう結論になるんでしょう?
それを解説しましょう。

数字1の入り方について、大きく分けて2つの場合があります。
- ▲1 ▲2 のどちらかに数字1が入る。
- ▲1 ▲2 の両方ともに数字1が入らない。
この両者についてそれぞれ検証していきましょう。
まずは前者。
これは簡単です。
▲1 ▲2 のどちらに数字1が入ろうとも、同じブロック全体に数字1が入らなくなります(図2-4 ×印)。

次に後者。
この場合は、fin がすべてなくなります。
つまり、ただの Swordfish に様変わり!
ただ、一番下のヨコ列では数字1は★マスに確定しますね。
すると、Swordfish はさらに X-Wing に退化しちゃいました。
ということで、X-Wing の結論の通り、★以外のすべての黄色マスに数字1が入らなくなります。
★以外の黄色マス、全滅!(図2-5)
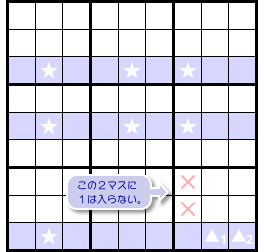
図2-4 と 図2-5、両者のうち一方が成り立ちます。
2つの図を見比べてみると……おぉ、共通して×印のついているマスがありますね!
そのマスに数字1は入らないということが言えるんです。
具体的には 図2-6 の2マスです。
図2-3 の結論通りになりましたね😄
これが Sashimi Swordfish です。
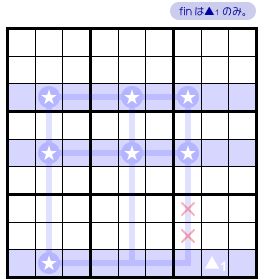
図2-1 では、fin は ▲1 ▲2 と2つありました。
Finned Swordfish と同様、fin は1つしかなくてもかまいません。
この場合でも、まったく同じ論理展開ができます。
そのため、×印のマスに数字1を入れることができません。
ちなみに、fin が1つもない場合はただの Swordfish です。
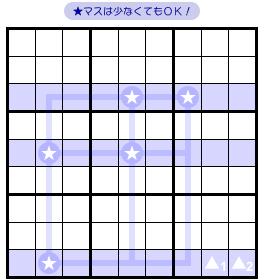
図2-1 では、7個の★がタテヨコ3列に整列していました。
しかし、本当は★がキッチリ7個並んでいる必要はありません。
★が少なくても、まったく同じ論理展開ができます。
大事なのは、★がタテにもヨコにも整列しているということです。
それさえ満たしていれば、★の個数は関係ありません。
ただし、fin を全消しして Fish が退化する形でなければいけません。
でないと Sashimi にはなりません。
上記の例では、青色はヨコ列でした。
もちろん、タテ列の場合でも理屈は同じです(その場合、fin はタテに並びます)。
その場合は、セクション3で実例を挙げて説明していきましょう。
3.実際に使ってみよう!
では、実際に Sashimi Swordfish を使ってみましょう!
前セクションでも述べた通り、解き方に関して Sashimi Swordfish と Finned Swordfish は同じです。
だから、Finned Swordfish をご存じの方々は読む必要はありません。
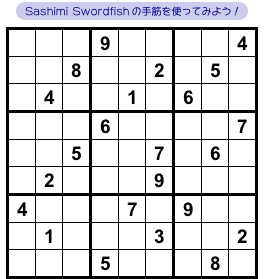
図3-1 では、とあるマスに数字が判明します。
それを Sashimi Swordfish で突き止めてみます。
ここでは数字4に注目して、4の入り得るマスを探してみます。
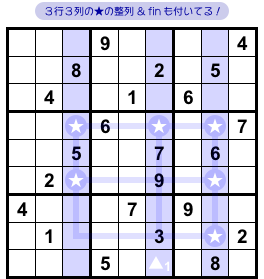
青色の3列に注目しましょう。
この3列では、数字4の入り得るマスは 図3-2 の通りです。
★ ▲1 の合計7個。
6個の★を見ると、タテヨコ3列に整列していますね。
そして、fin ▲1 も付いている。
詳細は省きますが、他にも Sashimi の諸条件を満たしています。
さぁ、これはもぅ Sashimi Swordfish の出番です!
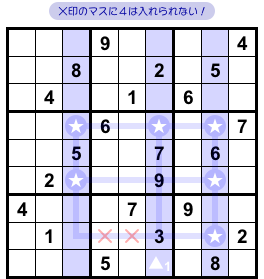
前セクションでも結論を 図3-2 に適用してみましょう。
すると、次のことが成り立ちます。
- ★マスの属するヨコ列、▲1 の属するブロック、この両者に共通するマスがある。そのマスに数字4は入らない。
理由は前セクションと同じです。
次の2通りに場合分けして検証すればOKです。
- ▲1 に数字4が入る場合。
- ▲1 に数字4が入らない場合。
というわけで、×印のマスに数字4を入れることができなくなりました。
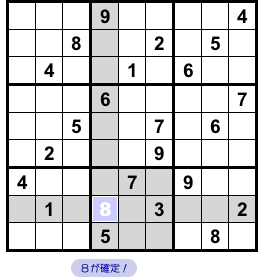
うまく Sashimi Swordfish が使えましたね!
もぅちょっと解き進めてみましょう。
図3-3 の×印マスのうち、左側の方に注目しましょう。
そのマスの属する列やブロック全域に目を通すと、そのマスの候補数字は4と8しかないことがわかります。
そして、×印マスに4が入らないことも既に判明しています。
というわけで、8が確定しちゃいました😄
更新履歴
- 2022. 2. 5.
- 新規公開。
- 2023. 3.31.
- ページ冒頭に難易度表記を追加。