【解法】Unique Rectangle

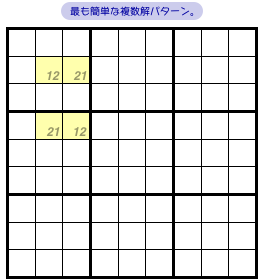
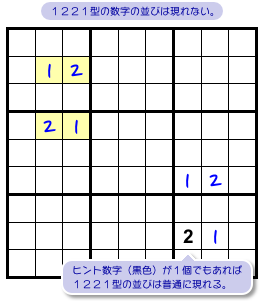
　図1-1 を見てみましょう。
　黄色４マスが矩形状に並んでいますね。
　この４マスは次の状況になっています。

• 黄色４マスは、タテ２列・ヨコ２列・ブロック２個にのみ属している。
• どの黄色マスも候補数字は２つだけ。しかも、すべて同じ。

　黄色マスを含むヨコ列は２つあります（２行目と４行目）。
　黄色マスを含むタテ列は２つあります（２列目と３列目）。
　黄色マスを含むブロックは２つあります（左上とそのすぐ下）。
　そして、どの黄色マスも数字１と２しか入れられません。

　こういう特徴があるんですね。

　ナンプレを解く上で 前図1-1 のような箇所があると、不都合が生じます。
　最後まで解き終えることができないんです。

　一応、うまいこと解き進められれば、図1-2 のように 77マスまでなら数字で埋められるかもしれません。
　ところが、これ以上マスが埋まらない。
　どうしてもここから先へ進めない！

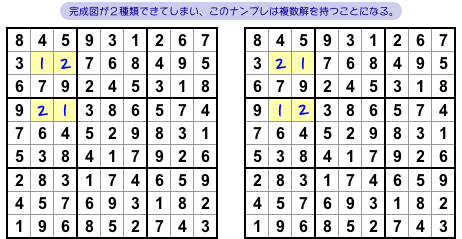
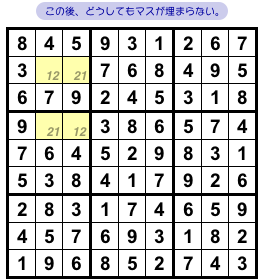
　それもそのはずで、前図1-2 の状況からは完成図を２種類作ることができるんです。
　図1-3 ですね。

　黄色マスのどれか１つに数字１を入れても数字２を入れても完成できてしまう。
　もちろん、両者の完成図は異なるから、解が複数あるわけなんです。

　結局、図1-1 の状況が生まれてしまった時点で、そのナンプレは必ず複数解を持つ。
　これはどうしても免れないんです。

　前図1-3 に関連して、もうひとつ注意すべきことがあります。

• 解いている途中で 図1-4 左上のような数字の並びは絶対に現れない。

　この黄色４マスの数字はヒント数字（問題図に最初からある数字）ではなく、解いている途中で書き込まれた数字です。
　何もないところから１２２１の形は生まれないということですね。

　なぜかというと、たとえこの状態から 前図1-3 左側のように完成したとしても、この４マスの１と２を交換して 図1-3 右側の形にもできてしまうからです。
　１２２１の形が生じた時点で、もう複数解は免れないんですね。
　だから、この１２２１型の並びは現れません。

　ただし、図1-4 右下のように４つのうちどれか１つでもヒント数字（黒色）だったなら、１２２１型は普通に現れます。

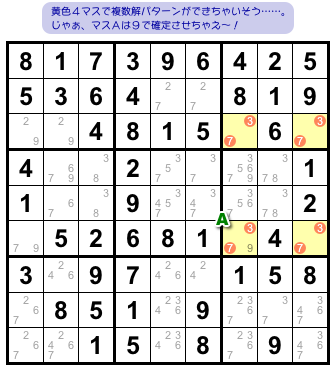
　まずは簡単な例を。
　図2-1、矩形状に並んだ黄色４マスを見てみましょう。
　この４マスには候補数字３と７がありますね。
　そして、マスＡにだけ候補数字９もオマケで付いています。

　この候補数字９のように、複数解パターンに直接関わらない候補数字のことをここでは オマケ候補 と呼ぶことにしましょう。

　この場合、こういう結論になります。

• マスＡに数字９が確定する。

　なぜでしょう？
　それは、もしマスＡに数字９が入らないと仮定すると、図1-1 で紹介した複数解パターンが現れてしまうからです。
　それは避けなければいけないから、マスＡには９を入れなければいけないんです。

　図2-1 の場合はマスＡのオマケ候補が９しかないので、すぐにマスＡに９が確定しました。
　一般には「候補数字３と７が複数解パターンを作っちゃうから、オマケ候補のどれかがマスＡに入る」と解釈すると良いでしょう。

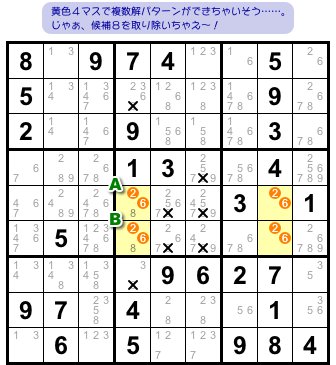
　２つめはこんな感じ。
　図2-1 と同様に、黄色４マスが矩形状に並んでいます。
　共通の候補数字は２と６。
　そして、２マスＡ, Ｂには候補数字８もオマケで付いています。

　この場合、こういう結論になります。

• ２マスＡ, Ｂと列やブロックを共有しているマスから候補数字８を除去できる。

　図2-2 だと、×印の箇所です。
　これらの候補数字８が除去されるんです。
　なぜかと言うと、もしマスＡ, Ｂ両方とも候補８を除去してしまうと、複数解パターンが現れてしまうからです。
　それは避けなければいけないから、マスＡ, Ｂのどちらかに必ず８が入ると考えなければいけない。

　よって、Ａ, Ｂの属するタテ列やブロックから候補数字８が大量除去されることになるんです。

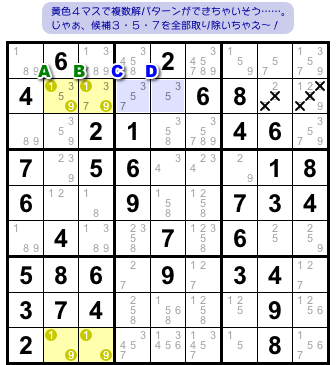
　例をもうひとつ！
　今度はだいぶ複雑です。
　同様に黄色４マスが矩形状。共通の候補数字は１と９です。
　２マスＡ, Ｂのオマケ候補は３, ５, ７。
　この場合の結論はこうなります。

• オマケ候補３, ５, ７を全部除去できるマスが生じる。

　図2-3 のミソは２マスＣ, Ｄの候補数字も３, ５, ７だということ。
　Ａ, Ｂのオマケ候補とまったく同じなんです。

　複数解パターンを避けるためには、「マスＡに３か５が入る」「マスＢに３か７が入る」のどちらかが必要です。
　前者の場合、２マスＡ, Ｄで数字３と５の２国同盟ができ、そのおかげでマスＣに７が確定します。Ａ, Ｃ, Ｄの３マスを３, ５, ７が占拠することになります。
　後者の場合、３マスＢ, Ｃ, Ｄで３国同盟ができ、その３マスを３, ５, ７が占拠することになります。
　どちらにしても、上から２つめのヨコ列において３マスに数字３, ５, ７が占拠してしまう形ができあがります。

　よって、右端の２マスには３も５も７も入れられなくなるんです。

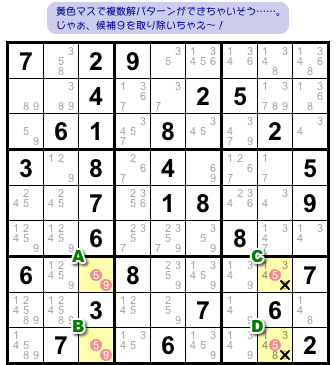
　これでラスト！
　ていうか、例ばっかりでホントすいません😅

　同様に黄色４マスが矩形状。
　共通の候補数字は５と９です。
　今回の結論はこうなります。

• ２マスＣ, Ｄから候補数字９を除去できる。

　今回はオマケ候補は重要ではなく、候補数字５が重要です。
　２マスＣ, Ｄを含むタテ列（またはブロック）を見ると、５の入り得るマスはＣ, Ｄしかありません。

　そうなると、ＣとＤのどちらかに必ず５が入ります。
　それに応じて、ＡとＢに５と９が１個ずつ確定します。
　結果、Ａ〜Ｄのうち３マスに５, ９, ５が入ることが約束されました。
　ということは、もし最後の１マスに９が入ったとしたら……複数解パターンができてしまうんです。

　だから、ＣにもＤにも９を入れてはいけないんです。

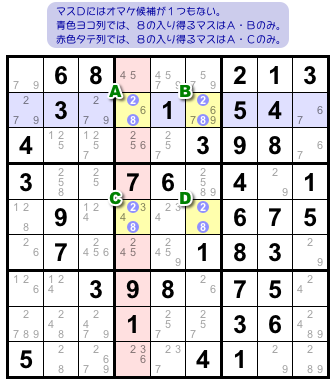
　図3-1、矩形状に並んだ黄色４マスＡ〜Ｄを見てみましょう。
　この４マスには共通の候補数字２と８がありますね。
　そして、オマケ候補のないマスが最低１つあります。それ以外の３マスのうち２マス以上がオマケ候補を持っています。

　この状況の場合、注目すべきマスが２つあります。
　オマケ候補を持たないマスと、その対角に位置するマスです。
　図3-1 だと、マスＤとＡの２つです。

　この２マスには特徴があります。
　まず、マスＤにはオマケ候補が１つもありません。
　そして、マスＡの属するタテヨコ２列を見てみると、ヨコ列では８の入り得るマスはＡとＢの２つしかなく、タテ列では８の入り得るマスはＡとＣの２つしかありません。

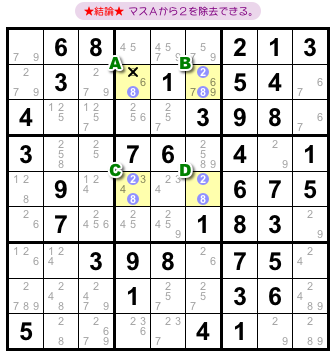
　さて、この状況からどういう結論が得られるんでしょう？
　こうなるんです。

• マスＡから候補数字２を除去できる。

　なぜ、こういう結論になるんでしょう？
　それは、マスＡに数字２を入れると複数解パターンができてしまうからなんです。
　もちろん、それは避けなければいけない。
　マスＡから候補数字２をはずさないといけなくなるんです。

　それを解説しましょう。

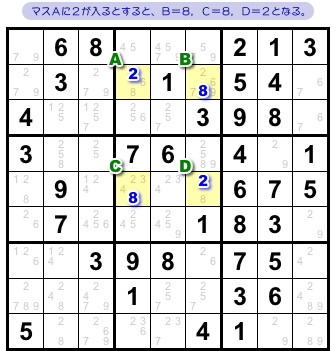
　今、マスＡに数字２が入ったと仮定しましょう。
　すると、Ａの属するヨコ列ではマスＢにしか８は入らなくなります。
　Ａの属するタテ列ではマスＣにしか８は入らなくなります。
　そのため、マスＤには自動的に２が入ることになります。
　その結果、Ａ〜Ｄの４マスに２８８２がそれぞれ確定しますね。
　図3-3 の通りになりました。

　……あれ？
　この４マス、複数解パターンじゃん！！

　そうなんです。
　２８８２の形の並びになってしまって、複数解パターンができあがってしまう！
　これは避けなければいけません。
　だから、マスＡに数字２を入れてはいけないわけなんです。

　図3-2 の結論通りになりましたね😊

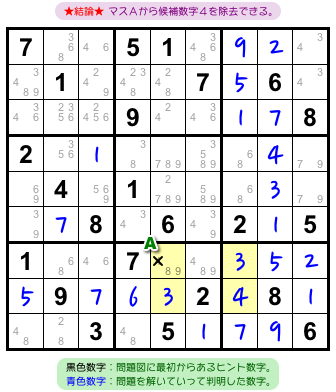
　図4-1 は、解いている途中のナンプレ盤面です。
　問題図に最初からあるヒント数字は黒色、解いている途中で判明した数字は青色で示しています。

　ここで、黄色４マスに注目してみましょう。
　４マスのうち３マスが３, ３, ４で埋まっていますね。
　この場合、こういう結論になるんです。

• マスＡに数字４は入らない。

　なぜか？
　それは、マスＡに数字４が入ると複数解パターンができあがってしまうからです。
　それは避けなければいけないから、マスＡから候補数字４を除去しないといけなくなるわけですね。

　すでに埋まっている３, ３, ４はすべて問題図にはなかった数字。
　これがこの解法のミソでして。
　もし黄色４マスのどこかにヒント数字があったなら、話はまったく違います。４３３４の形は普通に現れます。
　これは 図1-4 でも説明しています。