1.「数字xのn列ネット」になる例

ピンク色の3列において1の入り得るマスを探したとき、図1のように3ヵ所ずつあったとします(他のピンク色マスに1は入りません。以下同様)。
これらの1はタテ方向に3列並んでいます。
そして、ヨコ方向にも3列並んでいます。
タテ方向・ヨコ方向ともに同じ列数 ですね。
これは『数字1の3列ネット』です。
最もわかりやすいタイプのネットワークです。
- n本のタテ列において数字xの入り得るマスを調べたとき、それらのマスがヨコ方向にもn列並んでいたとする。
このとき、その状態を 数字xのn列ネット と呼ぶ。
(上記において、タテとヨコを入れかえても可)
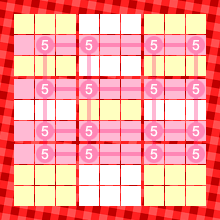
ピンク色の4列に対して5の入り得るマスを調べたら、図2のようになったとします。
タテにも4列並びました。タテヨコともに同じ列数です。
『数字5の4列ネット』ですね。

数字はキッチリn×n個でなくてもかまいません。
ところどころ抜けていてもかまいません。
図3のように、一部の列には4が2個しかないですが、タテヨコ3列ずつ並んでいますね。
立派な『数字4の3列ネット』です。

どの列を見ても7は2〜3個しか入ってなくてネットのように見えません。
でも、タテヨコともに5列ずつ並んでいるのがわかります。
これも立派な『数字7の5列ネット』です。
2.「数字xのn列ネット」にならない例
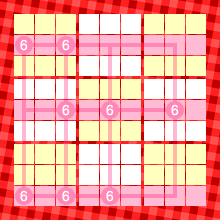
ピンク色の3列において6の入り得るマスを探したとき、図5のようになったとします(他のピンク色マスに6は入りません)。
これらの6は ヨコ方向に3列並んでいます。
しかし、タテ方向には4列並んでいます。
『数字xのn列ネット』になるためには、タテ・ヨコともに同じ列数でなければいけません。
なので、これは数字6のネットとは言いません。
- n本のタテ列において数字xの入り得るマスを調べたとき、それらのマスがヨコ方向にもn列並んでいたとする。
このとき、その状態を 数字xのn列ネット と呼ぶ。
(上記において、タテとヨコを入れかえても可)

一般には、『数字xのn列ネット』はなかなか見つかりません。
図6において数字3の入り得るマスを★で示しましたが、どう頑張ってもネットはひとつも見つからない。
数字xの入り得るマスを全部探すこと自体、大変な作業です。
なので、数字xのn列ネットを見つけるのはさらに大変。
しかし、一度見つけてしまうと数字を入れられるマスが一挙に限定されるので、先に進める可能性が出てきます。