1.「対角線のどちらか」法

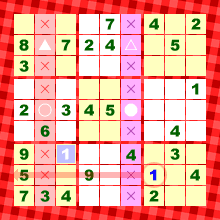
図1を見てみましょう。
結論を言ってしまうと、実は★マスに1が入るんです。
なぜでしょう?
今は★マスから離れて、オレンジ色の2列に注目しましょう。

オレンジ色の2列において1の入り得るマスを探してみます。
上の列では、1は▲と△のどちらかに入りますね。
下の列では、1は○と●のどちらかに入ります。
さらに、よく見ると、▲△●○の4つは長方形状に並んでいます。
実はここがミソ!
上記の解説により、▲△●○のうち2マスに1が入ることはわかりますね。
そして、同じタテ列に同じ数字は入れられないのだから、2つの1の入れ方として「▲と●に入る」「△と○に入る」の2通りしかないことがわかります。
まるで対角線のどちらか一方に1が入るという感じですね。
すると、どういうことが言えるのか。
実は、その2通りのどちらであったとしても ▲と○のどちらか片方に必ず1が入る ということが言えてしまうんです。
ということは、赤色の列において1の入り得るマスは▲と○の2ヵ所に限定され、×印のマスには1を入れられないことがわかる。
これと、右下ブロックの1からのレーザーを考えると……。
左下ブロックでは1が確定してしまうんです。
さらに言うと、上記と同時に △と●のどちらか片方に必ず1が入る ということも言えます。
よって、同様に考えれば、紫色の列では×マスに1を入れられないことになります。
2.「数字のネットワークをさがせ」法

まず、解き方を解説する前に、ひとつ定義をします。
今、ピンク色の3列において7の入り得るマスを探したとき、図4のように3ヵ所ずつあったとしましょう(他のピンク色マスに7は入りません)。
これらの7を見てみると「タテ方向に3列並んでいる」のは当然ですが、なんと ヨコ方向にも3列並んでいます。
そして、タテとヨコの列数がまったく同じ!
- n本のタテ列において数字xの入り得るマスを探したとき、それらのマスがヨコ方向にもn列並んでいたとする。
このとき、その状態を 数字xのn列ネット と呼ぶことする。
(上記の定義において、タテとヨコを入れかえても可)
なんともダサいネーミングでホントすいません😅
図4の場合は『数字7の3列ネット』となりますね。
このページで例をいくつか挙げてみました(別ウインドウで開きます)。

図4では『数字xのn列ネット』を定義しました。
果たして、このネットには何の意味があるのか?
図4のピンク色3列において、7の入れられるマスを★としましょう。
★マスのどこに7が入るかは まったく確定できません。しかし、7の入れ方のパターンはいろいろありますね。6通りあります。
時間があれば、その6通りの各パターンをすべて試してみてください。
★以外のピンク色マスに7が入らないことに注意し、もちろん同じ列に7を複数入れないようにしながら。
さぁ、どうでしょう。
オレンジ色の3列において★は各3つずつありますが、どの列を見ても3つの★のどこかに必ず7が入ってしまう はずです。
ということは、7の入れ方の如何に関わらず、オレンジ色の各列において7の入り得る場所は★の3マスに限定されてしまう。
なので、×印のマスに7を入れることはできなくなる んです。
『数字xのn列ネット』はこんな性質を持っているんですね。

では、実例として図6を。
なんだかどこも数字が埋まりそうにないけれど、実は、『数字xのn列ネット』を使うことで★マスに7が入ることがわかるんです。
ちょっと確かめてみましょう。

数字7の入り得るマスをすべて挙げてみます。
すると、図7の通りになりました。★のあるマスに7が入り得ます。
そして、ピンク色の3列に注目しましょう。
なんと、よ〜く見ると 白い★の8マスが『数字7の3列ネット』になっている!

そうなると、図5で解説した通り、オレンジ色の3列において×印のマスには7が入れられなくなってしまうんです。
それを踏まえて紫色のヨコ列を見てみると……なんと、7の入れられるマスはひとつしかありません。
3.「どちらにしても……」法

さて、図9を。
なんだかどこにも数字が入りそうにないけれど、実は★マスに5が入ることがわかるんです。
なぜでしょう?
とりあえず、数字5の入り得るマスをすべて挙げてみましょう。

5の入り得るマスは図10の通りです。
★、▲、△のマスに5が入り得ますね。
ここで、右下ブロックに注目。★の3マスのどこかに必ず5が入ることに注意してください。
すると、何が言えるのか。
その3マスのどこに5が入ったとしても、▲と△の少なくとも一方には5が入れられない ということがわかるんです。

▲に5が入らない場合、赤色の列を見れば左上隅マスに5が確定する。
△に5が入らない場合、紫色の列を見れば左上隅マスに5が確定する。
どちらにしても、左上隅マス(図9の★マス)に5が入ることになるわけですね。

もう一例やってみましょう。
図12において、ピンク色の4マスにはどれも5か8のどちらかが入りますね。
そして、その4マスの位置関係を考えると、5と8は2つずつ入ることもわかります。それを▲と△で表しておきましょう。
「▲=5、△=8」or「▲=8、△=5」のどちらかになるというわけですね。
また、★マスに入り得る数字は2・5・8の3つです。
これも踏まえておきましょう。

今のところ、▲や△のどちらに5や8が入るかは確定できません。
しかし、★マスを含むタテヨコの列には▲も△も含んでいる。
実は、ここがミソ!

「▲=5、△=8」or「▲=8、△=5」のどちらにしても、▲と△の2マスには5も8も入ってしまうことが約束されているんですね。
だから、図13の★マスには5も8も入れられなくなってしまうんです。
もともと、★マスに入り得る数字は2・5・8の3つでした。
ということは、★マスに入れられる数字はただひとつ。
2が入ることになるわけです。
4.「巡り巡って……」法

図15を見てみましょう。
「あともう一息で完成!」というところまで来たものの、ここからがどうも先へ進めない。
しかし、こんな突破法があるんです。
まず、ピンク色ブロックの★マスに注目します。
★に入る数字は1か8のどちらかですね。これを頭の片隅に置いておいてください。

今、★を数字だと思って、他に★が入るマスを見つけていきましょう。
★からレーザー発射!
白色の★からスタートして、★→★→★ の順に見つかります。
(★のあるブロックすべてに1と8の両方がないことに注意してください)
ここで、中央ブロックの★に注目しましょう!
図15で解説した通り、★=1 or ★=8のどちらかになるんでした。
それを踏まえつつ、その★から左にたどっていくと……。

なんと、左端に1がある!
ということは、★=1ではない ということがわかります。
つまり、★=8となるわけで、4つの★マスにはすべて8が入ることになるわけです。
5.「浜田ロジック」

図18において、ピンク色の3マスには1か9が入りますね。
そして、その3マスの位置関係を考えて、とりあえず▲と△で表すことにしましょう。
「▲=1、△=9」or「▲=9、△=1」のどちらかになるというわけですね。
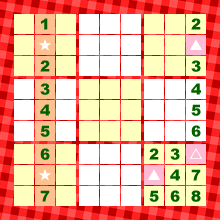
次に、オレンジ色の列に注目。
★の2マスには8か9のどちらかが入ることになります。
ところが、★の2マスから右にマスをたどっていくと……、なんと、ともに▲がある!
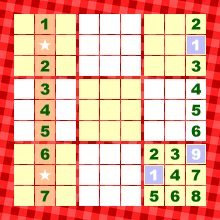
★マスの片方には必ず9が入るのだから、▲マスには9が入れられないことになりますね。
というわけで、▲=1、△=9となるわけです。
「浜田ロジック」という解法は、パズル作家・浜田剛先生によって発見された解法です。
余談ですが、浜田先生と管理人E坂は雑誌『ナンクロ』にて同時にパズル作家デビューを果たした仲だったりします。
浜田先生はこの「浜田ロジック」の発見などでも活躍がめざましいですが、さてアタシの方は……??