1.どういう解法?
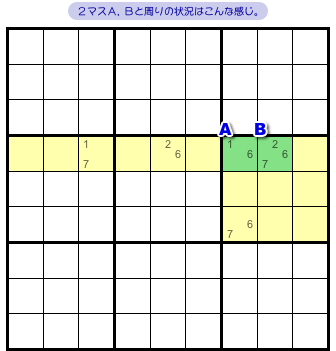
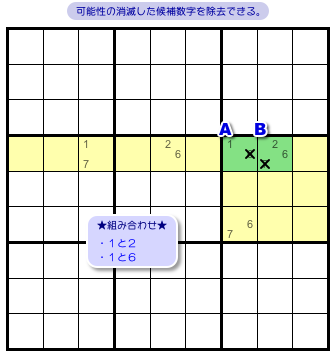
図1-1、緑色の2マスA, Bに注目しましょう。
そして、A, B両方の属する列とブロックも見てみます。
黄色部分で、マスは13個ありますね。
その中に、次の2つを満たすマスがチラホラあります。
- 候補数字を2個しか持っていない。
- その2個の内訳は、A, B両者の中から1個ずつ抽出したものである。
こんな感じの状況だったとしましょう。
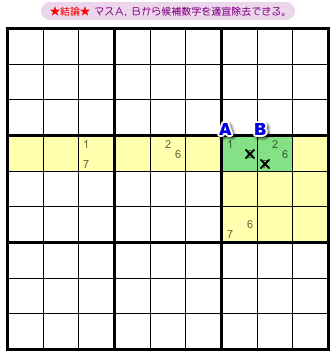
さて、図1-1 からはどういう結論が得られるんでしょう?
こうなります。
- 黄色マスの候補数字に応じて、2マスA, Bから候補数字を適宜除去できる。
前図1-1 の場合だと、マスA, B両方に候補数字の除去が起こります。
図1-2 の通りですね。
マスAから候補数字6を除去できます。
マスBから候補数字7を除去できます。
なぜ、こういう結論になるんでしょう?
以下で説明しましょう。
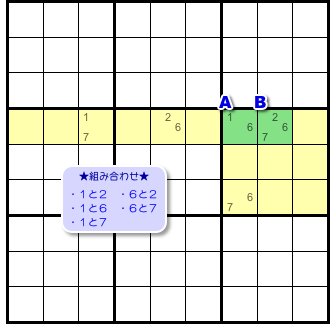
2マスA, Bの候補数字はそれぞれ2個と3個です。
ということは、単純に考えれば、この2マスに入る数字の組み合わせは2×3=6通りあるわけですね。
その6通りをちょいと列挙してみましょう。
- 1と2。
- 1と6。
- 1と7。
- 6と2。
- 6と6。
- 6と7。
あ、「6と6」がダメなのは明らかですね。
最初から除外しちゃいましょう。文字を薄くしておきます。
残った5通りのうちどれか1つが当てはまるわけですね。
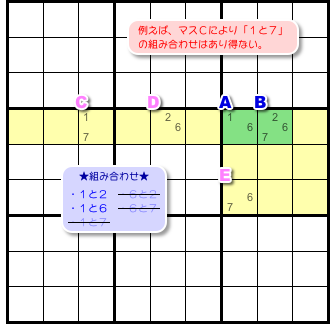
ところが!
実は、もっと除外できるんです。
例えば、マスCを見てみると「1と7」も除外できます。
なぜなら、「1と7」を採用したらマスCに入る数字が1つもなくなっちゃう😅
まだまだあります。
マスDを見ると「6と2」も除外できます。
マスEを見ると「6と7」も除外できます。
なんと、さらに3つも除外できる!
- 1と2。
- 1と6。
- 1と7。 ※マスCによりダメ
- 6と2。 ※マスDによりダメ
- 6と6。
- 6と7。 ※マスEによりダメ
たった2通りまで減ってしまいました。
さて、残った2通りから何が言えるんでしょう?
- 1と2。
- 1と6。
こういうことが言えるんです。
- マスAには数字1しか可能性がない。
- マスBには数字2, 6しか可能性がない。
なんと、マスA, Bに入り得ない数字が生じちゃったんです。
マスAに数字6の可能性はなくなった。
マスBに数字7の可能性はなくなった。
というわけで、結論はこうなります。
- マスAから候補数字6を除去できる。
- マスBから候補数字7を除去できる。
これが、図1-2 で示した結論です。
2.実際に使ってみよう!
次は、実際の盤面で Aligned Pair Exclusion を使ってみましょう。

図2-1 では、とあるマスから候補数字を除去できます。
それを解法 Aligned Pair Exclusion で突き止めてみます。
この解法を使うためには、ある列&ブロックを1個ずつ見つけ、その交差領域の2マスに注目しなければいけません。
列・ブロック・2マスを探しましょう!
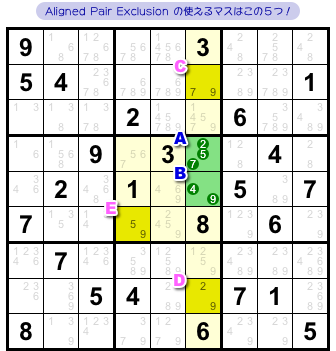
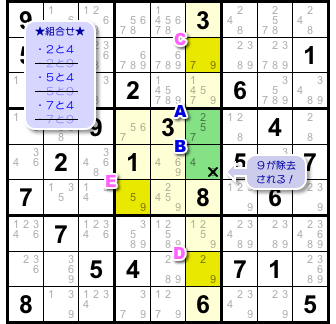
ここにありました!(図2-2)
2マスA, Bがあって、その周りには3マスC〜Eがある。
マスC〜Eはどれも次の2つを満たしています。
- 候補数字を2個持っている。
- その2個の内訳は、A, B両者の中から1個ずつ抽出したものである。
この5マスはこういう状況になっています。
ここから話が展開していきます!
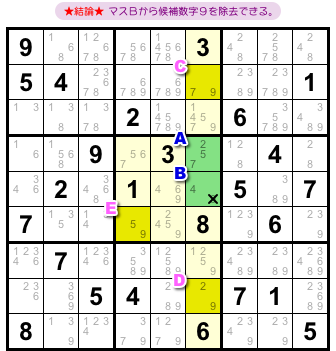
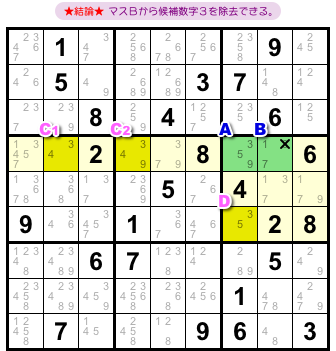
この場合の結論はこうなります。
- マスBから候補数字9を除去できる。
なぜでしょう?
それは、以下の解説により「マスBに数字9が入る」という可能性がなくなってしまうからです。
もちろん、3マスC〜Eが決め手となります。
では、解説していきましょう。
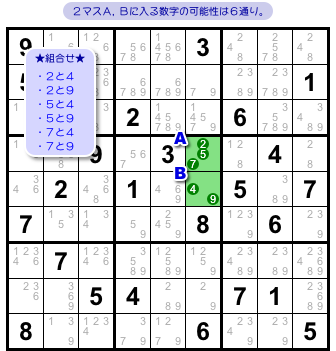
2マスA, Bに入り得る数字の組み合わせを列挙してみます。
以下の6通りですね。
- 2と4。
- 2と9。
- 5と4。
- 5と9。
- 7と4。
- 7と9。
しかし、マスC〜Eによって、この6通りのうちいくつかは除外されてしまいます。
例えば、マスCを見ると「7と9」は除外されますね。
D, Eを見ても同様に除外できます。
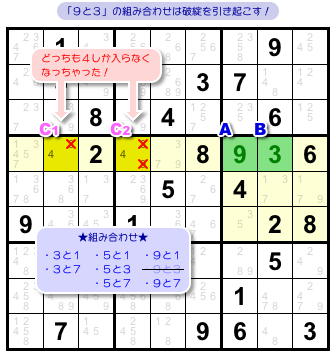
すると、組み合わせは3つに減りました。
- 2と4。
- 2と9。 ※マスDによりダメ
- 5と4。
- 5と9。 ※マスEによりダメ
- 7と4。
- 7と9。 ※マスCによりダメ
さて、残った組み合わせを見てみましょう。
なんと「9」が全部消えている!
マスBに数字9の入る可能性はなくなっちゃいました。
というわけで、マスBから候補数字9を除去できるんです。
図2-3 の結論通りですね😄
3.ALS を使った複雑なパターン
今までは、2マスA, B以外のマスは候補数字を2個しか持っていませんでした。
このセクションでは、A, B以外に Almost Locked Set(以下 ALS と略記)が登場するパターンを紹介します。
Aligned Pair Exclusion の拡張版です。
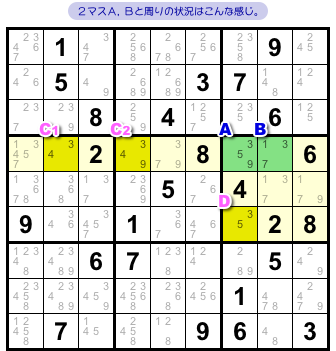
図3-1、2マスA, Bに注目しましょう。
そして、A, B両方の属する列とブロックも見てみます。
その中にめぼしいマスがいくつかありますね。
盤面はこういう状況になっています。
- A, B両者の属する列またはブロックには、候補数字を2個しか持たないマスがいくつかある。ALS がある場合もある。
候補数字を2個しか持たないのはマスDです。
C1, C2 からなる2マスが ALS です。
こういう状況の時、どういう結論が待っているんでしょうか?
こういう結論が待っています。
- マスBから候補数字3を除去できる。
では、解説していきましょう。
まずは、2マスA, Bに入る数字の組み合わせを列挙します。
- 3と1。
- 3と3。
- 3と7。
- 5と1。
- 5と3。
- 5と7。
- 9と1。
- 9と3。
- 9と7。
あ、もちろん「3と3」は最初からダメです。
全部で8通りですね。
ここから組み合わせがちょびちょび除外されていきます。
ALS(C1, C2)を見てみましょう。
候補数字は3, 4, 9ですね。
それを踏まえて、今度は前述の8通りの組み合わせに注目します。
3, 4, 9を使った組み合わせに「9と3」がありますね。
ちょっと試しに「9と3」を採用してみましょうか(図3-3)。
あっ!
C1 も C2 も4しか残ってない!
参ったなぁ。破綻してもぅた😣
実は、これは「9と3」だけに限りません。
ALS の候補数字をマスA, B両方に入れてしまうと、その ALS 内部で必ず破綻が起きてしまうんです。
3と4、3と9、4と3、4と9、9と3、9と4。
どれも破綻が待っている。
この6種類はすべてNGとなってしまいます。
前図3-2 の8通りの組み合わせのうち、このNGに該当するのは「9と3」ですね。
それを除外しちゃいましょう。
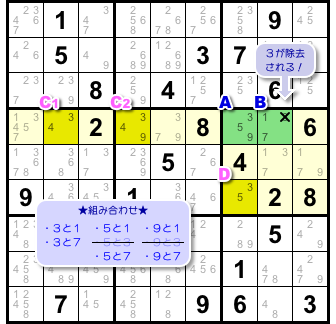
あと、マスDにより「5と3」も除外できますね。
結局、組み合わせは6通りに減りました。
- 3と1。
- 3と3。
- 3と7。
- 5と1。
- 5と3。 ※マスDによりダメ
- 5と7。
- 9と1。
- 9と3。 ※ALS(C1, C2)によりダメ
- 9と7。
この6つを見てみましょう。
あら、マスBに数字3の入る可能性がなくなっちゃった!
というわけで、マスBから候補数字3を除去できるのです。
図3-2 の結論通りですね😊
4.align してないのに Aligned?
今までのセクションでは、2マスA, Bはタテヨコ1列に並んでいましたね。
本来、Aligned Pair Exclusion は「一列に並んだ2マスの候補数字が除去される」という解法なんです。
なんたって「Aligned Pair」ですもんね。
ところが、とある事実が判明したんです。2マスは一列に並んでいなくても良いというのです!
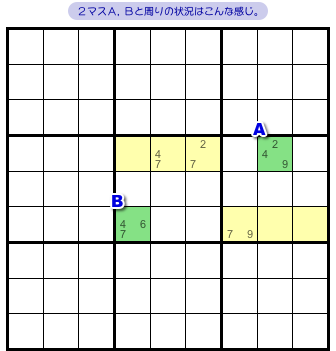
図4-1 の盤面にはマスA, Bがあります。
が、今までとは違ってタテヨコ1列に並んでいません。
なんと non-aligned pair ですね!
そして、マスA, B両方と列やブロックを共有しているマスがいくつかあります。
黄色部分で、6個ありますね。
その中に、次の2つを満たすマスがチラホラあります。
- 候補数字を2個しか持っていない。
- その2個の内訳は、A, B両者の中から1個ずつ抽出したものである。
こういう状況だったとしましょう。
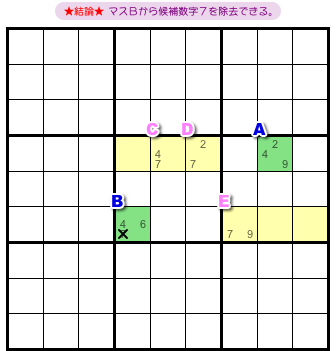
結論はこうなります。
- マスBから候補数字7を除去できる。
理由は同じです。
マスA, Bに入る数字の組み合わせは9通り。しかし、そこから3つを除外できるんですね。
- 2と4。
- 2と6。
- 2と7。 ※マスDによりダメ
- 4と4。
- 4と6。
- 4と7。 ※マスCによりダメ
- 9と4。
- 9と6。
- 9と7。 ※マスEによりダメ
残った組み合わせを見ると、マスBに数字7の入る可能性はなくなってしまいました。
こんなふうに、2マスが align(整列)していなくても同じ理屈が成り立っちゃう。
こういうパターンもあるんですね。
この場合の解法には固有の名前がついていないようですが、「Subset Exclusion」と呼ぶことがあります。
Subset Exclusion のページでは、実例も含めて解説しています。
更新履歴
- 2022. 2. 5.
- 新規公開。
- 2023. 3.31.
- ページ冒頭に難易度表記を追加。