1.こんな感じの解法です
X-Chain という解法は、リンクを使った解法です。
2マス間のリンクのみを使うため、リンクされる候補数字はたった1種類しかありません。
なので、Chain 系解法の中では X-Chain は最も簡単な解法です。
ただ、注意すべきことが1つある。
実は、リンクには「正しい使い方」があるんです。
その使い方に沿わないとリンクは役に立ってくれません。
X-Chain ではこのように使います。
- 複数の候補数字をリンクで数珠つなぎにし、枝分かれのない一本道を作る。
- 一本道の最初のリンクは 強いリンク とする。
- その次は 弱いリンク、そのまた次は 強いリンク、……と強弱のリンクを交互に連ねていく。
- 一本道の最後は 強いリンク とする。
つまり、強-弱-強-弱-…-弱-強 とリンクを連ねて一本道を作るというわけです。
強 に始まり 強 に終わる。
途中は強弱のサンドイッチ。
この一本道のことを チェーン と呼びます。
ま、文字だけじゃぁ何のことやらですよね😅
具体的な図で解説していくので、それを基に理解していってください。
以降、図の中には赤い矢印と青い矢印が現れますが、それぞれ 強いリンク と 弱いリンク を表します。
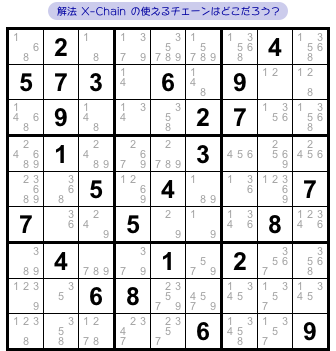
図1-1 の盤面で説明していきましょう。
X-Chain の使えるチェーンをこの盤面から作ってみます。
候補数字8のチェーンです。
さて、どんなチェーンができるんでしょう?
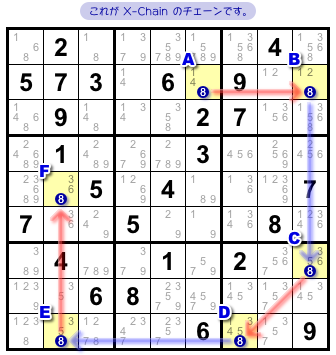
そのチェーンを作ってみました。
図1-2 の通りです。
マスAからFまで6個の候補数字8が5つのリンクで結ばれて、数珠つなぎになっていますね。
- 2マスA, Bの候補数字8は 強いリンク で結ばれている。
- 2マスB, Cの候補数字8は 弱いリンク で結ばれている。
- 2マスC, Dの候補数字8は 強いリンク で結ばれている。
- 2マスD, Eの候補数字8は 弱いリンク で結ばれている。
- 2マスE, Fの候補数字8は 強いリンク で結ばれている。
強いリンクで始まり、リンクが強弱交互に連なっていて、強いリンクで終わっていることを確認してみてください。
さて、こんなふうにチェーンができました。
このチェーン、どう役に立つんでしょう……?
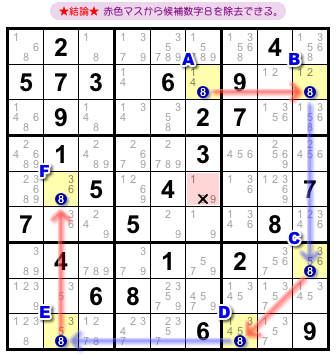
まずは結論を言いましょう。
こうなります。
- チェーン両端の2マスA, F両方と列を共有しているマスがある。そのマスから候補数字8を除去できる。
図1-3 だと、赤色マスが該当します。
赤色マスはAと同じタテ列に属し、Fと同じヨコ列に属しています。
その赤色マスから候補数字8を除去できるんです。
なぜこういう結論になるんでしょう?
それは、2マスA, Fの少なくとも一方に必ず数字8が入るからなんです。
それを解説しましょう。
ところで。
冒頭では「リンクは強弱交互に連ねる」と述べました。
実は、これが大きなカギを握っています!
チェーン先頭の候補数字に仮定を1つ与えると、強弱交互のリンク達は大きな大きな仕事をしてくれるんです。
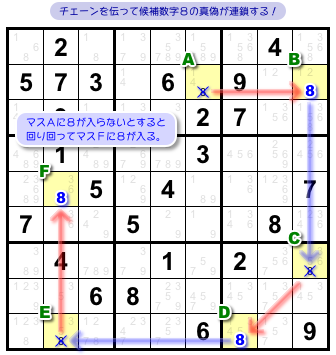
今、試しに「マスAに数字8は入らない」と仮定してみます。
すると、その仮定が引き金となって、チェーンに沿って怒涛の連鎖が起こるんです。
リンクは強弱交互。それが功を奏して、チェーン末尾のマスFまで光の速さで駆け抜ける!
- (仮定)マスAに8は入らない。
- すると、強いリンク によりマスBに8が入る。
- すると、弱いリンク によりマスCに8は入らない。
- すると、強いリンク によりマスDに8が入る。
- すると、弱いリンク によりマスEに8は入らない。
- すると、強いリンク によりマスFに8が入る。
仮定「マスAに8は入らない」から論理展開を始めたら「マスFに8が入る」に行き着いた。
というわけで、次のことが成り立つんです。
- マスAに8が入らない場合、必ずマスFに8が入る。
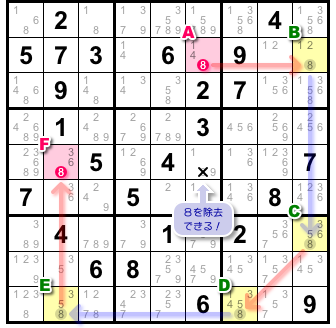
マスAに数字8が入らなければ必ずマスFに数字8が入る。
そうなると、数字8を入れられないマスが生じます。
2マスA, F両方と列を共有しているマスです。×印を付けています(図1-5)。
そのマスはAと同じタテ列に属し、Fと同じヨコ列に属しています。
マスAに数字8が入るか否か、どちらかが成り立ちますね。
8が入る場合、×印マスに8は入れられません。
8が入らない場合、代わりにマスFに8が入ります。この時も×印マスに8は入れられません。
結局、どちらにしても×印マスに数字8は入らないんです。
図1-3 の結論通りになりましたね😊
実は、図1-4 で述べた流れは大事です。
なぜかと言うと、これは Chain 系解法の本質部分でありキモだからです。
強弱交互に並んだリンク達に仮定を1つ加えたら、まるでドミノ倒しのように怒涛の連鎖が起こる。
X-Chain はもちろん、Alternate Inference Chain や Nice Loop などのマニアック解法でもこれを核として話が進むんです。
強いリンクと弱いリンクを交互につなぎ、チェーン先頭に仮定を1つ与える。
すると、リンクの道筋に沿って怒涛の論理展開が起こる。
このドミノ倒しのような展開を把握しておけば、Chain 系解法はさほど難しくはありません。
2.例をもうひとつ
前セクションでは、候補数字を除去できるマスは1つだけでした。
チェーン両端の位置関係によっては、複数のマスから候補数字を除去できることもあります。
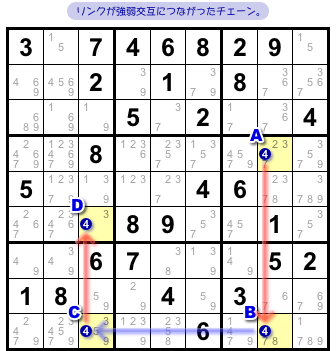
図2-1 の盤面には X-Chain の使えるチェーンがあります。
マスAからDまで、候補数字4のチェーンです。
至ってシンプルなチェーンですね。
- 2マスA, Bの候補数字4は 強いリンク で結ばれている。
- 2マスB, Cの候補数字4は 弱いリンク で結ばれている。
- 2マスC, Dの候補数字4は 強いリンク で結ばれている。
前セクション同様、リンクは強弱交互に連なっていますね。
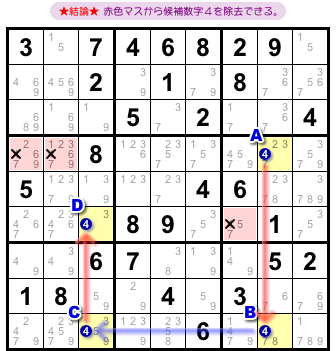
この場合の結論はこうなります。
- チェーン両端の2マスA, D両方と列やブロックを共有しているマスが複数ある。そのマスから候補数字4を除去できる。
図2-2 だと、赤色の3マスが該当します。
左の2マスはAとヨコ列を共有し、Dとブロックを共有している。
右の1マスはAとブロックを共有し、Dとヨコ列を共有している。
この3マスから候補数字4を除去できるんですね。
理由は前セクション1で展開した理屈と同じです。2マスA, Dの少なくとも一方に必ず数字4が入るからなんです。
一応、以下で解説しましょう。
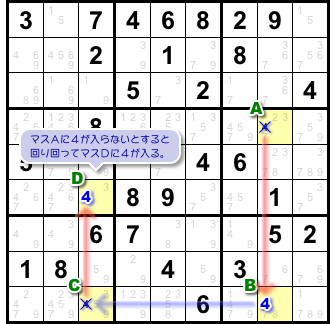
今、試しに「マスAに数字4は入らない」と仮定してみます。
すると、前セクション同様、チェーンに沿って連鎖が起こります。
- (仮定)マスAに4は入らない。
- すると、強いリンク によりマスBに4が入る。
- すると、弱いリンク によりマスCに4は入らない。
- すると、強いリンク によりマスDに4が入る。
マスAに4が入らないと仮定すると、回り回ってマスDに4が入る。
というわけで、次のことが成り立つんです。
- マスAに4が入らない場合、必ずマスDに4が入る。
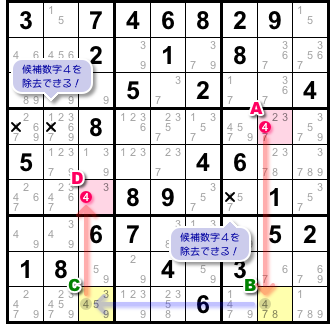
マスAに数字4が入らなければ必ずマスDに数字4が入る。
そうなると、数字4を入れられないマスが生じます。
2マスA, D両方と列やブロックを共有しているマスです。×印を付けています(図2-4)。
マスAには数字4が入るか否か、どちらかですね。
4が入る場合、×印マスに4は入れられません。
4が入らない場合、代わりにマスDに4が入ります。この時も×印マスに4は入れられません。
結局、どちらにしても×印マスに4は入らないんです。
図2-2 の結論通りになりましたね😊
前セクションとは違って、×印が複数生じることもあるんですね。
X-Chain の基本的な解説はここまでです。
以降は、特殊な場合を解説していきましょう。
3.グループリンクがある場合
チェーン内部にグループリンクがあっても、解法 X-Chain を使うことができます。
その場合を解説しましょう。
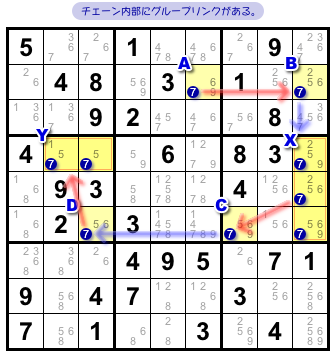
図3-1 には候補数字7のチェーンがあります。
内部に3つのグループリンクを持つチェーンですが、X-Chain が使える条件を満たしています。
ちゃんと強弱のリンクが交互に連なってますね。
- AとBは 強いリンク で結ばれている。
- BとXは 弱いグループリンク で結ばれている
- XとCは 強いグループリンク で結ばれている。
- CとDは 弱いリンク で結ばれている。
- DとYは 強いグループリンク で結ばれている。
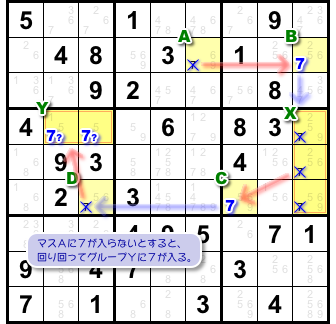
この場合も、今までとまったく同じ理屈が成り立ちます。
「マスAに7は入らない」と仮定してみましょう。
- (仮定)マスAに7は入らない。
- すると、強いリンク によりマスBに7が入る。
- すると、弱いグループリンク によりグループXに7は入らない。
- すると、強いグループリンク によりマスCに7が入る。
- すると、弱いリンク によりマスDに7は入らない。
- すると、強いグループリンク によりグループYに7が入る。
マスAに7が入らないと仮定すると、回り回って「グループYに必ず7が入る」という結果になりました。
- マスAに7が入らない場合、必ずグループYに7が入る。
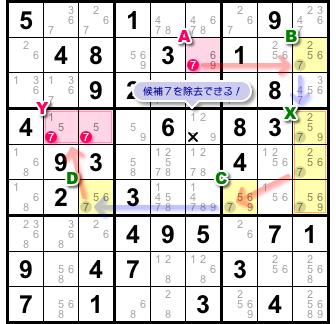
このことから、マスAとグループYの少なくとも一方に必ず7が入ることがわかります。
言い換えれば、図3-3 のピンク色3マスのうち最低1つに必ず数字7が入ります。
よって、×印マスから候補数字7を除去することができるんです。
4.チェーンがループした場合 (X-Cycle)
今までのセクションでは、チェーンの両端は同じ列にも同じブロックにも属していませんでした。
もし、両端が同じ列や同じブロックに属している場合はどうなるんでしょう?
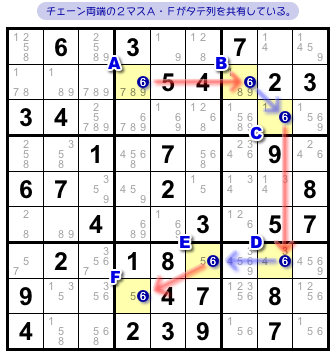
例えば、図4-1 のような形です。
チェーン両端は同じタテ列に属していますね。
チェーン両端が列やブロックを共有している場合、その両端同士を弱いリンクで結ぶことができます。
すると、強弱のリンクが交互に連なって一周し、チェーンがループ状になりますね。
実は、この形になると話が格段に複雑になっちゃう!
驚くような結論も得られます。
この解法は X-Cycle という名前でも知られており、ひとつの解法として確立しています。
詳細は X-Cycle のページで解説していますが、ここではとりあえず結論だけ示しましょう。
- 弱いリンクを含んでいる列やブロックにおいて、直接リンクされていないマスから候補数字6をすべて除去できる。
- 弱いリンクはすべて強いリンクに置き換わる。
更新履歴
- 2022. 2. 5.
- 新規公開。
- 2023. 3.31.
- ページ冒頭に難易度表記を追加。