1.チェーン表現もこれでスッキリ!
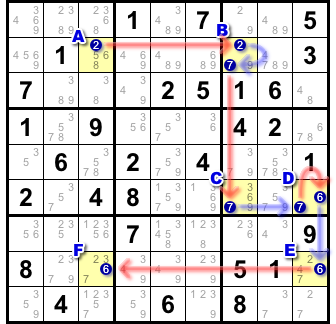
図1-1、これは Alternate Inference Chain で紹介したチェーンです。
マスAからFまで、7つのリンクでチェーンが構成されていますね。
そのチェーンの説明を書いてみます。
次のような感じになるでしょうか。
- マスA, Bは候補数字2の 強いリンク で結ばれている。
- マスB内部では候補数字2, 7が 弱いリンク で結ばれている。
- マスB, Cは候補数字7の 強いリンク で結ばれている。
- マスC, Dは候補数字7の 弱いリンク で結ばれている。
- マスD内部では候補数字7, 6が 強いリンク で結ばれている。
- マスD, Eは候補数字6の 弱いリンク で結ばれている
- マスE, Fは候補数字6の 強いリンク で結ばれている。
長い😅
ただただ長い😅
文章だと同じワードばっかり出まくるから、どうにもこうにも説明が長くなっちゃうんですよねぇ。
でも!
この長い説明、めちゃくちゃ短くできるんです。
図1-1 のチェーンをある表記法で表現すると……次のようになるんです。
- (2)r2c3 = (2-7)r2c7 = (7)r6c7 - (7=6)r6c9 - (6)r8c9 = (6)r8c3.
短い😊
めっちゃスッキリ😊
チェーンを説明する時は、こういう表現が簡潔で便利なんですね。
この表記法を Eureka notation と言います。
……まぁ、いくら簡潔だとは言っても、こんな数式みたいな字面を見てもサッパリわかんないですよね😅
次セクションでは、この表記を細かく解説していきましょう。
2.各要素はこんな意味
当然ですが、Eureka notation の中に現れている文字や記号が理解できないと Eureka notation は使いこなせません。
というわけで、このセクションでは各要素の意味を説明していきます。
前セクションで書いた Eureka notation をもう一度。
- (2)r2c3 = (2-7)r2c7 = (7)r6c7 - (7=6)r6c9 - (6)r8c9 = (6)r8c3.
これは3つの要素で構成されていますね。
r2c3 のような4文字、括弧書きの数字、イコールとマイナス。この3つです。
それぞれ解説していきましょう。

まずは、r2c3 とか r2c7 とかいう4文字表記。
これは何でしょう?
これは、マスを表します。
上から r1, r2, …… とヨコ列を表し、左から c1, c2, …… とタテ列を表していて、rとcの組み合わせでマスを表すんです。
例えば、図2-1 の黄色マスは r2c3 です。
また、複数のマスを一括表記できる場合があります。
例えば、同じ列にある青色3マスは r4c267 と表記します。
矩形状に並んだ緑色4マスは r69c58 と表記します。
ブロック内部のマスだと一括表記できない場合があります。
その時は、記号 | でつなげばOK!
例えば、左下ブロックの赤色3マスは r7c2|r89c3 と表記します。
記号 | のおかげで、どんな複数マスでも表記が可能です。
ちなみに、rは row、cは column の頭文字です。
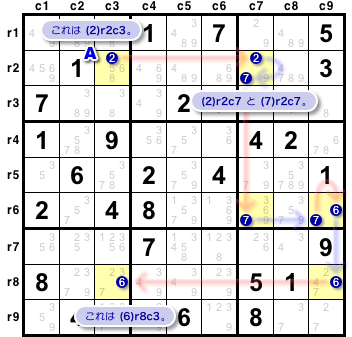
次に、マスの左に括弧書きの数字が書かれていますね。
(2)r2c3 の (2) です。
これは、候補数字を表します。
図2-2 で言うと、(2)r2c3 はマスAの候補数字2なんです。
- (2)r2c3 は「マス r2c3 の候補数字2」という意味。
他にも (2)r2c7 や (6)r8c3 などがあります。
図2-2 で示してみました。
あっ。
セクション冒頭の Eureka notation には (2-7)r2c7 や (7=6)r6c9 という表記もありますね。
それは別の意味を持っています。
詳しくは 図2-4 で説明しましょう。
最後は、イコールとマイナスです。
これはリンクを表します。
- イコール「=」は 強いリンク を表す。
- マイナス「-」は 弱いリンク を表す。
そういえば、リンクは強弱の他に2タイプありましたね。
2マス間のリンク、そして、マス内部のリンク。
それぞれについて説明しましょう。
まずは、2マス間のリンク。
これは簡単です。
単にマス同士をイコールやマイナスで結んで表記します。
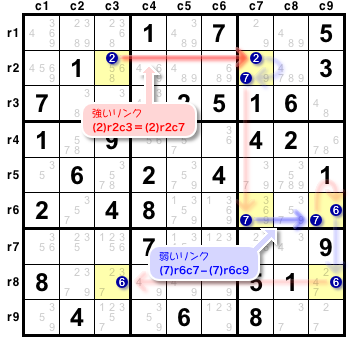
図2-3 で例を挙げましょう。
(2)r2c3=(2)r2c7 は「2マス r2c3, r2c7 の候補数字2は強いリンクで結ばれている」という意味です。
(7)r6c7-(7)r6c9 も同様で、候補数字7の弱いリンクです。

次は、マス内部のリンク。
これは少し特殊で、マス左側の括弧内で数字を結んで表記します。
図2-4 で例を2つ。
(2-7)r2c7 は「マス r2c7 では候補数字2, 7が弱いリンクで結ばれている」という意味です。
(7=6)r6c9 も同様で、マス r6c9 内部の強いリンクです。
以上を理解すれば、チェーンに対する Eureka notation 表記は理解できたと言って良いでしょう。
さっきの表記をもう一度。
- (2)r2c3 = (2-7)r2c7 = (7)r6c7 - (7=6)r6c9 - (6)r8c9 = (6)r8c3.
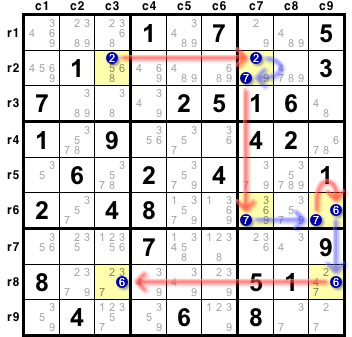
このチェーンの正体は 図2-5 です。
notation を追いながら確認してみてください。
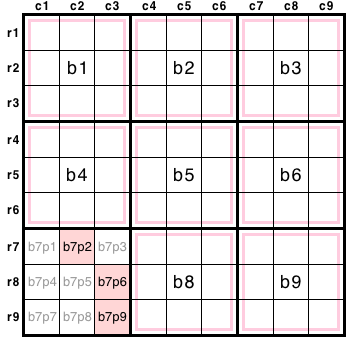
頻繁には現れませんが、ブロックに対する表現もあります。
左上ブロックを b1 として、順に b2, b3, …… で表します。
b124 などのように一括表記もできます。
また、ブロック内部の9マスは、左上を p1 として順に p2, p3, …… で表します。
このbとpの組み合わせでマスを表すんですね。
例えば、図2-1 の赤色3マスは r7c2|r89c3 と表せましたが、ブロック表記では b7p269 と表せます(図2-6)。
簡潔になった😊
ちなみに、bは box の頭文字です。
pは…… position とかかな?
3.結論も表記できる!
X-Chain などの解法では、チェーンのおかげで「該当マスから候補数字nを除去できる」などの結論が得られました。
実は、チェーンによる結論も Eureka notation で書くことができます。
このセクションでは、結論の書き方を解説します。
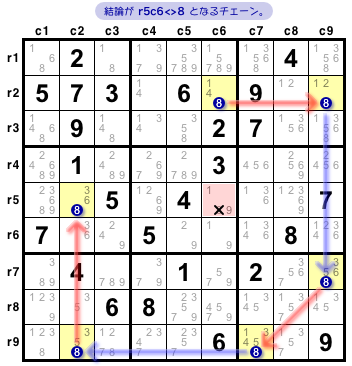
図3-1 は X-Chain のページで紹介した図です。
チェーンを Eureka notation で表してみましょう。
- (8)r2c6 = (8)r2c9 - (8)r7c9 = (8)r9c7 - (8)r9c2 = (8)r5c2.
このチェーンからは「赤色マスから候補数字8を除去できる」という結論が得られます。
実は、この結論も Eureka notation で書けるんです。
さてどう書くのか?
- (8)r2c6 = (8)r2c9 - (8)r7c9 = (8)r9c7 - (8)r9c2 = (8)r5c2 => r5c6<>8.
チェーンの後ろに「=>」を付けて、続けて結論を書く。
これでOKです。
「r5c6<>8」は「マス r5c6 に数字8は入らない」という意味を表します。
「ん? 結論は r5c6≠8 とは書かないの?」と疑問に思った方々は多いかもしれません。
たしかに、<> よりも ≠ を使う方が自然ですよね。
おそらく「≠」が全角文字であるというのが理由の1つかなと思います。
ナンプレに関する概念の多くは海外のフォーラムサイトなどで生まれました。
そして、文字化けなどの理由で、海外の方々は全角文字を扱いにくい。
そういう事情から、≠ を避けた可能性が考えられます。
……あるいは、BASICプログラムや Excel などからの流用かな?
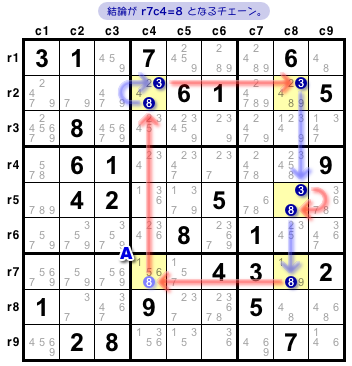
例をもう1つ。
今度は、Nice Loop(不連続ループ)で紹介したループです。
- (8)r7c4 = (8-3)r2c4 = (3)r2c8 - (3=8)r5c8 - (8)r7c8 = (8)r7c4.
このループからは「マスAに数字8が確定する」という結論が得られます。
Eureka notation で表すとこうなりますね。
- (8)r7c4 = (8-3)r2c4 = (3)r2c8 - (3=8)r5c8 - (8)r7c8 = (8)r7c4 => r7c4=8.
「r7c4=8」は「マス r7c4 に数字8が入る」という意味です。
強いリンクと混同しないよう、ご注意を!
ここまでの内容を理解すれば、Eureka notation の基礎を理解できたと言っても良いでしょう。
初歩的な Eureka notation の解読ができるようになります。
次セクションでは、複雑なチェーンの表記法について解説していきます。
4.複雑なチェーンの表現
簡単なチェーンなら前セクションまでを理解すればOKです。
しかし、チェーンにはグループリンクなど高難度なものも存在します。
このセクションでは、複雑なチェーンの表記法について解説していきます。
4-1.グループリンクがある場合
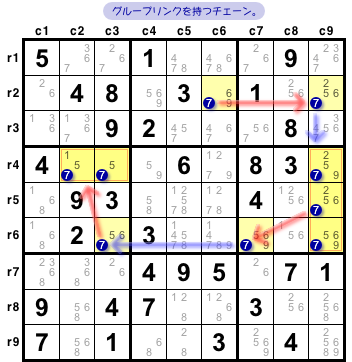
余談ですが、図4-1 のチェーンからは結論が1つ得られます。
それもちょっと書いておきましょう。
- (7)r2c6 = (7)r2c9 - (7)r456c9 = (7)r6c7 - (7)r6c3 = (7)r4c23 => r4c6<>7.
4-2.ALS がある場合
次は、さらに難しい物を。
チェーン内部に ALS がある場合です。
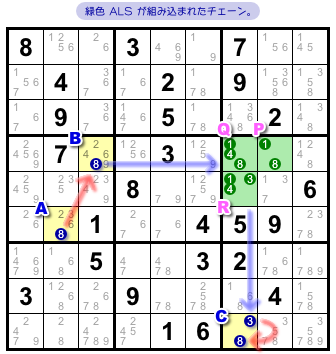
図4-2 を見てみましょう。
チェーン内部に3マスP, Q, Rの緑色 ALS が入っています。
実は、内部に ALS が組み込まれていてもチェーンとして機能することがあるんです。
図4-2 のチェーンだと、こう進んでいきます。
- (仮定)マスAに8は入らない。
- すると、強いリンク によりマスBに8が入る。
- すると、弱いグループリンク によりマスP, Qに8は入らず、この ALS は3国同盟に変化する。実際はP=1, Q=4, R=3 と立て続けに数字が確定する。
- R=3 と 弱いリンク によりマスCに数字3は入らない。
- すると、強いリンク によりマスCに数字8が入る。
このチェーン、Eureka notation ではどう書くんでしょう?
特に ALS 部分は気になりますね。
ここで、ALS について重要なことをおさらいします。
ALS は次の性質を持っています。
- 候補数字を1種類失うと、ALS はn国同盟に変化する。
Eureka notation では、この性質を利用した表記をするんです。

マス r4c3 と ALS は候補数字8の弱いリンクで結ばれてますね。
これは、ALS が候補数字8を失うと3国同盟(1, 3, 4の3国)に姿を変えるということを意味します。
このことを Eureka notation で表現するわけです。
- (8)r6c2 = (8)r4c3 - (8=143)r4c78|r5c7 - (3=8)r9c7.
太字の部分です。
括弧内の「143」が3国同盟を表しているんですね。
ここで注意が1つ。
1, 3, 4の3国同盟ですが、括弧内では「143」と表記されています。134 ではありません。
この理由は、緑色 ALS のすぐ後に候補数字3の弱いリンクが続いているためです。
直後にリンクが続く場合、その数字を括弧内の末尾に移してリンクをわかりやすく表記するんですね。
「3」を末尾に移して 134 を 143 とするんです。
余談ですが、このチェーンからも結論が得られます。
ついでに書いておきましょう。
- (8)r6c2 = (8)r4c3 - (8=143)r4c78|r5c7 - (3=8)r9c7 => r9c2<>8 => r9c2=2.
5.簡潔って素敵だね
ここからは余談です。
今まで見てきた通り、Eureka notation は簡潔に表せる画期的な表記法でしたね。
では、凄まじく長いチェーンでも Eureka notation はエレガントに短くなるんでしょうか?
ちょっと検証してみます。

図5-1 を見てみましょう。
うっわ、派手! 盤面がすっごく派手😅
マスAから始まり、チェーンが盤面を縦横無尽に駆け巡ってマスAに戻っています。
マス10個、リンク15個の長い長いチェーンです。
こんなにも長いチェーンだと、いくら Eureka notation といえども表現は長くなりそうですね。
ちょいと書いてみましょう。
- (8)r3c4 = (8-2)r3c8 = (2)r1c8 - (2=7)r1c1 - (7=6)r7c1 - (6)r9c3 = (6-1)r9c7 = (1)r4c7 - (1)r6c9 = (1-8)r6c4 = (8)r3c4.
あれ?
なんか思ったよりも長くなってない。
あ、いや、長いっちゃぁ長いんだけど、ビックリするほどではないなぁ。
まぁ、(8)r3c4 はたった7文字だし、(8-2)r3c8 は9文字ですもんね。
これらをイコールやマイナスでたくさんつないだところで、全体の文字数なんてたかが知れている。
事実、図5-1 の Eureka notation はたった 98文字でできているんです(ピリオドを含む)。
約100文字なんて、英語だと文くらいの短さです。文章ではなく重文や複文くらいの量。
その量でチェーン1本をまるごと表現できる。
本当に Eureka notation はエレガントなんですね。
有用な表記法だと言えます。
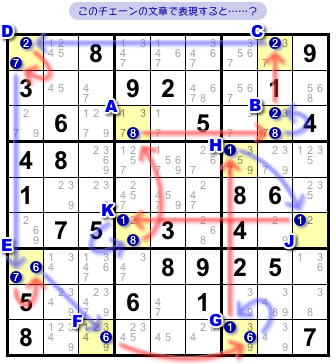
ついでに、前図5-1 のチェーンを文章で表してみましょうか。
- マスA, Bは候補数字8の強いリンクで結ばれている。
- マスB内部では候補数字8, 2が弱いリンクで結ばれている。
- マスB, Cは候補数字2の強いリンクで結ばれている。
- マスC, Dは候補数字2の弱いリンクで結ばれている。
- マスD内部では候補数字2, 7が強いリンクで結ばれている。
- マスD, Eは候補数字7の弱いリンクで結ばれている。
- マスE内部では候補数字7, 6が強いリンクで結ばれている。
- マスE, Fは候補数字6の弱いリンクで結ばれている。
- マスF, Gは候補数字6の強いリンクで結ばれている。
- マスG内部では候補数字6, 1が弱いリンクで結ばれている。
- マスG, Hは候補数字1の強いリンクで結ばれている。
- マスH, Jは候補数字1の弱いリンクで結ばれている。
- マスJ, Kは候補数字1の強いリンクで結ばれている。
- マスK内部では候補数字1, 8が弱いリンクで結ばれている。
- マスK, Aは候補数字8の強いリンクで結ばれている。
ぐわぁぁぁぁぁ〜!!
もぅもぅもぅ、見ただけで読む気が失せる😅
ちなみに、この15行は全390文字です。およそ原稿用紙1枚。
これを見ると、Eureka notation の優秀さが本当に際立ちますね。
やっぱり、「簡潔」というのは素晴らしいですね。
見やすい、読みやすい、頭に入りやすい、etc.
数学なんかでも「1に1を加えると2になる」よりも「1+1=2」の方が明らかにわかりやすい。
要点をしっかり押さえ、それをスパッと簡潔に書く。
すんなりと、そして正確に読み手に伝わる。
私はそういう文章に憧れを持っています。
そう書けるようになりたいものです。
……と言いつつ、私の解説ページがどれもこれも長すぎるのは何故なんでしょう?
簡潔になる気配がカケラもありません。
ボキャ貧だから?
文章力がないから?
文章構成がヘタクソだから?
他にも理由ある?
誰か、私に文章の何たるかを教えてください😅
ちなみに、図5-1 のチェーンからは結論が1つ得られます。
結論も書いておきましょう。
- (図5-1 のチェーン) => r3c4=8.
参考・参照
- Sudopedia(ミラーサイト), 『Eureka』,
http://sudopedia.enjoysudoku.com/Eureka.html
更新履歴
- 2022. 2. 5.
- 新規公開。
- 2023. 3.31.
- ページ冒頭に難易度表記を追加。