1.こんな感じの解法です
X-Chain では、チェーン両端の2マスを見て候補数字を除去することができました。
もし、偶数個のリンクが強弱交互に連なってループ状のチェーンになっている場合はどうなるんだろう?
このページでは、その場合の解法を解説していきます。
以降、図の中には赤い矢印と青い矢印がありますが、それぞれ 強いリンク と 弱いリンク を表します。
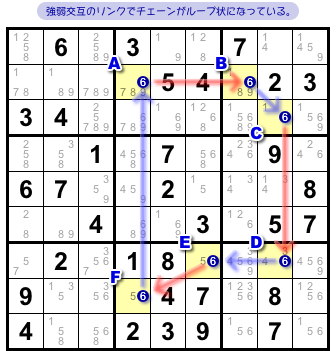
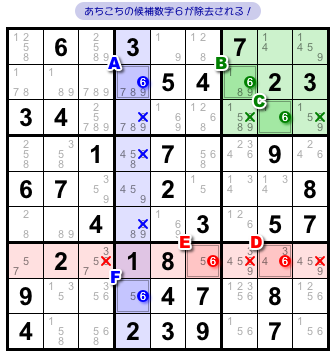
図1-1、マスA〜Fの候補数字6がリンクで結ばれています。
6個のリンクが強弱交互に連なって、ぐるっとループ状のチェーンができていますね。
X-Cycle は X-Chain の一種とみなすことができるので、X-Chain としての結論は当然成り立ちます。
しかし、それだけでは終わらない!
それをはるかに超えた深い深い結論が得られるんです。
んもぅ、あまりにも違う結論にビックリよ !?
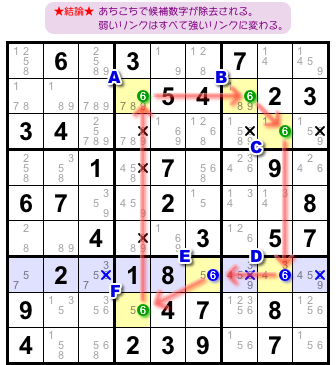
前図1-1 からはどんな結論が得られるんでしょう?
こうなります。
- 弱いリンクを含んでいる列やブロックにおいて、直接リンクされていないマスから候補数字6を除去できる。
- 弱いリンクはすべて強いリンクに置き換わる。
a. b. 成立後の盤面が 図1-2 です。
なんという変わりようだ!
チェーンは強くなるわ、候補数字はボロボロ除去されるわ(×印を付けてます)、何でこうなっちゃうの !?
a. がわかりづらいので、具体例をひとつ。
青色ヨコ列において2マスD, Eの候補数字6が弱いリンクで結ばれていましたが、その2マスにしか6の入る可能性がなくなるということです。他のマスから候補数字6を除去できます(青色×印)。
いや〜、ホント、すごい変わりようだ。
どうしてこうまで姿を変えてしまうのか?
それを解説しましょう。
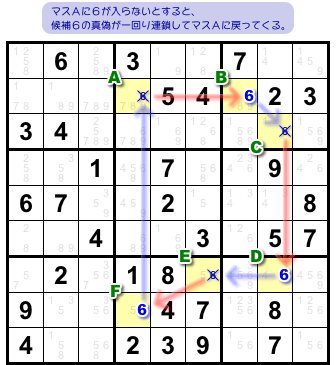
今、試しに「マスAに6は入らない」と仮定してみましょう。
すると、以下の通りチェーンに沿って連鎖していきます。そして矛盾なくマスAに戻ってきます。
- マスAに6は入らない。
- 強いリンク により、マスBに6が入る。
- 弱いリンク により、マスCに6は入らない。
- 強いリンク により、マスDに6が入る。
- 弱いリンク により、マスEに6は入らない。
- 強いリンク により、マスFに6が入る。
- 弱いリンク により、1. に戻る。
7. により、上記の手順は循環できます。
だから、どの番号から始めても一巡して同番号に戻ってくる。
これは、マスA〜Fのどこから始めても時計回りに論理展開できて、図1-3 と同じ結果に至るということなんです。
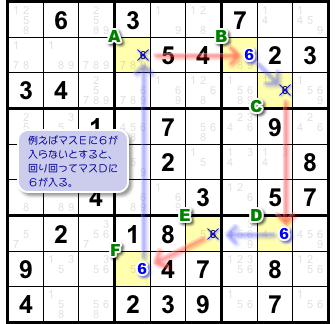
前図1-3 の手順 1.〜6. をたどると、次の結果が得られます。
- マスAに6が入らない場合、必ずマスFに6が入る。
これはマスAから話を進めた結果。
もちろん、チェーンはループ状なのだから、別のマスから始めることもできますね。
つまり、マスCやEから始めても時計回りに同じ論理展開ができる。
結局、全部で3つの結果が得られるんです。
- マスAに6が入らない場合、必ずマスFに6が入る。
- マスCに6が入らない場合、必ずマスBに6が入る。
- マスEに6が入らない場合、必ずマスDに6が入る。
マスAに数字6が入るか否か、どちらかが成り立ちます。
6が入るならそれで良し。
6が入らないなら、代わりにマスFに6が入ることになる。
ということは……? こうなるんです。
- 青色タテ列において、マスA, Fにしか数字6の入る可能性がなくなった。
というわけで、青色タテ列ではA, F以外のマスから候補数字6を除去できるんです(青色×印)。
2マスB, Cについても同様のことが言えます。
前図1-4 での説明により、緑色ブロックにおいてマスB, Cにしか数字6の入る可能性はなくなる。それ以外のマスから候補数字6を除去できます(緑色×印)。
2マスD, Eについても同様です。
赤色ヨコ列では、DとE以外のマスから候補数字6を除去できます(赤色×印)。
なんと、候補数字6を8つも除去できました!
これが 図1-2 の結論 a. なんです。
話はまだまだ続きます。
今度はリンクに変化が現れる!
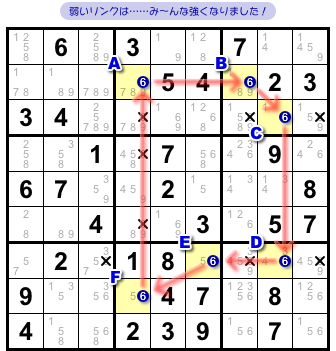
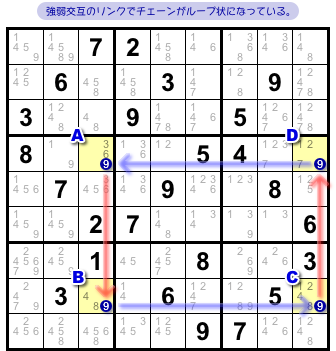
図1-4 では「マスAに6が入らない場合、必ずマスFに6が入る」と述べました。
このフレーズ、まさにこれを意味するんです。
- 2マスA, Fの候補数字6は強いリンクで結ばれる。
もともとA, Fを結んでいたのは候補数字6の弱いリンクでした。
しかし、強いリンクでも結ばれることになった。
つまり、弱いリンクを強いリンクに置き換えても良くなったんです。
同じ理由で、他の弱いリンクも強いリンクに置き換えできます。
なんと、一周ぐるっと全部強いリンクになっちゃった!(図1-6)
これが 図1-2 の結論 b. なんです。
ちょいと余談をひとつ。
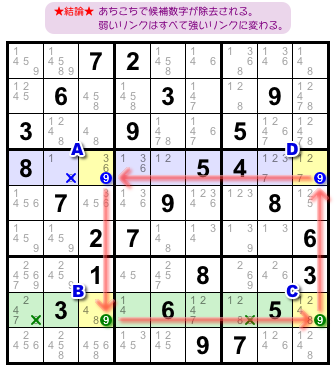
図1-2 で述べた結論 a. b. をもう一度書いてみます。
- 弱いリンクを含んでいる列やブロックにおいて、直接リンクされていないマスから候補数字6を除去できる。
- 弱いリンクはすべて強いリンクに置き換わる。
実は、この2つは本質的には同じです。
だから、必ずしも両方を覚える必要はないという……。
b. だけを覚えてしまえばラクかもしれませんね。
また、X-Cycle の一般形として Nice Loop(連続ループ)という解法があります。
Nice Loop では X-Cycle よりもさらに複雑な結論が得られます。
が、めっちゃムズい😅
本当に気が向いた時に読むことをオススメします。
2.例をもうひとつ
例をもうひとつ挙げましょう。
図2-1 の盤面には X-Cycle の使えるチェーンがあります。
今度は候補数字9のリンクからなるチェーンです。
矩形状で、至ってシンプルなチェーンですね。
この場合の結論はこうなります。
- 弱いリンクを含んでいるヨコ列において、直接リンクされていないマスから候補数字9を除去できる。
- 弱いリンクはすべて強いリンクに置き換わる。
a. b. 成立後の盤面が 図2-2 です。
これもまた、だいぶ変わりましたね!
チェーンは強くなり、候補数字9が3個除去されました(×印を付けてます)。
a. を具体的に言うと、こういうことです。
青色ヨコ列において2マスA, Dの候補数字9が弱いリンクで結ばれていましたが、その2マスにしか9の入る可能性がなくなるということです。他のマスから候補数字9を除去できます(青色×印)。
緑色ヨコ列も同様です。
B, C以外のマスから候補数字9を除去できます(緑色×印)。
どうしてこうなるんでしょう?
それを解説しましょう。
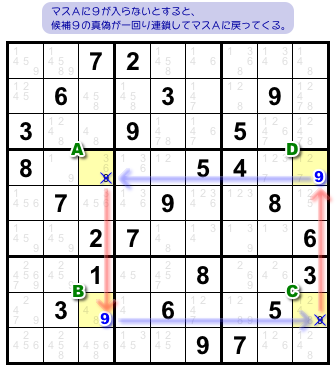
今、試しに「マスAに9は入らない」と仮定してみます。
すると、前セクション同様、以下の手順で話が展開して矛盾なくマスAに戻ってきます。
- マスAに9は入らない。
- 強いリンク により、マスBに9が入る。
- 弱いリンク により、マスCに9は入らない。
- 強いリンク により、マスDに9が入る。
- 弱いリンク により、1. に戻る。
上記の手順は循環できるので、どの番号から始めても一巡して同番号に戻ってきます。
マスA〜Dのどこから始めても反時計回りに論理展開できて 図2-3 と同じ結果に至るというわけですね。
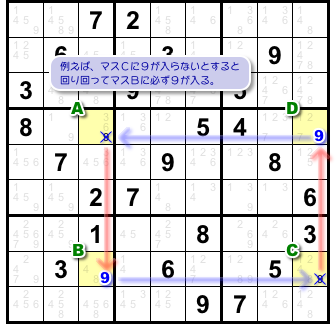
図2-3 の手順 1.〜4. をたどると、次の結果が得られます。
- マスAに9が入らない場合、必ずマスDに9が入る。
これはマスAから始めた結果です。
もちろん、同様に別のマスから始めることも可能ですね。
マスCから始めても同じ論理展開ができる。
結局、全部で2つの結果が得られます。
- マスAに9が入らない場合、必ずマスDに9が入る。
- マスCに9が入らない場合、必ずマスBに9が入る。
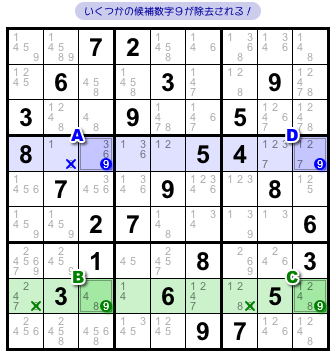
マスAに数字9が入るか否か、どちらかが成り立ちます。
9が入るならそれで良し。
9が入らないなら、代わりにマスDに9が入ることになる。
というわけで……、
- 青色ヨコ列において、マスA, Dにしか数字9の入る可能性がなくなった。
青色ヨコ列では、A, D以外のマスから候補数字9を除去できますね(青色×印)。
2マスB, Cについても同様です。
緑色ヨコ列において9の入り得るマスはB, Cの2つに限定され、それ以外のマスから候補数字9を除去できます(緑色×印)。
候補数字9を3つ除去できました!
これが 図2-2 の結論 a. なんです😊
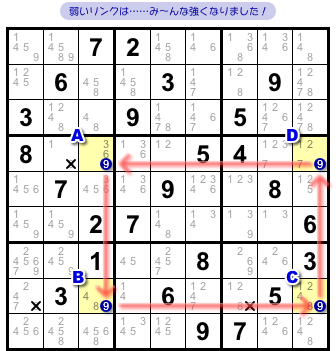
もうひとつ別の話。
図2-4 では「マスAに9が入らない場合、必ずマスDに9が入る」ということがわかりました。
つまり、こういうことが言えるわけですね。
- 2マスA, Dの候補数字9は強いリンクで結ばれる。
もともとA, Dを結んでいたのは弱いリンクでした。
しかし、強いリンクでも結ばれることになった。
つまり、弱いリンクを強いリンクに置き換えても良くなったんです。
同じ理由で、BとCを結んでいる弱いリンクも強いリンクに置き換えできます。
なんと、一周ぐるっと全部強いリンクになっちゃいました!(図2-6)
図2-2 の b. ですね😊
こうして見ると、リンク達のパワーには言葉も出ないですね。
チェーン状でも伝達力がすごいのに、ループ状になるとループ自身がパワーアップして盤面の候補数字をバッサバッサと斬りまくる!
ひとたび X-Cycle を見つけると、あまりの効率の良さに驚きを隠せません。
ただ、X-Cycle のパワーを堪能するのは非常にレアなんです。
チェーンを見つけるだけでも大変なのに、強-弱-強-弱-… とリンクをつなげて元に戻ってこなければいけませんからね。
ひとたび X-Cycle を見つけようとすると、あまりの見つからなさに驚きを隠せません😅
X-Cycle が見つかるのは宝くじに当たるのと同じことだ、と言っても過言ではない!
すいません😅
過言でした😅
3.X-Wing は X-Cycle の一種
ここからは余談です。
X-Wing と X-Cycle の関係について、ちょいと話をしてみます。
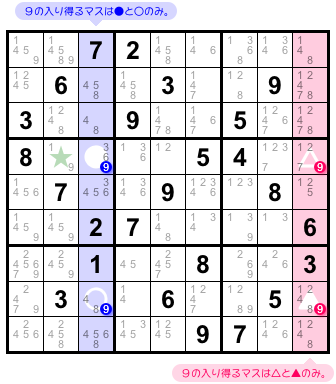
図2-1 の盤面、実は、X-Wing のページで実例として挙げたものと同じなんです。
X-Wing では候補数字9が矩形状に並んでいることに注目して解き進めましたが、X-Cycle では強弱のリンクを使って解き進めました。
こういうふうに、盤面によっては異なるアプローチで解き進められることがあるんですね。
実は、X-Wing は X-Cycle の一種とみなせるんです。
青色タテ列の●と○は候補数字9の強いリンクで結ばれていると言えるし、ピンク色タテ列の▲と△も候補数字9の強いリンクで結ばれていると言えます。
そして、ヨコ列を共有している●と△は候補数字9の弱いリンクで結ばれているし、○と▲も同様です。
この4つのリンクで矩形状のループができたわけですね。
X-Wing でも X-Cycle でも「★マスに1が確定する」という同じ流れで解けていきますが、解き進め方の理屈や視点が異なっているのが面白いですね。
ナンプレにはたくさんの上級解法がありますが、それらの一部はリンクやチェーンを使って説明することが可能です。
Skyscraper、2-String Kite、Remote Pair などは X-Chain の解法で説明することもできます。
チェーンは汎用性の高い概念なんですね。
更新履歴
- 2022. 2. 5.
- 新規公開。
- 2023. 3.31.
- ページ冒頭に難易度表記を追加。